Интегральная модель ориентирована на тот слу­чай, когда процесс массообмена между фазами протекает само­произвольно вследствие разности между рабочими и равно­весными концентрациями вещества в каждой точке объема аппарата.

Сложности формирования поверхности межфазного взаимо­действия, особенности гидродинамики течения для каждого ти­па массообменного аппарата концентрируются в коэффициенте массоотдачи. Его определяют, обобщая экспериментальные дан-

Ные уравнениями массопередачи, которые представим для двух­фазных систем на базе модели 0 межфазной турбулентности в форме

А,

К I / Т£) I т ‘'ОЛТ ______ ^ 1

= (1+/); (10.13)

)"' (1 + /). (Ю.14)

Где } — фактор гидродинамического состояния двухфазной си­стемы; г, ж — индексы газовой (паровой) и жидкой фаз.

При 1 = 0 уравнения (10.13), (10.14) переходят в уравнения массопередачи, получаемые из пленочной теории массообмена в двухфазных системах. Тогда количество вещества для газовой фазы, переносимое из элемента объема через поверхность получим из уравнения

ЙМ = Коу{у — уР)йР. (10.15)

Аналогично для жидкой фазы

ЙМ = Кох (*р — х) йР. (10.16)

Равновесные концентрации и линии фазового равновесия.

В двухфазных системах в результате массообмена за бесконеч­ное время наступает термодинамическое равновесие. Равновес­ное состояние системы определяется согласно правилу фаз Л/+Ф = к + 2 (10.17), где /V — число степеней свободы; Ф — число фаз; к — число компонентов.

В качестве параметров обычно фиксируются концентрация компонента в жидкой фазе х, парциальное давление над жид­костью Р и температура

При анализе двухфазных систем с двумя компонентами в качестве параметров могут быть выбраны следующие: х— со­держание низкокипящего компонента жидкости; Р — парциаль­ное давление; х, I — температура; у, х — содержание низкоки­пящего компонента в паре и в жидкости. Соответственно равно­весные соотношения представляются в графиках х—р; х— у—х.

При малой концентрации распределяемого компонента связь между параметрами Р и х определяем по закону Генри:

УР = ^хА, (10.18)

Где ф — константа Генри; Р — полное давление в системе; ха— содержание распределяемого компонента А в жидкой фазе; ур — равновесное содержание того же компонента в газовой (паровой) фазе. Значение константы Генри зависит от свойств газа, жидко­сти и температуры.

Рассматриваются идеальные системы, для которых справедлив закон Рауля. Этот закон устанавливает линейную связь между содержанием летучего компонента в жидкости, находящейся в равновесии с паром, и его парциальной упругостью: Р = = ха. Ра (10.19), где Р — парциальное давление компонента над смесью; хА—молярная доля компонента в жидкости; рА—давле­ние паров индивидуального компонента А.

Следуя выкладкам [34], получаем уравнение для равновесной концентрации компонента в газовой (паровой) фазе:

•ь-ТП^ТУТГ' (10'20)

Где а — относительная летучесть компонента А,

А = Ра/Рб - (10.21)

Здесь ра, Рв — упругость паров компонентов А и В. В — труд­нолетучий компонент. Уравнение (10.20) используется для пост­роения диаграммы равновесия. Если в равновесии находятся фазы, для которых законы идеальных газов и идеальных жид­костей не действительны, то равновесные концентрации г/р=: = f(x) определяются экспериментально или по справочной ли­тературе.

Рабочая концентрация и линии рабочих концентраций. На­чальные и конечные концентрации компонентов в фазовых по­токах бывают заданы. Заданные и фактические концентрации фазовых потоков в аппаратах называются рабочими концент­рациями. Рабочие концентрации распределяемого вещества не равны равновесным и в действующих аппаратах никогда не достигают равновесных значений.

Зависимость между рабочими концентрациями y=f(x) на­зывается рабочей линией процесса. Вид функции y=f(x) для всех массообменных аппаратов получается из уравнений мате­риального баланса.

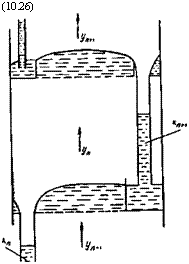
Пусть в аппарат (рис. 10.2) сверху поступает Lsl, а снизу

Отводится LK жидкой фазы с массовым содержанием компонен­

Та А, соответственноравным ха и хк. Газовая фаза G„ поступает снизу и отводится сверху G* е массовым содержанием компо­нента А, соответственно равным у„ и ук.

Запишем условия материального баланса по всему вещест­ву и данному компоненту для аппарата:

GH + L„ = GK - j - Z. K; (10.22)

Gut/.I + LuxH = GKyK -)- LKXn. (10.23)

Представим уравнения баланса всего вещества и компонента А для некоторого сечения аппарата:

0„ + /. = 0+£к; (10.24)

(*нУн --Ьх = йу + (10.25)

Из последнего получим уравнение - рабочей линии

(10.26)

I — внУн — 1кдгк

У = тх

«<А

Рис. 10.2. Схема потоков в ректификационной колонне

Рис. 10,Зі. Схема тарельчатого элемента ректификационной колонны

Выражающее связь между рабочими концентрациями распреде­ляемого компонента в произвольном сечении аппарата. Если расходы фаз постоянны по высоте аппарата, рабочая линия — прямая.

Средняя движущая сила процесса переноса и число единиц переноса. Отклонение состояния вещества от состояния равно­весия характеризуется разностью равновесной и рабочей кон­центраций компонента в одной фазе. Разности концентраций Аг/р и Длгр определяют процесс массопередачи и представляют собой движущую силу процесса.

Запишем уравнение материального баланса в элементе ап­парата высотой с1„ с поверхностью фазового контакта с! Р, в ко­тором изменение материального потока вещества по высоте при­равнивается к диффузионному потоку через поверхность:

ЙМ = — вс{у = К1/(у — У?)йР. (10.27)

Разделив переменные и выполнив интегрирование, получим

К/ г _йу_. (10 28)

0 3 у-ур

Ук

Так как М — С(уи— г/к), то из уравнения (10.28) найдем

М = КуР-Ун-~-'к = К^ьГу. (10.29)

Ун

1-2

<1у

Ур

Н

При линейной зависимости равновесных концентраций сред­нюю движущую силу процесса по высоте противоточного аппарата определим как среднелогарифмическую [31]. Когда рабочая лнния лежит выше линии равновесия, имеем

(Уп ~ Упр) ~ {У(п—1) У(п - 1)р)

П р

У ~ ---- у „—упт, : (10.30)

2,318

У(п-1) — У(п-1)р

(*(ге+1)р хп+) ~ (*пр хп)

Аа:— ‘ .(Ю.31)

2,31я-("+1)р П+1

Хпр ~ *п

Ин аче

- (Упр Уп) (У(п - 1)р У[п-])) .

УПр-уп > (Ю.32)

’ % У(П-1)Р-УП-Х

- (жя+1 Лл+Пр)- (ХП~ хпр)

Дл: = :—х------ ГГТ---------- • (10.33)

2,31

Хп хпр

Выражения для средней движущей силы, когда рабочая линия процесса в аппаратах промежуточного типа ниже равновесной, имеют вид

Уп — Уп-1

АУ = ------------------ Уп ~Уп 1 (10,34 )

2.3

Е Уп р — Уп

Й ----------- -+1 . (10.35)

2.3 ]8 _2±! 122.

Хп — *пр

Рассмотрим некоторый элемент массообменного аппарата (рис. 10.3).

Примем, что жидкость на вышележащей тарелке имеет конеч­ную концентрацию хл+|. На нижележащей тарелке эта концент­рация изменяется до хп. Пар, поступающий на нижнюю тарелку, имеет концентрацию ул_х и изменяется до уп.

Если расхвд пара С, то количество вещества, переходящего из

Одной фазы в другую, определяется из уравнения

М = в(уп — уп-). (10.36)

Это же количество распределяемого между фазами компонента может быть записано е виде (10.29): М — КуРАу. Принимая, что р = аУт, где Ут — объем жидкости на тарелке, м3; а — удельная поверхность фазового контакта, м2/м3, получаем

М = К„УпЬу. (10.37)

Сопоставляя уравнения (10.36), (10.37), находим

(10.38)

__ Уп Уп—1 _____ Куу^т

I/

Д у С,

Соотношение (10.38) называется числом единиц переноса и пред­ставляет собой отношение изменения рабочих концентраций к сред­ней движущей силе.

Если принять ^ = 6/^ (/„ — рабочая площадь сечения тарелки, м2; Ь — удельная поверхность фазового контакта, м2/м2), то урав­нение для определения количества компонента, переходящего из одной фазы в другую, можно записать в виде

М = КиЬ}тЬу = КЛтЬу. (10.39)

Тогда число единиц переноса

Уп Уп~

Щт=~Ту----------- = (Ю.40)

Используя выражения (10.34), (10.35) для аппаратов смешан­ного типа, выражения для числа единиц переноса запишем так:

Упр Уп—I Тп Хп+1 Хпу

Т

Ут

Тхт = 2,3 ]ё (Ю 42) Хпр Связь между коэффициентами массопередачи и массоотдачи. Процесс массопередачи включает в себя массоотдачу в пределах каждой из взаимодействующих фаз и перенос распределяемого вещества через границу (поверхность) раздела фаз. Поэтому Уравнение массопередачи для конечного элемента имеет вид М (д — (10.43); М = К, (хр - х) Р. (10.44)

- 2.318 ; (10.41) Упр Уп

Если концентрации фаз изменяются при движении вдоль по­верхности раздела, уравнение (10.43) записывается в форме (10.29). Аналогично можно представить и уравнение (10.44).

Допустим, что распределяемое вещество переходит из паро­вой фазы в жидкую и движущая сила выражается в концентра­циях паровой фазы, тогда количество вещества, переходящее из фазы в фазу, определяется уравнением (10.43).

Ввиду сложности механизма массоотдачи в объеме фазы при­нимают

М = РУР(у — угр) (10.45); М = $ХР (хгр — х), (10.46)

Где у, Угр — концентрации компонента соответственно в ядре и на границе паровой фазы; х, хгр — то же для жидкой фазы.

Чтобы установить связь между коэффициентами массоотдачи

(3* и коэффициентами массопередачи Ку и Кх, принимают, что на границе раздела фаз достигается равновесие. Это значит, что сопротивлением переноса через границу можно пренебречь.

Рассмотрим случай, когда равновесная зависимость линейна, т. е. ур = тх. Тогда с учетом принятых допущений

М = Уг—~. (Ю.47)

Или Из уравнения (10.46) имеем

Мт

Утр Ур р р • (10.48)

У-Уг (10-49)

Сложив соотношения (10.49) и (10.48), получим

Y-^=-r(j;+ j;)' (10-50)

Подставив уравнение (10.50) в (10.43), найдем

1 г- + -5—. (Ю.51)

Аналогично запишем

Г. Г,

— = —4--J—. (10.52)

H hm

При криволинейной зависимости yP=f(x) величина m изменя­ется по высоте аппарата и, следовательно, изменяется коэффи­циент массопередачи. В этом случае всю область разбивают на участки, в пределах которых m постоянно, и для аппарата зада­ют разные значения К-

Состав фаз, способы выражения состава. Фазовые потоки в массообменных аппаратах представляют собой смеси двух и боль­шего количества компонентов. Если смесь состоит из компонентов А, В,. N, молекулярные массы которых Мл, М_в, ^ Мц и массовые доли ха, хв, ■ •> хы для каждой фазы и ул, Ув, ■ ■

У.' Дл НЫ

*і/ м< іш*А Ук/ МК

N

Паровой фазы ук =

Для

N V Массовое содержание любого компо­нента на ходим из соотношений

Я паровой фазы, то содержание любого компонента в моль- Долях определяем по следующим уравнениям: *к/ Ч Чля жидкои фазы хк

Рис. 11.1. Схема ректификаци­онной установки непрерывного действ ия: 1 — дефлегматор; 2 — колонна; 3 — кипятильник

Ректификационные установки предназначены для раз­деления жидких смесей на практи­чески чистые компоненты или фрак­ции, различающиеся температурой кипения. Физическая сущность про­цесса ректификации заключается в двухстороннем массо - и теп­лообмене между неравновесными потоками пара и жидкости. При контакте паров смеси с жидкой смесью, вследствие то­го что температура паров смеси выше температуры кипения низ - кокипящего компонента, но ниже высококипящего, происходит испарение из жидкой смеси низкокипящего компонента и кон­денсация из паровой смеси высококипящего компонента. В ре­зультате многократного повторения массообмена пар обогаща­ется низкокипящим компонентом, а жидкость — высококипящим. Ректификационные установки включают ряд теплообменных аппаратов для подготовки рабочего процесса, вспомогательное оборудование и ректификационную колонну (рис. 11.1), в ко­торой осуществляется процесс ректификации.

Опубликовано в Теплонспользующие установки промышленных предприятий « МАТЕРИАЛЫ, ПРИМЕНЯЕМЫЕ ДЛЯ ШТАМПОВКИ. ЛИСТВОЙ ПРОКАТ. СОРТАМЕНТ Особенности конструктивного решения ректификационных колонн » Комментарии закрыты. Новые материалы: Рекомендации по выбору бизнеса, как на основе нашего оборудования, так и без Где работают наши линии по производству пенопласта Оборудование и технологии производства полистиролбетона Оборудование для производства пенобетона. Ком. предложение Рубрики: Линии по производству Оборудование для изготовления Разное Техническая литература Новости Лидеры производства Станок МАРС (производство шлакоблоков) Паровой комплекс (котельная) на основе РИ-5М (самый дешевый источник пара) Мини-заводы по производству пенополистирола (пенопласта) и термоблоков Мини-заводы по производству пенобетона, влагостойкие формы для пенобетона Контакты: Производство хонголовок +38 050 4571330 msd@msd.com.ua Информация Copyright © Мастерская своего дела