Гидравлическая, тепловая и пневматическая модели инерцион­ных (апериодических) звеньев приведены на рис. 9, электрические — на рис. 17, а. Все эти модели элементарных звеньев имеют одинаковые временные и частотные характеристики. Рассмотрим электрическое инерционное звено. Входной величиной электрического инерционно­го звена является напряжение vBX, а выходной ипых. Ток заряда кон­денсатора /с зависит от величины возмущения UBX и сопротивления

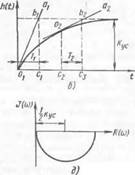
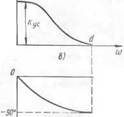
Рис. 17. Инерционное звено:

с—-пример электрического инерционного звена и диаграмма прохожде­ния сигналов, б — временная характеристика, в — АЧХ. г — ФЧХ,

R. Величина тока /с, протекающего через конденсатор С, и время за­ряда конденсатора / определяют величину заряда конденсатора Q, от которой, в свою очередь, зависят напряжение на обкладках конден­сатора Uных и сопротивление конденсатора Rc постоянному току. С увеличением сопротивления конденсатора Rc уменьшается ток заряда конденсатора /с-

Для всех инерционных звеньев диаграмма прохождения сигнала имеет отрицательную обратную связь, т. е. для них характерно само - выравнивание. Основной отличительной особенностью инерционного звена от остальных типовых элементарных звеньев является наличие отрицательной обратной связи.

Временная характеристика инерционного звена была рассмотрена в§ 11. Если к кривой h(t) (рис. 17,6) инерционного звена провести касательную к любой ее точке, то расстояния от проекции точки ка­сания на ось времени до проекций точки пересечения касательной с продолжением установившегося значения h(oo) равны между собой независимо от того, к какой точке временной характеристики прове­дена касательная.

На рис. 17, б касательные огах и Офг проведены к двум точкам ох и oz. Проекции отрезков касательных охЬг и о2Ь2 на ось времени t {охсх

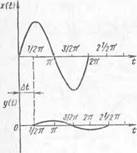
Рис. 18. Предельный сдвиг инерционного звена

и с2с3) называются постоянной времени, обозначаются Т и измеряются в едини­цах времени. Особенность временной характеристики инерционного звена заключается в том, что независимо от того, к какой точке характеристики про­ведены касательные, проекция касатель­ной на ось времени остается постоян­ной, т. е. в нашем примере 7 = Т2. Кривые, у которых проекция касатель­ной (для любой точки касания) — ве­личина постоянная, называются экспо­нентами.

Установившееся значение временной | характеристики Л(оо) называется коэф­фициентом усиления звена и обознача­ется кус.

Частотные характеристики инерци­онного звена имеют специфические от­личительные особенности по сравнению с другими типовыми звень­ями. Значение АЧХ звена (рис. 17, в) при нулевой частоте равно коэффициенту усиления звена /4(со0) = кус. С увеличением частоты колебаний при постоянной амплитуде входных периодических колеба ний амплитуда выходных колебаний звена уменьшается и при неко­торой частоте становится равной нулю. Поэтому ординаты кривой АЧХ инерционного звена с увеличением частоты уменьшаются до пересечения с осью абсцисс (точка d). Частота, при которой колеба­ния на выходе звена уже не могут быть измерены, называется часто­той среза звена (оср, т. е. Л((оср) ss 0. Принято говорить: все частоты, больше частоты соср, звено отфильтровывает.

Характерная особенность ФЧХ инерционного звена (рис. 17, г) заключается в том, что максимальный угол сдвига — <?(«>) стремится к 90а, но никогда его не превышает. Сдвиг 90е соответствует 1/4 перио-| да периодических колебаний, так как полный период составляет 360°, сдвиг 90® = 1/2п.

На рис. 18 приведены периодические колебания входа x{t) и выхо­да yit) при частоте, близкой к частоте среза. При относительном сдви - геД*= V2ji амплитуда выхода равна нулю.

АФЧХ звена представляет полуокружность (см. рис. 17, д), про­веденную радиусом кус/2,‘с центром, лежащим на вещественной оси и отстоящим от начала координат на величину У. г кус, где кус• — ко­эффициент усиления звена при нулевой частоте.