ГОРЕНИЕ МОНОДИСПЕРСНОЙ ПЫЛИ В ДВУМЕРНОМ ФАКЕЛЕ
 20 апреля, 2013
20 апреля, 2013  admin
admin Горение угольной пыли в камерной топке протекает в неизотермической запыленной газовой струе, распространяющейся в среде высокотемпературных топочных газов. В зависимости от способа подачи вторичного воздуха запыленная струя распространяется либо непосредственно в топочной среде, либо вместе с окружающим ее потоком вторичного воздуха. В этом параграфе рассматривается более простой случай горения в пылевоздушной струе, распространяющейся в топочном пространстве при отсутствии потока вторичного воздуха, при следующих условиях и предположениях: пылевоздушная струя истекает из щелевой горелки прямоугольного сечения. Поэтому можно считать, что имеется плоскопараллельная струя, и рассматриваемую задачу свести к двумерной. Во избежание осложнения задачи рассмотрением процесса воспламенения и горения летучих в качестве топлива принята пыль АШ. При этом для исключения взаимного влияния частиц различных размеров рассматривается монодисперсная пыль. Температура и скорость пылевых частиц и газа в соответствующих точках струи совпадают. Химическое реагирование существенно не влияет на распределение скоростей и концентраций, и поэтому на факел можно распространить закономерности неизотермической, запыленной турбулентной струи.
Интенсивный конвективный нагрев в турбулентном пограничном слое струи подготавливает пылевоздушную смесь к воспламенению. Во всем пограничном слое струи могут протекать химические реакции, но с разной скоростью в различных ее точках, в зависимости от температуры и концентраций реагирующих веществ, наличия инертной среды и интенсивности теплоотвода. Следовательно, температурные, концентрационные и динамические условия, в которых протекает горение угольной пыли в камерной топке, создаются в турбулентных горелочных струях и определяются интенсивностью массо - и теплообмена в них и характером распространения их в топочных газах. Поэтому физические 360
условия горения в турбулентных струях определяются закономерностями распределения температур, концентраций компенентов реагирующей смеси и полями скоростей.
Вследствие автомодельности течения в пограничном слое турбулентной неизотермической двумерной струи лучи, исходящие из обреза щелевой горелки, являются линиями равных безразмерных температур, концентраций горючего и кислорода и равных относительных скоростей. Поэтому расчет горения монодисперсной пыли в двумерном факеле можно свести к расчету ее вдоль этих лучей с учетом турбулентного тепло - и массообмена в процессе горения между лучами в поперечном направлении к оси струи.
Для математического моделирования горения монодисперсной пыли в двумерном факеле может быть использована принятая в § 16-2 логическая модель горения пылеугольной частицы.
Можно принять, что частицы сферической формы и равномерно распределены в потоке, что в условиях высоких температур, характерных для камерных топочных устройств, горение кокса протекает по внешней поверхности частиц, а горение продуктов неполного окисления— в газовом объеме. Тогда процесс горения монодисперсной пыли в двумерной турбулентной струе вдоль лучей может быть описан следующей системой уравнений.
1. Уравнение теплового баланса горения частиц.
[(£Л^,1 -)- Ягф'г) С^ ~^~~32" а,1^2^
Х|^(Г-Г,)-№}(Г-г,.) - 0,0.9 (Т> - 7Че) - ± 5РкС„ I/ = 0.
(16-22)
В уравнении первым членом выражено количество тепла, выделяющегося при протекании поверхностных реакций (16-4), (16-5) и (16-6); вторым — диффузионная теплопроводность потоками кислорода и углекислоты от поверхности частиц; третьим — конвективный теплообмен между частицами и газовой средой; четвертым — теплообмен излучением между частицей и облучателем; пятым — изменение энтальпии частицы.
Здесь и в дальнейшем в уравнениях (16-23), (16-26), (16-27) и (16-29) использованы обозначения величин, принятые соответственно в уравнениях (16-10), (16-14), (16-13), (16-15) и (16-16).
2. Уравнение теплового баланса газовой среды
Уравнение составлено с использованием дифференциального уравне-
Нения теплообмена в пограничном слое плоской струи, которое в рассматриваемом случае записывается в следующем виде:
2<7 = <?т. (6-23)
В уравнении (16-23):
Е# = ‘Х,”цС^'ц ^“з2~£а1 + “з2~ а2^) 32~ а81^2^ —X
Х4г~0 - ~ л*) —тг— (Т ~ Тг) + 6 £Ц-Х*-- (1 - Гр-Лр) -±— V
^ йз°Рк 4 ' РЛм 4 г' 1 8з°?к ' Усы ^
Х(Т - Тт) + адф (5/У)ф (Г‘г - Т‘л) ^ (16-24)
Второй член уравнения (16-23) представляется выражением
|
А = с ‘»т р |
![]() П дТ, т/ дТ и п д ( Рв дТ Тг 1 /1С ос.
П дТ, т/ дТ и п д ( Рв дТ Тг 1 /1С ос.
В уравнениях (16-24) и (16-25):
Ср — теплоемкость газа, кДж/(кг-К);
Х и у — координаты, направленные по оси струи и перпендикулярно к ней, м;
%т — экспериментальная постоянная;
Ив и и — скорость потока на внутренней границе и в пограничном слое струи, м/с;
Рв и рг — плотность газа на внутренней границе и в пограничном слое струи;
Т — температура газов, К.
В уравнениях (16-24) и (16-25) учтены теплота сгорания окиси углерода в газовом объеме, диффузионная теплопроводность за счет потоков СО и С02, конвективный теплообмен между газом и частицами, лучистый теплообмен между газом и облучателем, турбулентный теплообмен в струе и изменение энтальпии газов.
3. Уравнение выгорания частиц
- тг - йг Ж К2еа*+“■>с*+<16-26>
В уравнении:
СІ8 /
^—изменение диаметра частицы на единице длины луча, м/м;
И — скорость потока.
4. Уравнение изменения концентрации кислорода
Изменение концентрации кислорода можно определить из дифференциального уравнения массообмена в пограничном слое струи:
.= -<£• (16-27)
В уравнении (16-27):
Е9о_ = (««, + аг) С^-^- (1 - Гр - А") (16-288)
•'г гк о у см
|
<7°2 — “ т |
![]() П дС. тг дС и тт д ( ?в дС ри —4-рУ“л--- хори -д— х—
П дС. тг дС и тт д ( ?в дС ри —4-рУ“л--- хори -д— х—
Г ох 1 г ду т «в в ду у р ду
В уравнениях (16-28) и (16-29) и соответственно в уравнении (16-27) учтен расход кислорода на образование СО и С02 в первичных реакциях, на горение СО в объеме, а также перенос его за счет турбулентного массообмена в струе.
В уравнениях
ДС
^------ изменение концентрации кислорода на единице длины лу
Ча, кг/м3;
Ь — ширина пограничного слоя, м.
5. Уравнение изменения концентрации углекислого газа
Изменение концентрации углекислого газа соответственно определяется из дифференциального уравнения переноса в пограничном слое струи:
|
|
В уравнении учтено образование СО2 при первичном реагировании углерода с кислородом при горении СО в объеме, расход СО2 в восстановительной реакции, а также перенос С02 в процессе турбулентного обмена в струе.
Система уравнений (16-22), (16-23), (16-26), (16-27) и (16-29)
Должна быть решена для заданных значений размера и температуры частиц и определяемых расчетом начальных величинах температуры газовой среды и концентраций кислорода и углекислоты в струе на выделенных лучах.
Начальные температуры газовой 'среды на выделенных лучах определяются по заимствованной из [Л. 15] формуле:
|
^'°ОаВ ____ ^^СОгК ^^СОаВ __________ Т°г. К------ ^°Г. В — С°0^СОзН - ^СОзв 1°г-н — т°г. в |
|
А начальные концентрации кислорода и углекислоты определяются на основе подобия температурных и концентрационных полей: |
|
(16-32) |
|
|
 |
![]()
В формулах индексами «к», «н» и «в» соответственно выделены значения начальной концентрации кислорода и углекислоты и температуры на лучах, концентрации этих газов и температуры на наружной и внутренней границах; т] — безразмерная поперечная координата, изменяющаяся от наружной до внутренней границы в пределах от 0 до 1.
14- 5. ГОРЕНИЕ УГОЛЬНОЙ ПЫЛИ В ФАКЕЛЕ
В факеле полидисперсной пыли одновременно происходит горение частиц, которые по размеру отличаются между собой на один-два и даже три порядка. В результате перемешивания в потоке в макрообъемах температура и состав газовой среды выравниваются и в ходе реагирования изменяются, оставаясь одинаковыми для частиц различных фракций. Однако из-за различной интенсивности тепло - и массообмена концентрация газовых реагентов у поверхности частиц различных размеров и их температуры при горении будут существенно отличаться. Это отражается на продолжительности нагрева частиц, па выходе летучих из фракций различных размеров, на режиме и удельной скорости их горения. Кроме того, частицы разных размеров в различной степени охвачены внутренним реагированием.
В процессе нагрева и реагирования частиц летучие, содержащиеся в топливе, выделяются и переходят в газовую среду, пылевые частицы находятся в состоянии конвективного теплообмена с газовой средой, а система — в состоянии теплообмена излучением от реагирующей смеси с окружающей средой газового объема и ограничивающими поверхностями.
В различных исследованиях горения угольной пыли в факеле поли - дисперсность учитывалась в основном двумя методами. Первый метод, примененный В. Гумцем и X. Хоттелем, А. Б. Резняковым, В. В. Померанцевым. С. Л. Шагаловой, К - М. Арефьевым, А. П. Баскаковым и др., основан на введении суммарных характеристик полидисперсности пыли в основные уравнения выгорания топлива.
Вторым методом, применяемым в исследованиях МЭИ, полифракционность учитывается разделением угольной пыли на несколько фракций. В каждой из этих фракций размер частиц усредняется так, чтобы определенная по его величине поверхность равнялась суммарной поверхности пыли рассматриваемой фракции. Затем производится расчет параллельного выгорания частиц различных фракций.
В ряде работ, в которых использовалось распределение угольных частиц по закону Розина — Рамлера, даже при принятых существенно упрощающих допущениях (изотермические условия, протекание реакций в кинетической или диффузионной области, по составу продуктов сгорания), аналитическое решение полученных зависимостей не представлялось возможным или получалось громоздким.
В цкти создана методика расчета выгорания однородного по сечению полифракционного прямоточного факела, которая нашла определенное практическое применение [Л. 52]. Авторы В. В. Померанцев,
С. Л. Шагалова, Б. Д. Кацнельсон и К - М. Арефьев исходили из предположения, что б любой момент времени частицы всех размеров сгорают при одинаковой концентрации кислорода у поверхности при некоторой средней температуре факела в одинаковой области реагирования. Средняя температура факела определялась из уравнения выгорания факела, записанного для кинетической или диффузионной области.
Результаты расчетов приводятся в виде номограмм, по которым можно определить время выгорания полифракционного факела при заданном механическом недожоге или величину недожога при заданном времени сгорания. Авторами показано, что увеличение степени полидисперсности любых твердых топлив приводит к значительному снижению механического недожога.
ВТИ выполнено математическое моделирование воспламенения и первичного выгорания полидисперсной пыли в турбулентных струях.
Далее в настоящей главе использован второй метод — расчет параллельного выгорания частиц различных фракций.

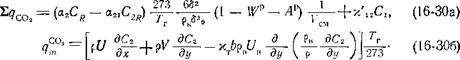
 Опубликовано в
Опубликовано в