После того как состав полупроводника определен, р — п-пе­реход обычно создается путем диффузии цинка в эпитаксиально выращенный материал я-типа [44]. Диффузия примесей в со­единениях AmBv рассмотрена в разд. 5,2, поэтому мы не будем здесь останавливаться на этом вопросе. Обсудим конструктив­ные соображения [45], связанные с квантовым выходом для внутренней поверхности полупроводника, граничащей с неглу­боким р — я-переходом; при этом полупроводник тройного со­става будем предполагать однородным. Влияние переменного состава тройного твердого раствора на коэффициент и способы вывода света через поверхность полупроводникового материала будут рассмотрены в последующих разделах.

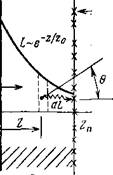
Схема перехода, излучающего свет, представлена на рис. 6.17. Если глубина перехода 1п мала по сравнению с поперечными размерами диода, задача становится одномерной, и именно та­кой она рассматривается в дальнейшем.

Концентрация неосновных носителей, инжектированных в p-область, убывает экспоненциально, за исключением тех носи­телей, которые достигают поверхности и рекомбинируют на центрах безызлучательной рекомбинации. Генерация света в единице объема и концентрация неосновных носителей опреде­ляются уравнением диффузии.

Число квантов, генерируемых в единице объема и в единич­ном энергетическом интервале на расстоянии I от р.— гс-пере - хода, равно

L(E, Z)^-^exp(--~)g(E). (6.34)

Величина Lq — постоянная, а

ZD = (ikBTxfe) (6.35)

где ц — подвижность, е — заряд электрона, т — время жизни неосновных носителей, g(E)—нормированное спектральное рас­пределение излучения, удовлетворяющее условию

оо

5 g(E)dE = 1, о

є>

центры безызлу­чательной реком­бинации

о

п р

Рис. 6.17. Схема излучающего р — я-перехода в прямозонном полупроводнике постоянного состава [45].

а остальные обозначения имеют обычный смысл. Если поверх­ности достигает только свет, излучаемый в направлении Z, и если этот свет поглощается со скоростью а(Е) на единицу

длины, то число квантов, достигших поверхности, будет равно

zn

М£) = $ Р (Е, Z) ехр (- JL) dZ, (6.36)

где Р(Е, Z)—вероятность того, что фотон с энергией Е, излу­ченный на расстоянии Z от начала координат, достигнет поверх­ности. Поскольку Р(Е, Z) описывается интегральной показатель­ной функцией, вычисление LS{E) по формуле (6.36) можно вы­полнить только численными методами.

Можно, однако, записать приближенное выражение для Р(Е, Z) в виде■ • -

. Р (Е, Z)« >/2 exp l-a'(E) (Zn - Z)], (6.37)

где

а'(Е) = 2,2а(Е), (6.38)

т. е. эффективный коэффициент поглощения а' приблизительно вдвое больше коэффициента поглощения материала а. Такое увеличение поглощения обусловлено дополнительными потерями света, который излучается под углами, отличными от нормали к поверхности р — я-перехода.

Подставляя выражение (6.37) в выражение (6.36), можно получить выражение для интенсивности света, достигающего внутренней поверхности, расположенной на расстоянии Z„ от начала координат. В результате поверхностный квантовый вы­ход для р — «-перехода, который определяется как число кван­
тов (достигающих внутренней поверхности p-слоя в точке Z„), отнесенное к проходящему через переход единичному заряду, оказывается равным

п — ті С texp z«a'(g)> ~ ехр (~ Z«/Zp)1 g (F ЗР ҐВШ

Лг® Лв} 2 {1 — ZDa'(E)) g(E)dE, (6.39)

где г)в — квантовый выход в объеме полупроводника. Из выра­жения (6.39) следует, что квантовый выход стремится к нулю при уменьшении глубины р — /г-перехода до нуля. Это очевид­но, поскольку при этом стремится к нулю объем, в котором происходит излучательная рекомбинация, и все проходящие че­рез переход носители выводятся из p-слоя безызлучательно, например путем рекомбинации на поверхности полупроводника. Квантовый выход р — /г-перехода стремится к нулю также и при Z„-v оо, поскольку весь свет поглощается внутри полупровод­ника. Квантовый выход достигает максимума при некоторой глубине р — я-перехода ZnK&кс, определяемой из условия

d4isldZn — 0. (6.40)

Общее решение уравнения (6.40) требует, однако, некоторой априорной гипотезы относительно вида зависимостей спектраль­ного распределения g{E) и эффективного коэффициента погло­щения а' от энергии. Обычно вид этих зависимостей найти не удается; тем не менее для большинства практических систем можно получить разумное приближение, рассматривая частный случай, когда g(E) описывается гауссовым распределением, a a'(E)—степенным рядом, причем для обеих функций отсчет энергии производится от точки Ер, соответствующей максимуму интенсивности генерируемого света. Таким образом,

g (Е) = —exp [- {{Е - Ер)/А}2] (6.41)

Д уп

а' (Е) = Z< (Е - Еру «< + а[{Е - Ер). (6.42)

Решая при этих предположениях уравнение (6.40), можно найти явное решение для некоторых случаев, чаще всего встречаю­щихся на практике. При условии aZp 1 оптимальная глубина перехода Zn макс определяется выражением

+%Ш][-,-^] >"№„]■ (6.43)

Отсюда видно, что конечная ширина линии А и спектральная зависимость коэффициента поглощения а'(Е) приводят к уве-

г, о

/

г, а

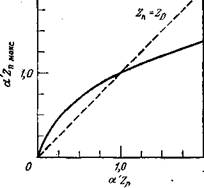
Рис. 6.18. Зависимость оптимальной глубины Zn макс ИЗЛучаЮЩЄГО р — /2-ПЄр6“ хода от диффузионной длины неосновных носителей [45].

личению оптимальной глубины р— я-перехода Z„ макс. Относи­тельное увеличение оптимальной глубины перехода прямо про­порционально произведению Аа' и обратно пропорционально коэффициенту поглощения в максимуме излучения. Причина увеличения оптимальной глубины перехода состоит в том, что конечные значения А и а' всегда сдвигают максимум спектра в область меньшего поглощения и тем самым снижают эффек­тивное значение а. Это приводит к увеличению соответствующей оптимальной глубины р — /г-перехода.

Особенно простым является случай пренебрежимо малой ширины линии (А = 0) или слабой зависимости коэффициента поглощения от энергии (а' да 0). Согласно выражению (6.43), оптимальная глубина перехода при этом определяется выраже­нием

a'Z

п макс

(6.44)

где а'—коэффициент поглощения, соответствующий максимуму излучения (индексы опущены).

Зависимость оптимальной глубины перехода ZnMакС от диф­фузионной длины показана на рис. 6.18. При a ZD < 1 опти­мальная глубина перехода превосходит диффузионную длину. При малом коэффициенте поглощения а' для получения макси­мального числа актов излучательной рекомбинации р — «-пере­ход должен залегать глубоко. При a'ZD > 1 оптимальная глу­бина перехода Zn макс <i Zd в этом случае сильное внутреннее поглощение требует мелкого залегания перехода. На практике величина a'Zo редко превышает 2; например, в GaAs макси-

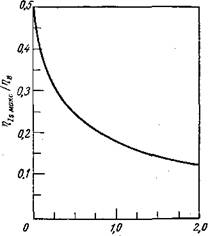
Рис. 6.19. Зависимость отношения максимального квантового выхода г)« макс на примыкающей к переходу внутренней поверхности прямозонного полупро­водника к полному квантовому выходу в объеме полупроводника rjs (т. е. доли света, достигающей поверхности) от произведения эффективного коэф­фициента поглощения на диффузионную длину неосновных носителей ol'Zd [45].

мальный коэффициент поглощения а' == 104 см-1, а диффузион­ная длина Zd = 2 мкм, так что a'ZD = 2.

Максимальный квантовый выход на внутренней поверхности перехода r]/s макс, соответствующий оптимальной глубине пере­хода, можно найти, подставляя выражение (6.44) в выражение

(6.39) и пренебрегая влиянием ширины спектрального распре­деления. В результате получим

Л/.максЛів = 7а (a'ZD)51%-. (6-45)

где т]в — объемный квантовый выход, введенный в выражение

(6.39) . Зависимость отношения ri/s макс/Лв от a'ZD приведена на рис. 6.19. Наилучший вывод света получается при малых ol'Zd, т. е. когда глубокое залегание перехода сочетается с малым ко­эффициентом поглощения (как в GaP). В однородном прямо­зонном полупроводнике, например в диффузионном диоде из GaAs, величина a'ZD приближается к 2, так что доля излучае­мого внутри света, которая достигает внутренней поверхности полупроводника в случае рекомбинации свободных носителей, падает до 12%. Оптимальная глубина перехода для такого при­бора обычно составляет Zn макс « 0,7 ZD-

Эмпирическое определение величины a'ZD во многих слуяаях является наиболее прямым и правильным подходом. При этом

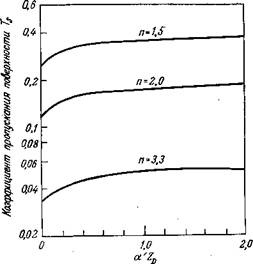
Рис. 6.20. Зависимость коэффициента пропускания поверхности Т* от a'Zn для однородного прямозонного полупроводника (п = ПііПе) [45].

определяется спектр излучения и квантовый выход слоя при фотолюминесцентном возбуждении. Коэффициент поглощения a(hv) берется из опубликованных данных или определяется экспериментально. Аналогично, измеряя квантовый выход и время затухания, можно найти диффузионную длину. Таким об­разом, можно вычислить a'ZD и определить оптимальную глу­бину перехода либо по формуле (6.44), либо по рис. 6.18. Точно так же квантовый выход электролюминесценции можно пред­сказать либо по формуле (6.45), либо по рис. 6.19.