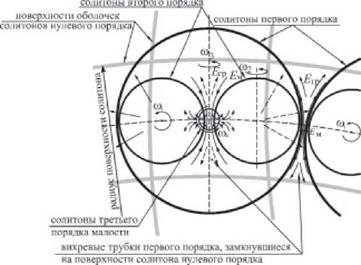
На рис. 3, с. 73, показана система разномасштабных элементарных структур энергии, состоящая из четырёх последовательно возникающих во фрактале разно­масштабных геометрических структур, но взаимосвязанных и условно совмещён­ных в одной «картинке». Структуры находятся в сложных иррациональных взаи­мосвязях. Сложность и разномасштабность взаимосвязанных солитонов является причиной того, что их движение во фрактале возможно только как последователь­ное движение-вращение энергии в одностороннем пространстве и благодаря его свойствам. Вращения каждой пары солитонов и взаимосвязанных с ними вихрей должны быть в целом и взаимно-ортогональными. Эго является причиной трёх­мерности фрактала и, следовательно, трёхмерности пространства, но в достаточно «большом», поскольку материя и её свойства обусловлены явным проявлением только сконденсированной составляющей энергии.

Последовательность движения разномасштабных структур неразличима по той причине, что инерция и сжимаемость сконденсированной энергии «искажает детерминизм» движения несконденсированной энергии.

Фрактал, наблюдаемый в ограниченном диапазоне геометрических масшта­бов, может находиться в динамическом равновесии, как волновое движение энер­гии, сохраняя и воспроизводя свою геометрическую структуру лишь при условии последовательного совершения на всех ап только по одному обороту, периодически («волнообразно») заменяясь себе подобной системой «очередного масштаба». Эго про­исходит благодаря преобладанию тока через фрактал несконденсированной энергии из бесконечно малых геометрических масштабов в - бесконечно большие... над стоком. Всего один оборот частицы при её движении в оболочках солитонов и вихревых трубок всех масштабов - это необходимое условие существования квантового ва­куума в виде фракталов энергии и неразрывного движения идеальной жидкости, в динамике - турбулентного.

В каждой точке, нарисованной на рис. 3 «картинки», сконденсированная энер­гия имеет различное и ненулевое значение плотности. Поскольку все точки взаи­мосвязаны и находятся в криволинейном движении, то на все точки действуют разные по величине движущие неуравновешенные силы - центробежные и цен­тростремительные (по Тимофееву), создающие непрерывные изменения всей гео­метрии «картинки».

При затрубленном анализе движения гипотетической точки-кванта несконден - сированной энергии переход от одного целочисленного значения масштаба к дру­гому (от одной оболочки к другой оболочке) происходит дискретно, но в антропо­морфном восприятии, т. к. перенос энергии через вихревые трубки, заполняющие межсолитонные пространства, идёт «слишком быстро». Поэтому внутри каждого масштаба (внутри оболочки) каждая точка-вектор, принадлежащая оболочке, со­вершает в ней всего один оборот, в конце которого возникает «быстрый процесс скачка» в другую оболочку следующего масштаба.

Возникает парадокс: кванты сконденсированной энергии, даже гипотетиче­ские, методически не могут переходить из одной оболочки в другую, следующую по масштабу, т. к. у них разная плотность энергии. Парадокс разрешается тем, что это происходит вследствие «быстрой конденсации» (накачки) в этот квант нескон - денсированной энергии в процессе перехода через вихревое состояние в межоболо­чечном пространстве. Но в новую оболочку попадает уже другой квант.

«Всего один оборот» в оболочке, независимо от размеров солитона, т. е. пре­образование двух видов энергии с разной частотой в разных масштабах - это не­обходимое условие существования фрактала как системы разнородных солитонов, связанных в одну волновую структуру энергии, протяжённую в пространстве и времени существования. Это одно из условий реализации детерминизма в турбу­лентном движении энергии в квантовом вакууме.

«Всего один оборот» - это методическое решение, принятое для достаточно грубых геометрических масштабов. Это позволяет на основании предложенной аксиоматической системы квантового вакуума игнорировать тот факт, что при сопряжении кривых с разными радиусами кривизны математические модели кри­вых в точке сопряжения терпят разрыв. Оно порождает другие методические про­блемы, которые могут изменяться качественно, но не исчезают ни при каких об­стоятельствах и которые разрешаются также методически по мере возникновения. Рассмотрим ряд следующих примеров.

Точка сопряжения имеет геометрическую структуру, сложность которой зави­сит только от выбора геометрического масштаба её анализа. В грубом масштабе - это число и потенциал энергии. В менее грубых масштабах - это узловая точка гар­монической кривой, полюс солитона, отображающие динамически равновесный процесс преобразования двух видов энергии. В достаточно малом масштабе (при соответствующем возрастании частоты преобразований) - это экспонента, харак­теризующая лавинный процесс конденсации. В ещё меньшем масштабе - это снова точка, принадлежащая названной экспоненте. При дальнейшем неограниченном уменьшении масштабов предложенная схема повторяется по закону чисел Фибо­наччи для несконденсированной составляющей энергии и по закону простых чисел для сконденсированной.

Строго говоря, гармоническая кривая - это «плоская геометрическая модель» динамически равновесного состояния энергии с переменным радиусом в каждой точке кривой. Эго означает: сконденсированная энергия должна ветвиться в каж­дой точке синусоиды, мощность ветвления в которых различна, что объясняет

ветвления-излучения энергии. Есть, по меньшей мере, ещё несколько вариантов объяснений излучения энергии каждой точкой-солитоном как вихрем и суще­ственно особой точкой, которые зависят от рассматриваемого геометрического масштаба. Область ветвления «чувствительна» к выбору геометрического масшта­ба анализа, но наибольшая мощность ветвления наблюдается только на низших амплитудах, т. е. в узловых точках синусоиды в области её пересечения с осью абсцисс, где радиус кривизны наибольший.

При сопряжении кривых с различными радиусами кривизны «точки-области» сопряжения апроксимируются в достаточно малых масштабах также кривыми с переменными радиусами кривизны.

По физическому содержанию они рассматриваются как области ортогональ­ного ветвления токов несконденсированной энергии, а по математическому - раз­ложения в ряды и числовые последовательности - одномерные модели токов энер­гии.

При поиске геометрических моделей областей ветвления, в связи с их много­вариантностью, использована идея Клейна о возможности взаимных преобразова­ний разнородных геометрий.

Для решения методических проблем, связанных с перечисленными, в анализ квантового вакуума введены свойства односторонних и двусторонних пространств и взаимно внешних координатных систем, которые рассмотрим в главе 5.