Геометрические инструкции
 8 января, 2013
8 января, 2013  admin
admin Геометрическими называются инструкции для определения геометрических элементов, используемых при описании траектории инструмента. Это наиболее обширная группа инструкций СПД ЧПУ, да и вообще всех систем автоматического программирования, поэтому их описанию необходимо уделить особое внимание.
Геометрическими элементами явля ются точки, прямые, окружности, кривые второго порядка и т. д. Идентификаторы геометрических переменных могут быть простыми или индексированными. Язык СПД ЧПУ не зависит от выбранной единицы длины. Однако для удобства линейные размеры задают в миллиметрах, углы — в градусах (десятичным числом). Угол считается положительным, если его отсчет рассматривается против часовой стрелки от положительного направления - оси абсцисс (X). Все геометрические элементы программы задаются пользователем (программистом) в удобной для него системе координат, которая выбирается без какой-либо привязки к конкретному станку.
Прямые и окружности определяются в плоскости XOY. Для всех точек, если значение координат по оси Z не указывается, оно принимается равным нулю.
Геометрические инструкции начинаются главным словом, за которым стоит символ /. Второстепенная часть позволяет уточнить определение элемента, заданного главным словом. Общий вид геометрической инструкции:
Л=В/С,
Где А — идентификатор геометрической переменной (простой или индексированной); В — главное слово; С — второстепенная часть, уточняющая геометрический элемент.
Инструкции определения точек. Геометрические инструкции, определяемые главным словом POINT, позволяют найти точку одним из приведенных ниже способов.
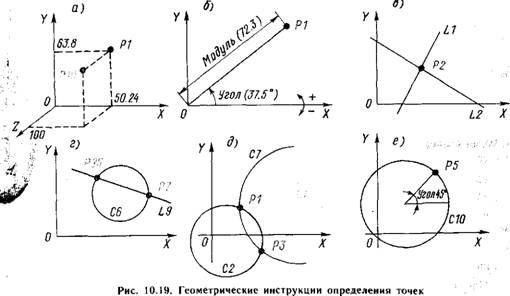
1. Точка, определяемая прямоугольными координатами. На рис. 10.19, а показан пример определения точки по заданным координатам х, у, г. За главным словом POINT во второстепенной части инструкции не следуют никакие вспомогательные слова, уточняющие данную точку:
T04KA=P0INT/X, Y,[Z]
Pl=PC>iNT/50. 24,63. 8
P10=POINT/50.24,63.8,100
2. Точка, определяемая полярными координатами (рис. 10.19, б):
Вспомогательные слова RTHETA и XYPLAN указывают на то, что точка определяется полярными координатами в плоскости XOY. Параметр МОДУЛЬ указывает на модуль вектора, соединяющего точку с началом координат, а параметр УГОЛ — на угол между вектором и осью X.
3. Точка, определяемая пересечением двух прямых (рис. 10.19, в):
T04KA=P0INT/INT0F,ПРЯМАЯ1,ПРЯМАЯ2
P2=POINT/INTOF, LI,L2
Вспомогательное слово INTOF указывает, что точка определяется пересечением. Параметры ПРЯМАЯ1 и ПРЯМАЯ2 — идентификаторы двух предварительно найденных пересекающихся прямых.
|
T04KA=P0INT/RTHETA,XYPLAN,МОДУЛЬ, УГОЛ Pl=POINT/RTHETA, XYPLANE,72.3,37.5 |
4. Точка, определяемая пересечением прямой с окружностью (рис. 10.19, г):
Идентификаторами ПРЯМАЯ и ОКРУЖНОСТЬ задаются предварительно установленные пересекающиеся прямая и окружность. Модификаторы XSMALL, XLARGE, YSMALL, YLARGE позволяют однозначно указать одну точку пересечения прямой с окружностью. На выбор точки пересечения с меньшим значением координаты х указывает модификатор XSMALL, с меньшим значением У — модификатор YSMALL. Модификаторы XLARGE и YLARGE означают, что надо выбрать большее значение координат X и Y соответственно. Согласно рис. 10.19, г, точки Р7 и Р25 можно определить следующим образом:
P7=PGINT/YSMALL, INTOF, L9,С6
Р2 5 =POINT/YLARGE,INTOF, L9,С6
Частные случаи: для горизонтальных прямых применяют только модификаторы XSMALL и XLARGE, для вертикальных — только YSMALL и YLARGE.
5. Точка, определяемая пересечением двух окружностей (рис. 10.19, д):
|
XSMALL XLARGE YSMALL YLARGE |
|
T04KA=P0INTI |
INTOF, v. ПРЯМАЯ, ОКРУЖНОСТЬ, INTOF, ОКРУЖНОСТЫ,
|
XSMALL XLARGE YSMALL YLARGE |
|
T04KA=P0INT / < |
Окружностьг
Ч
Идентификаторы ОКРУЖНОСТЬ! и ОКРУЖНОСТЬ2 задают две предварительно найденные окружности. Модификаторы XSMALL, XLARGE, YSMALL и YLARGE позволяют однозначно указать точку пересечения двух окружностей. Эти модификаторы используются так же, как и при определении точки пересечения прямой с окружностью. Точки РЗ и Р1, показанные на рис. 10.19, д, можно найти следующим образом:
P3=POINT/YSMALL,INTOF,С7,С9
Pl=POINT/YLARGE, INTOF,С7,С9
6. Точка на окружности, определяемая центральным углом (рис. 10.21, е):
ТОЧКА=РОШТ/ОКРУЖНОСТЬ, ATANGL, УГОЛ
P5=POINT/dO,ATANGL,4 5
Идентификатор ОКРУЖНОСТЬ задает предварительно определенную окружность. Вспомогательное слово ATANGL указывает на то, что точка задается углом. Идентификатор УГОЛ задает значение угла между радиусом окружности, соединяющим центр с определяемой точкой, и осью X.
Инструкции определения прямых. Задаются главным словом LINE и второстепенной частью и находят прямую одним из указанных ниже способов. Предполагается, что прямая расположена в плоскости XOY, если не введены дополнительные инструкции преобразования координат (они рассмотрены ниже).
1. Прямая, проходящая через две точки (рис. 10.20, а):
NPHMAH=LINE/T04KAl,ТОЧКА2
NPHMAH=LINE/Xl,Y1,Х2,Y2
Точки, необходимые для определения прямой, могут задаваться идентификаторами ранее найденных точек или значениями их координат. Идентификаторы ТОЧКА1 и ТОЧКА2 задают две предварительно определенные точки, идентификаторы XI, У1, Х2 и У2 — координаты точек:
L1=LINE/P7,P9
Ll=LINE/60,47.8, 25, 55
Для примера определим прямые, пересекающие оси X и У:
LX=LINE/0,0,30,0
LY=LINE/0,0,0, 30
Прямая LX проходит через точки с координатами 0,0 и 30,0, т. е. через точки, лежащие на оси X. Прямая LY проходит через точки, лежащие на оси У.
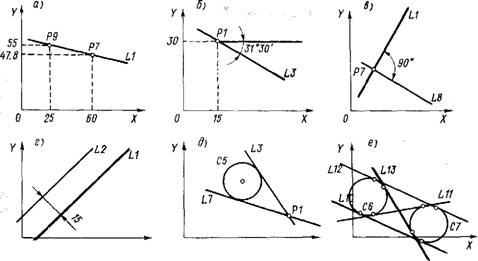
2. Прямая, проходящая через точку под заданным углом к оси X (рис. 10.20, б)
IlPflMAfl=LINE/ТОЧКА, ATANGL, УГОЛ
|
X 0 X 0 Рис. 10.20. Геометрические инструкции определения прямых |
Идентификатор ТОЧКА задает предварительно найденную точку, идентифи
катор УГОЛ — значение угла между определяемой прямой и осью X. Вспомогательное слово ATANGL указывает на то, что определяемая прямая будет задаваться углом:
L3=LINE/P1,ATANGL,-31.5
L3=LINE/15,30,ATANGL,-31.5
3. Прямая, проходящая через точку, перпендикулярная к заданной прямой (рис. 10.20, в):
ПРЯМАЯ=LINE/ТОЧКА, PERPTO, ПРЯМАЯ
L1=LINE/P7,PERPTO, L8
Идентификаторы ТОЧКА и ПРЯМАЯ задают предварительно найденные точку и прямую, вспомогательное слово PERPTO указывает, что определяемая прямая перпендикулярна к заданной.
4. Прямая, параллельная заданной прямой на заданном расстоянии (рис. 10.20, г):
NPHMAH=LXNE/PARLEL, ПРЯМАЯ1г
РАССТОЯНИЕ
Идентификаторы: ПРЯМАЯ 1 — задание предварительно найденной прямой; РАССТОЯНИЕ — указание расстояния в плоскости XOY от ПРЯМОЙ 1 до опре - ляемой прямой. Модификаторы XSMALL, YSMALL, XLARGE и YLARGE позволяют однозначно указать положение искомой прямой относительно ранее определенной. ПРЯМУЮ 1 можно определить и так (рис. 10.20, г):
LI=LINE/PARLEL, L2,YSMALL,15
Если ПРЯМАЯ 1 параллельна оси X, используются модификаторы YSMALL и YLARGE; если ПРЯМАЯ1 параллельна оси Y — модификаторы XSMALL, XLARGE. Вспомогательное слово PARLEL указывает, что определяемая прямая параллельна заданной.
5. Прямая, проходящая через точку и касающаяся окружности (рис. 10.20, д):
FRight]
NPHMAH=LINE/T04KA,-s „„ > ,TANTO, I LEFT j
ОКРУЖНОСТЬ
Идентификаторы ТОЧКА и ОКРУЖНОСТЬ задают предварительно определенные точку и окружность, модификатор RIGHT уточняет, что точка касания находится справа от прямой, соединяющей заданную точку с центром окружности (если смотреть из заданной точки в направлении центра окружности). Модификатор LEFT уточняет левое расположение точки касания. Вспомогательное слово TANTO указывает на касание геометрических элементов:
L7=LINE/P1,LEFT, TANTO, С5
L3=LINE/P1,RIGHT, TANTO, С5
6. Прямая, касающаяся двух окружностей (рис. 10.20, е):
[right]
,TANTO,
NPHMAH=LINE
[LEFT J ГRIGHT]
Окружносты ,__ у, tanto,
ОКРУЖНОСТБ2
Идентификаторы ОКРУЖНОСТЫ и ОКРУЖНОСТЬ2 задают две предварительно определенные окружности, модификаторы RIGHT и LEFT указывают положение точки касания относительно прямой, соединяющей центры окружностей, если смотреть из центра первой окружности в направлении центра второй окружности. Показанные на рис. 10.20, е прямые L10, LI 1, L12 и L13 можно определить следующим образом:
L10=LINE/LEFT, TANTO, С7,LEFT, TANTO, С6 LI1=LINE/RIGHT, TANTO, C7, LEFT, TANTO, C6 L12=LINE/RIGHT, TANTO, C7,RIGHT, TANTO, C6
LI3=LINE/LEFT, TANTO, C7.RIGHT, TANTO, C6
Инструкции определения окружностей. Геометрические инструкции с главным словом CIRCLE позволяют определить окружность одним из перечисленных ниже способов. При этом, как уже говорилось, размеры по оси Z не учитываются, т. е. предполагается, что окружность расположена в плоскости XOY.
1. Окружность, определяемая центром и радиусом (рис. 10.21, а):
ФОРМАТ 1: OKPJTfCHOCTb=CIRCLE/X, Y,
РАДИУС
Е>
|
|
|
Ct |
|
С7. |
|
PJ |
Рис. 10.21. Геометрические инструкции определения окружностей
ФОРМАТ 2: OKpy5KHOCTb=CIRCLE/CENTER, ТОЧКА,RADIOS,РАДИУС
В ФОРМАТЕ 1: X и Y — координаты центра окружности; РАДИУС — значение радиуса окружности или идентификатор скалярной переменной, равной радиусу окружности. В ФОРМАТЕ 2: идентификатор ТОЧКА задает предварительно найденную точку, которая будет служить центром окружности; вспомогательное слово CENTER указывает, что окружность определяется через координаты центра; слово RADIUS означает радиус окружности.
2. Окружность, определяемая радиусом и касающаяся двух пересекающихся прямых (рис. 10.21, б):
OKPyaCHOCTb=CIRCLE К
-,ПРЯМАЯ,RADIOS,РАДИУС
Прямые, которых касаются окружности, предварительно известны; РАДИУС — значение радиуса. Модификаторы XSMALL, XLARGE, YSMALL и YLARGE задают позицию центра определяемой окружности относительно пересекающихся прямых (выше прямой, ниже, слева, справа). Окружности на рис. 10.21, б можно описать следующим образом:
C1=CIRCLE/XLARGE,L7,YSMALL,L9,
RADIOS,15
C2=CIRCLE/XSMALL,L7,YSMALL,L9,
RADIOS,15
C3=CIRCLE/XSMALL,L7,YLARGE,L9,
RADIUS,15
C4^CIRCLE/XLARGE, L7,YLARGE, L9,
RADIOS,15
Окружности можно задать и другими модификаторами при условии, что они однозначно определят требуемую окружность. Например, окружность С4, как и все остальные (см. рис. 10.21, б), можно задать так:
C4=CIRCLE/YSMALL,L7,XLARGE,L9,
RADIUS,10
|
,ТОЧКА, > RADIUS, РАДИУС |
|
ПРЯМАЯ "S |
3. Окружность, определяемая радиусом, касающаяся прямой и проходящая через точку (рис. 10.21, в):
OKP5TRHOCTb=CIRCLE/TANTO, XSMALL XLARGE YSMALL YLARGE
ПРЯМАЯ и ТОЧКА — предварительно найденные прямая и точка. Точка может принадлежать или не принадлежать заданной прямой. РАДИУС — значение радиуса определяемой окружности. Модификаторы XSMALL и YSMALL уточняют позицию центра радиуса определяемой окружности относительно заданной точки. На основании рис. 10.21, в:
С8 ^CIRCLE/TANTO,LI,XLARGE,Р6, RADIUS,25
C7=CIRCLE/TANTO, LI,XSMALL,P6, RADIOS,25
Вместо модификатора XLARGE можно поставить модификатор YSMALL, но это не нарушает однозначности определения окружностей С8 и С7.
4. Окружность, определяемая радиусом, касающаяся прямой и дуги окружности (рис. 10.21, г):
OKPWKHOCTb=CIRCLE / -Ч
XSMALL
XLARGE I J IN
YSMALL Г ' 1 OOT
YLARGE
С1=CIRCLE/YLARGE,L20,XSMALL,OOT,C9, RADIOS,15
C4=CIRCLE/YSMALL, L20,YLARGE, IS, C9, RADIUS,15
Идентификаторы ПРЯМАЯ и ОКРУЖНОСТЬ — предварительно найденные прямая и окружность. РАДИУС — значение радиуса определяемой окружности. Модификаторы IN и OUT указывают, что центры двух окружностей находятся по одну или по разные стороны от точки касания (IN — внутреннее касание, OUT — внешнее касание). Первая группа модификаторов XSMALL, XLARGE, YSMALL, YLARGE — уточняет позицию центра определяемой окружности относительной заданной прямой, вторая группа аналогичных модификаторов уточняет выбор одной из двух возможных окружностей в зависимости от положения центра. Так, для окружности С1 модификатор YLARGE показывает, что центр окружности расположен выше прямой L20; модификатор XSMALL определяет левое положение С1 относительно окружности С9 и вне ее (OUT).
5. Окружность, определяемая радиусом и касающаяся двух окружностей (рис. 10.21, д):
OKPyraOCTb=CIRCLE,
Г окружностьг,
OKPy*HOCTbl,J I, RADIUS, 1 OUT Г
L J РАДИУС C3=CIRCLE/YSMALL, IN, CI, OUT, C2, RADIUS,21
Идентификаторы ОКРУЖНОСТЬ 1 и ОКРУЖНОСТЬ 2 — две предварительно найденные окружности. Модификаторы IN и OUT указывают на внешнее и внутреннее касание определяемой окружности с каждой из заданных. Модификаторы XSMALL, XLARGE, YSMALL, YLARGE уточняют выбор определяемой окружности в зависимости от положения центра. Так, центр окружности СЗ расположен ниже центра окружности С1, внутри ее (IN); внешнее касание (OUT) с окружностью С2.
6. Окружность, определяемая центром и касающаяся другой окружности (рис. 10.21, е):
ОКРУЖНОСТЬ:: CIRCLE/CENTER, ТОЧКА,
ГLarge!
•< >■ , TANTO, ОКРУЖНОСТЬ
JSMALLj
C1=CIRCLE/CENTER,РЗ,SMALL, TANTO, C7
C2=CIRCLE/CENTER, P3,LARGE, TANTO,С7
Идентификатор ТОЧКА задает предварительно найденную точку, которая будет являться центром определяемой окружности. Идентификатор ОКРУЖНОСТЬ задает предварительно полученную окружность, которой будет касаться определяемая окружность. CENTER и TANTO — вспомогательные слова, указывающие подтип данной инструкции. Модификаторы LARGE и SMALL уточняют выбор одной из двух возможных окружностей (соответственно большую или меньшую).
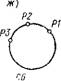
7. Окружность, проходящая через три точки (рис. 10.21, ж):
0KP3TKH0CTb=CIRCLE/T04KA 1, ТОЧКА 2,
ТОЧКА 3
C6=CIRCLE/P3,P2,P1
Три точки однозначно определяют окружность, т. е. координаты центра и радиус. Идентификаторы ТОЧКА 1, ТОЧКА 2, ТОЧКА 3 задают предварительно полученные точки, через которые проходит определяемая окружность.
Инструкция определения контура. Основной формат инструкции КОНТУР =C0NTUR/T04KA 1, ЭЛЕМЕН'1 Ы КОНТУРА И МОДИФИКАТОРЫ, ТОЧКА 2.
КОНТУР — идентификатор определяемого контура.
CONTUR — главное слово, указывающее тип инструкции.
Элементы контура — прямые и окружности, записанные в порядке, соответствующем порядку движения инструмента.
К модификаторам в данной инструкции относятся служебные слова, которые указывают на однозначность движения по элементам контура: CLW — движение по окружности по часовой стрелке; CCLW — движение по окружности против часовой стрелки. Модификаторы XSMALL, XLARGE, YSMALL и YLARGE уточняют точки пересечения прямой и окружности или точку пересечения окружностей, до которой необходимо. двигаться в определенном месте контура.
ТОЧКА 1 и ТОЧКА 2 — идентификаторы точек начала и конца контура. Если точки начала и конца контура совпадают, контур замкнутый, если не совпадают — контур разомкнутый.
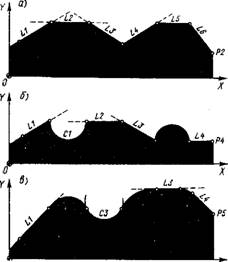
На рис. 10.22 показаны варианты разомкнутых контуров.
Контур, состоящий из одних прямых (рис. 10.22, а):
CONT1=CONTUR/P1,LI,L2,L3,L4,L5,L6,Р2
Вследствие однозначности пересечения здесь отсутствуют модификаторы XSMALL, ..., YLARGE.
Контур с взаимно пересекающимися прямыми и окружностями (рис. 10.22, б):
CONT2=CONTUR/P3,LI,CCLW,YSMALL,CI,
XLARGE,L2,L3,CLW,YLARGE,C2,XLARGE,
L4,P4
В данном случае при описании контура используют модификаторы CLW (по часовой) и CCLW (против часовой стрелки), указывающие направление движения по окружностям, и модифика-
|
О X Рис. 10.22. Примеры разомкнутых контуров |
Торы XSMALL, ..., YLARGE, указывающие точки пересечения элементов.
Контур из элементов, которые касаются друг друга (рис. 10.22, в):
CONT3=CONTUR/P4,LI,CLW,С2,CCLW,СЗ, CLW, C4,L3,CLW, C5,L4,P5
В инструкции описания этого контура использованы только модификаторы CLW и CCLW.
Контур, состоящий из взаимно касающихся друг друга элементов, называют плавным. На практике этот контур встречается чаще других, что обусловлено особенностями ввода коррекций на радиус фрезы в системах с ЧПУ, где необходим плавный сопряженный контур. Но это не исключает возможности использования в СПД ЧПУ и других типов контуров.

 Опубликовано в
Опубликовано в