The simplest form of optical cavity consists of two coplanar mirrors separated by a distance Lcav. About one century ago, Fabry and Perot (1899) were the first to build and analyze optical cavities with coplanar reflectors. These cavities had a large separation between the two reflectors, i. e. Lcav >> X. However, if the distance between the two reflectors is of the order of the wavelength of light, new physical phenomena occur, including the enhancement of the optical emission from an active material inside the cavity. Very small cavities, with typical dimensions of Lcav « X, will be denoted as microcavities.

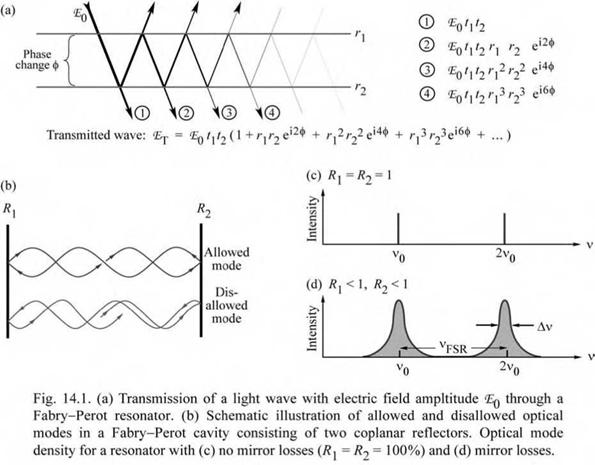
Coplanar microcavities are the simplest form of optical microcavities and their properties are summarized below. For a detailed discussion of the optical properties of Fabry-Perot cavities, the reader is referred to the literature (Coldren and Corzine, 1995; Saleh and Teich, 1991). Fabry-Perot cavities with two reflectors of reflectivity R1 and R2 are shown in Figs. 14.1 (a) and

(b) . Plane waves propagating inside the cavity can interfere constructively and destructively resulting in stable (allowed) optical modes and attenuated (disallowed) optical modes, respectively. (Note that the photon length is much longer than the microcavity length.) For lossless (non-absorbing) reflectors, the transmittance through the two reflectors is given by T1 = 1 - R1 and T2 = 1 - R2. Taking into account multiple reflections inside the cavity, the transmittance through a Fabry-Perot cavity can be expressed in terms of a geometric series. The transmitted light intensity (transmittance) is then given by

condition of constructive interference is fulfilled, i. e. if 2ф = 0, 2n, ... . Insertion of these values into Eq. (14.1) yields the transmittance maxima as

T1 T2

(1 - JiRRf

For asymmetric cavities (R1 ^ R2), Tmax < 1. For symmetric cavities (R1 = R2), the transmittance maxima are unity, Tmax = 1.

Exercise: Transmission through a Fabry-Perot cavity. Derive Eq. (14.1) by calculating the transmitted wave intensity in terms of a geometric series as illustrated in Fig. 14.1 (a).

Near ф = 0, 2n, 4n..., the cosine term in Eq. (14.1) can be expanded into a power series (cos 2ф « 1 - 2ф2). One obtains

T = ----------------------- Т22Т2-------------------- . (14.3)

(l - Jrr )2 + - ДЖ4 Ф2

Equation (14.3) indicates that near the maxima, the transmittance can be approximated by a lorentzian function. The transmittance T in Eq. (14.3) has a maximum at ф = 0. The transmittance decreases to half of the maximum value at ф1/2 = [1 - (R1 R2)12 ] / [4 (R1 R2)12 ]12. For high values of R1 and R2, i. e. R1 « 1 and R2 « 1, it is ф1/2 = (1/2) [1 - (R1 R2)12 ].

The cavity finesse, F, is defined as the ratio of the transmittance peak separation to the transmittance full-width at half-maximum, i. e.

F = peak separation = п = п ^RyRi (144)

peak width 2ф1/2 1 - ■^R1R2 1 - yjR1R2

Inspection of Eq. (14.4) shows that the finesse becomes very large for high values of R1 and R2.

The wavelength and frequency of light are practically more accessible than the phase. Equations (14.1)-(14.4) can be converted to wavelength and frequency using

ф = 2п - nLca^ = 2п nLcav V (14.5)

X c

where Lcav is the length of the cavity, X is the wavelength of light in vacuum, v is the frequency of light, and n is the refractive index inside the cavity. Figures 14.1 (c) and (d) show the transmittance through a cavity with R = 1 and R < 1, respectively. In the frequency domain, the transmittance peak separation is called the free spectral range vFSR, as shown in Fig. 14.1 (d). The finesse of the cavity in the frequency domain is then given by F = vFSR / Av.

Frequently the cavity quality factor Q rather than the finesse is used. The cavity Q is defined as the ratio of the transmittance peak frequency to the peak width. Using this definition and Eq. (14.4), one obtains

q = peak frequency = 2 n Lcav п 4R1 R2 2 n Lcav п

peak width X 1 - ^R1R2 X 1 - JR1R

where the peak width is measured in units of frequency.

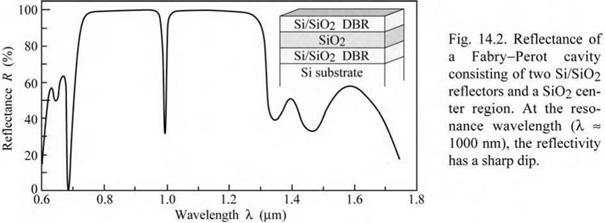
Figure 14.2 shows an example of a reflectance spectrum of a microcavity consisting of a four-pair Si / SiO2 distributed Bragg reflector (DBR) deposited on a Si substrate, a SiO2 center

region, a 2.5-pair Si / SiO2 DBR top reflector. The resonance wavelength of the cavity is approximately 1.0 |j, m. The reflectance of the cavity does not approach zero at the resonance wavelength due to the unequalness of the reflectivities of the two reflectors.