Evaluation of the Double Ellipsoid Model
 17 марта, 2014
17 марта, 2014  admin
admin In order to minimize the computing cost the initial analysis was done in the plane normal to the welding direction as shown in figures 2-19 and 2-20. Thus, heat flow in the welding direction was neglected. The above simplification is accurate in situations where comparatively little heat flows from the arc in the welding direction. This is reasonable when the arc speed is high. An estimate of the effect of this approximation has been given by Andersson [41] who argues that the errors introduced by neglecting heat flow in the direction of the moving electrode are not large, except in the immediate vicinity of the electrode.
|
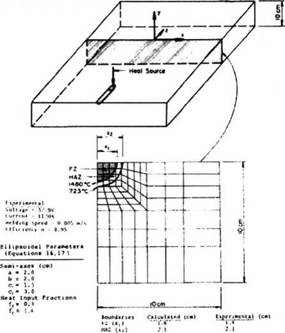
Figure 2-19: Experimental arrangement and FEM mesh for the thick section bead on plate weld [48 and 46]. |
In order to demonstrate the flexibility and assess the validity of the double ellipsoidal heat source model two quite different welding situations were considered.
The first case analyzed was a thick section (10cm) submerged arc bead-on-plate (low carbon structural steel) weld shown schematically in Figure 2-19. The welding conditions are also contained in the Figure.
Christensen [48] reported a 800 to 500 °С cooling time of 37 seconds for this weld and the FZ and HAZ sizes shown in the diagram. Shown also in the figure is the FEM mesh used to calculate these quantities. It is two-dimensional in x and у as previously explained. The temperature distribution in the ‘cross-section analyzed’ is calculated for a series of time steps as the heat source passes. In this way the FZ and HAZ cross-sectional sizes can be determined, and from the time step-temperature data the cooling time 800 to 500 °С is calculated.
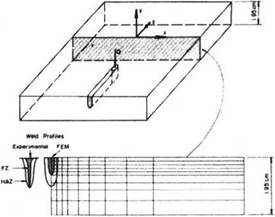
The second welding situation is taken from the work of Chong [49], Figure 2-20.
|
|
Figure 2-20: Experimental arrangement and FEM mesh for the deep penetration weld [46 and 49].
It is a partial penetration electron beam bead-on-plate (low carbon steel) weld. Traditionally the Rosenthal 2D model would be used to analyze this weld. However, there is some heat flow through the thickness dimension since the penetration is partial and, of course, the idealized line heat source is suspect. The ellipsoidal model can be easily adapted to this weld geometry by selecting appropriate characteristic ellipsoidal parameters. A cooling time (800 °С to 500 °С) of 1.9 seconds was measured by Chong [49] and the FZ and HAZ dimensions were reported [46].
In previous works the thermal properties and boundary conditions were usually set equal to a constant value. Convection and radiation are mostly ignored. The point, line and plane sources [37, 38 and 39] idealize a heat source which in reality is distributed. These solutions are most accurate far from the heat source. At the source, the error in temperature is large, usually infinite. Near the heat source the accuracy can be improved by matching the theoretical solution to experimental data. This is usually done by choosing a fictitious thermal conductivity value.
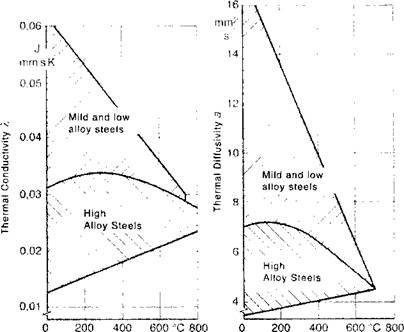
With numerical methods, these deficiencies have been corrected and more realistic models that are just as rigorous mathematically have been developed. Perhaps the most important factor is to distribute the heat rather than assume point or line sources. Temperature dependent thermal conductivity and heat capacity can be taken into account, Figures 2-21 and 2-22. In addition, temperature dependent convection and radiation coefficients can be applied to the boundaries. For the radiation and convection boundary conditions, a combined heat transfer coefficient was calculated from the relationship:
H = 24.1хКГ4£Г161 (2-18)
where є is the emissivity or degree of blackness of the surface of the body. A value of 0.9 was assumed for e, as recommended for hot rolled steel [37].
Contact thermal resistance between the plate and the jigging can be incorporated.
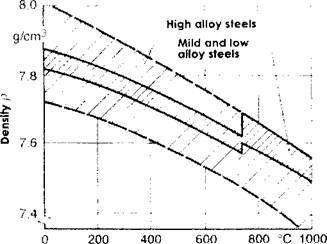
Bisra [50] and Mills [52] also present thermo-physical properties for selected commercial alloys. The thermal conductivity of steels at room temperature is reduced by increasing the amount of alloy substances, Figure 2-21. This situation is limited to the phase change temperature Al, from where the variation disappears in the slight rise of the curve.
|
a) Temperature T b) Temperature T Figure 2-21: Thermal conductivity (a) and Thermal diffusivity (b) of steels as function of temperature; from [71 and 3]. |
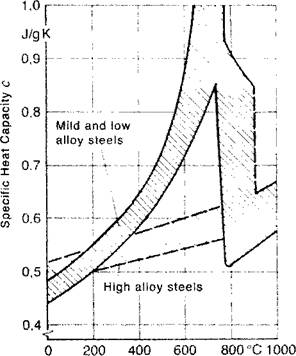
The specific heat capacity for some steels as a function of temperature is shown in Figure 2-22.
|
|
|
Figure 2-22: Specific heat capacity for some steels as function of temperature, latent heat at phase change temperature for ferrite pearlite (Al) and at phase change temperature for ferrit austenit (A3); from [71 and 3]. |
|
Temperature T |
Figure 2-23 shows the density for some steels as a function of temperature.
|
Temperature T Figure 2-23: Density of some steels as function of temperature; from [71 and 3]. |
As shown in Figure 2-9 there are four characteristic length parameters that must be determined. Physically these parameters are the radial dimensions of the molten zone in front, behind, to the side and underneath the arc. If the cross-section of the molten zone is known from experiment, these data may be used to fix the heat source dimensions. For example, the width and depth are taken directly from a cross-section of the weld. In the absence of better data, experience suggests it is reasonable to take the distance in front of the heat source equal to one-half the weld width and the distance behind the heat source equal to twice the width. If cross-sectional dimensions are not available Christensen’s expressions [48] can be used to estimate these parameters. Basically Christensen defines a non-dimensional operating parameter and non-dimensional coordinate systems. Using these expressions, the weld pool dimensions can be estimated.
The non-dimensional Christensen method was used to fix the ellipsoidal flux distribution parameters for the thick section bead on plate weld shown in Figure 2-19. The cross-sectional dimensions were reported by Chong, and the half-width dimension was applied to the flux distance in front of the electron beam heat source while the twice-width distance was applied behind the EB. The heat input fractions used in the computations were based on a parametric study of the model. Values of ff =0.6 and fr =1.4 were found to
provide the best correspondence between the measured and calculated thermal history results.
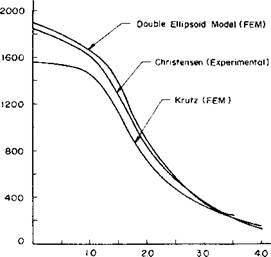
The temperature distribution along the width perpendicular to the weld center line at 11.5 seconds after the arc passed is shown in Figure 2-24 [46]. It is compared to the experimental data from Christensen et al. [48] and the finite element analysis of the same problem by Krutz and Segerlind [42] where a disc-shaped heat source (Eq. 2-4) was used. As expected, the ellipsoidal model gives better agreement with experiment than the disc.
|
Distance * IO‘z(m) Figure 2-24: Temperature distribution along the top of the workpiece perpendicular to the weld. Experimental results of Christensen [48] compared to the computed values of Krutz and Segerlind ‘disc model’ [42] and the computed values using the ‘double ellipsoid model’ [46]. |
The fusion and heat affected zone boundary positions predicted by these FEM calculations, [46], are in good agreement with the experimental data, as shown in Figure 2-16. In addition, the FEM cooling times (800 °С to 500 °С) are much closer to the experimental value than the cooling time calculated by the Rosenthal’s analysis. The FEM cooling time is slightly larger than the experimental value. This may be due to neglecting the longitudinal heat flow. The radiation-convection applied to the top surface had little effect on the thermal cycle or the FZ-FIAZ boundaries. This is to be expected for thick section welds where the heat flow is dominated by conduction.
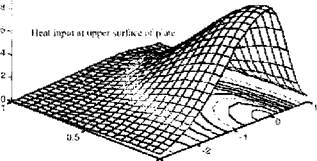
A plot of the heat input at the surface using the double ellipsoid heat source is given in Figure 2-25, from Lindgren [22].
1 a ~.
|
ФЩйШт % С* - В wtklin^ йшШіт і Figure 2-25: Heat input distribution using a double-ellipsoid heat source model, [22]. |

 Опубликовано в
Опубликовано в