1. Рассмотрим электрическую цепь, состоящую из источника

питания с ЭДС е = е sin г и последовательно соединенных дуги Д, т

индуктивности L, емкости С (конденсатора) и сопротивления R (рис. 7.1). Уравнение этой цепи имеет вид

г

е sin(r ♦ р) = x. di/dr ♦ х / Иг ♦ Л/ + и. m L с 0

Подставляя сюда (7.10), производя преобразования и приводя к удобному для расчета на ЭВМ виду, получим систему уравнений

dv/dr = [asin (г + у>) - u(cd exp by + 1) -

- vgd][d exp 6y]~' - Ми2 - 1);

_ _2 rfo/dr = и exp by; dy/dr = и - 1,

где a = e /II, d = Lx,/U,

Ш 0 L

T _

C - R/x., g = xJx., о = / h exp (by)dr.

L C L 0

Эту систему уравнений решали при следующих начальных условиях:

н(0) = 1/(0) = о(0) = 0. Неизвестные параметры <р и d подбирали так,

чтобы выполнялись условия периодичности н(я) = у(п) = 0 (при вы­полнении этих условий v(n) = 0). Если один или два элемента цепи отсутствуют, система уравнений соответственно упрощается.

1. Рассмотрим сначала случай R = Xq = 0. Результаты расчетов

для трех значений а и для различных b приведены на рис. 7.2. При

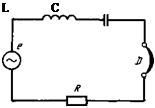Рнс. 7.1. Схема электрической цепи

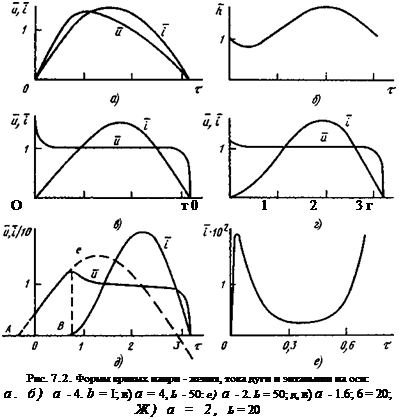
6 = 0 кривые и и і = i/l являются синусоидальными функциями, а

Л = const. В этом случае дуга ведет себя как линейное активное сопротивление. Однако, как уже указывалось, случай 6 = 0 физически нереален, поскольку соответствует бесконечно большой тепловой инерции столба дуги. При 6*0 начинают проявляться нелинейные свойства дуги как элемента электрической цепи, в частности, от­личие формы кривой и от синусоидальной тем большее, чем больше 6.

Уже при 6 = 1 форма и значительно отличается от синусоиды (рис. 7.2, а) и при увеличении 6 стремится к прямоугольной с от­носительно небольшим пиком зажигания, равным = 1,3 (рис. 7.2,

в). Форма кривой тока в данном случае остается близкой к сину­соиде, поскольку при а = 4 она в основном определяется индуктивным сопротивлением цепи. С ростом 6 увеличиваются колебания энтальпии в столбе дуги. В начале полупериода энтальпия уменьшается, не­смотря на выделение мощности в дуге (рис. 7.2, б), так как теп­ловые потери столба дуги преобладают над тепловыделением в дуге. Также объясняется уменьшение энтальпии к концу полупериода.

При а = 2, когда дуга оказывает существенное влияние на силу тока в цепи, форма кривой тока уже заметно отличается от си­нусоиды, а пик зажигания в и выражен значительно менее четко и мал по величине: ищ = 1,1 (рис. 7.2, г). Отсюда следует, что в наи­более важном в практическом отношении случае а = 3...2 (т. е. когда дуга является основной нагрузкой в цепи) не только форма кривой тока, но и величина пика зажигания зависят от а. Действительно, в рассматриваемой цепи напряжение на дуге в любой момент времени не может превысить ЭДС e(t). При а > 1, с одной стороны, > U, с

другой стороны, сдвиг фаз р -» тг/2 (влияние большой индук­тивности), т. е. в момент перехода кривой тока через нуль напря­жение на дуге достигает максимального значения е. Пик зажигания,

т

в принципе, может достигать значения е, т. е. превышать U в а раз.

При уменьшении а сдвиг фаз уменьшается и соответственно снижается максимально допустимое значение пика зажигания.

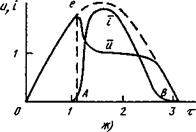
При а = 2 ток в цепи вблизи перехода через нуль весьма мал и увеличивается значительно медленнее, чем при синусоидальной форме кривой тока. На рис. 7.2, г видно сильное "затягивание” кривой тока в начале полупериода (и связанное с ним смещение максимума кривой тока к концу полупериода). Значение а = 2 является крити­ческим. При а < 2 горение дуги становится прерывистым, т. е. при большом 6 существуют отрезки времени, в течение которых сила тока близка к нулю. Рассмотрим подробнее результаты расчетов при а = = 1,6 (рис, 7.2, д, е). В точке 0 напряжение на дуге очень быстро увеличивается до ЭДС источника питания е, которая в этот момент равна e^sin <р. Ток дуги тоже быстро увеличивается (рис. 7.2, е).

Однако столб дуги к этому моменту времени уже в значительной сте­пени деионизован и проводимость его мала, поэтому значение пика тока вблизи точки 0 мало. Поскольку вблизи этой точки тепловые потери столба дуги превышают тепловыделение в дуге, проводимость столба продолжает падать и сила тока также уменьшается, несмотря на увеличение напряжения на дуге, которое в это время практически совпадает с ЭДС источника. Однако затем тепловыделение в дуге на­чинает преобладать над тепловыми потерями и сила тока увеличи­вается. Начиная с точки В, напряжение приобретает типично дуговой характер, а сила тока резко увеличивается. Таким образом, в тече­ние отрезка времени ОВ существует так называемая "пауза тока”.

2. Рассмотрим цепь, содержащую только активное сопротивление и дугу. Как и в предыдущем случае, при 6 = 0 напряжение и ток имеют синусоидальную форму, а профиль энтальпии не зависит от времени. При достаточно больших 6 горение дуги принимает прерывистый ха­рактер (рис. 7.2, ж). От начала полупериода до точки А сила тока дуги очень мала, а напряжение на разрядном промежутке практически равно ЭДС источника. В этот отрезок времени дуга представляет со­бой большое активное линейное сопротивление. Нелинейные свойства дуги начинают проявляться с точки А. Сила тока резко возрастает, напряжение на дуге уменьшается. В точке В сила тока опять снижа­ется почти до нуля, а напряжение на дуге становится равным ЭДС, т. е. с точки В и до конца полупериода сопротивление дугового про­межутка опять приобретает линейный характер. Следовательно, при горении дуги в безындуктивной (или малоиндуктивной) цепи возникает "пауза тока" В А. Длительность "паузы тока" при достаточно больших 6 зависит от а и уменьшается с увеличением а, т. е. с ростом ЭДС по сравнению с эффективным напряжением на дуге.

Рис. 7.3. Формы кривых напряжения и тока дуги в цепи с конден­сатором : О) а - 4; Ь - 5: б) * 4: Ь - 40

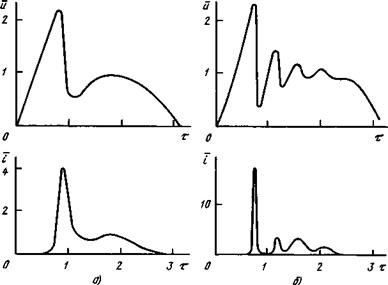
3. Пусть = R = 0, т. е. дуга включена последовательно с кон­денсатором. На рис. 7.3 приведены результаты расчетов для_а = 4. Ь = 5 и 40. В этом случае при 6*0 формы как и, так и і значи­тельно отличаются от синусоиды. При 6 » 1 на протяжении всего по - лупериода кривая и имеет колебательный характер, а ток проходит в цепи в виде отдельных импульсов, т. е. носит "искровой” характер. Это связано с периодическими зарядами и разрядами конденсатора, которые, в свою очередь, обусловлены изменениями сопротивления разрядного промежутка при изменениях силы тока дуги.

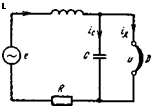
4. Большой интерес для практики представляет случай, когда дуга шунтирована малой емкостью (рис. 7.4), например емкостью токо - проводов. Соответствующие уравнения цепи имеют вид

е sin(r + <р) = xAdi/dr) + Ri + и;

Ш L

Т

І = *£ + u = «£ = *£ / t^dr; = (1 /Xfjdu/dr.

Рис. 7.4. Схема электрической цепи

Используя уравнение динамической характеристики (7.10) и производя преобразования, получим

du/dr = о; dy/dr - и - 1;

dv/dr = gfasin (т ♦ ip) - z(d exp by + f) - (7.11)

_2 —

- dft(n - l)exp by - u(dc exp by + 1)].

Краевые условия для этой системы ставятся следующим образом. Условия для и и у аналогичны рассмотренным выше:

ы(0) = й(п) = у(0) - y(tt) = 0. (7.12)

Теперь надо определить краевые условия для о. Так как и не имеет разрыва в точках 0, jt, то и <д, согласно (7.10), не имеет разрыва

в этих точках, т. е. і (0) = і (it) - 0, или і (-0) = і (+0) = 0,

д д д д

где - О и +0 означают подход к точке 0 слева и справа. Тем самым

рассматривается поведение функций в окрестности одной точки 0. Это

возможно благодаря тому, что режим считается установившимся. Если

du/dr(-0) * du/dr(0), то /^(-О) ж 1^,(0), так как <£ = (1/дг^) х

du/dr, т. е. кривая тока в емкости имеет разрыв в точке 0. Тогда кривая общего тока цепи і должна иметь разрыв в точке 0. Однако этого быть не может, так как в цепи имеется индуктивность и разрыв кривой тока і привел бы к бесконечно большому напряжению на ин­дуктивности. Таким образом, должно выполняться условие du/dr(-О) =

= du/dr(0), или du/dr(0) = - du/dr(tt). Это приводит к следующему условию для v:

о(0) = - v(it), или v(0) * v(ir) = 0.

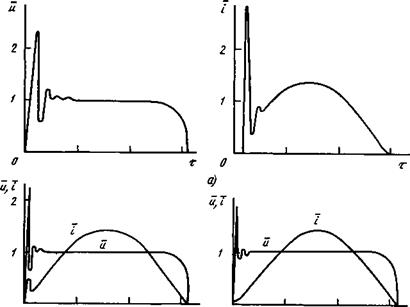
1 2 3 г О 1 Z З Г S) в) Рис. 7.5. Формы кривых напряжения и тока дуги в цепи с дугой, шунтированной конденсатором: а) а = 4; Ь - 28; g - 10; б) а = 4; Ь - 40; g = 100: в) а = 4; 6 = = 40: g = 1000

Система уравнений (7.11) решалась на ЭВМ методом пристрелки по d, <р, v(0), т. е. эти три величины подбирались так, чтобы выполнялись условия (7.12), (7.13).

На рис. 7.5 показаны расчетные кривые напряжения и тока дуги при а = 4 и различных bag. При g = 10 наблюдаются значительные колебания напряжения и тока в начале полупериода, связанные с пе­риодическими зарядами и разрядами конденсатора, причем пик напря­жения весьма велик. При g = 100 (рис. 7.5, б) пик зажигания сни­жается до и ~ 2,2, а в кривой тока наблюдается лишь единичный выброс в начале полупериода. При g = 1000 (рис. 7.5, в) кривая тока уже практически синусоидальна, однако даже в этом случае пик

зажигания еще достаточно велик (и ~ 2) и превышает и в цепи без

тп тп

емкости в 1,5 раза. Значит, шунтирование дуги очень малой ем­костью может приводить к существенному изменению кривой напря­жения на дуге.