Экспериментальное исследование теплообмена между высокотемпе­ратурным рабочим телом и стенками плазмотрона и сравнение резуль­татов экспериментов с теорией проводились путем измерения инте­гральных выходных характеристик плазмотрона (термического КПД и

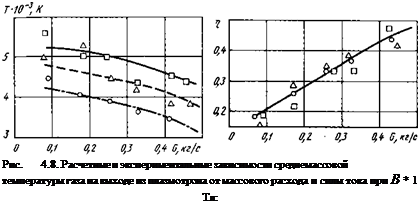Расчет Эксперимент /, А

- • ----------------------------------- о 5000

-------- Д 6000

---------------------------------------- □ 7000

Рис. 4.9. Зависимость термического КПД плазмотрона от расхода газа

при В * 1 Тл:

расчет: ------------- , / * 7000 А; эксперимент: О — / * 5000 А; А — / «

* 6000 А; □ - / * 7000 А

среднемассовой температуры рабочего газа на выходе) и локальных тепловых потоков на специальной установке.

На рис. 4.8...4.10 представлены данные экспериментов для вы­ходной среднемассовой энтальпии (температуры) и термического КПД при различных значениях силы тока, магнитной индукции в районе горения дугового разряда и расхода рабочего газа. Там же приведены для сравнения результаты расчетных данных. Они правильно описывают качественный характер зависимостей и дают удовлетворительное ко­личественное совпадение с экспериментом в исследованном диапазоне определяющих параметров. Однако существуют причины, которые могут вести к отличию теоретических результатов от экспериментальных при более широком диапазоне изменения определяющих параметров. Главные из них следующие.

1. Возможная высокая интенсивность теплоотдачи от нагретого газа за разрядом по сравнению с интенсивностью теплоотдачи, полу­чаемой на основе использования теоретических зависимостей для

Рис. 4.10. Зависимости термическо-
го КПД плазмотрона от индукции
магнитного поля и силы тока при
р * 2 МПа:

----------- расчет при / = 7 кА;

---------- эксперимент; 1 — 4,8 к А;

2 - 5,8; 3 - 6,8; 4 - 7.8 кА

0 0,5 0,75 1,0 В, Dr

»

случая течения нагретого рабочего тела вдоль стенок; увеличение интенсивности теплоотдачи может быть следствием разрушения погра­ничного слоя под действием периодического осевого шунтирования разряда.

2. Недостаточно точный расчет истинной скорости течения рабо­чего тела вдоль стенок и, в частности, использование неточного закона затухания закрутки по длине тракта плазмотрона.

Уравнение (4.32) может служить для приближенного определения w в плазмотронах с несильным затуханием закрутки по длине тракта, поскольку оно не учитывает этого затухания, но учитывает действие сил трения на осредненную скорость вращения.

Ясно, что желательно свести роль второго члена в правой части уравнения (4,32), описывающего действие сил трения, к минимуму, что можно сделать в условиях плазмотронов лишь уменьшением по­верхности S взаимодействия нагретого рабочего тела со стенками канала; при этом уменьшатся и тепловые потери в стенки, и потреб­ная величина магнитного поля для вращения дугового разряда, но, как уже выше отмечалось, из-за осевого шунтирования дуговою раз­ряда необходимо иметь некоторую протяженность камеры / . от зоны горения разряда до выхода из плазмотрона.

Оценим сравнительную роль члена, описывающего трение нагретого рабочего тела о стенку, и члена, описывающего момент количества движения, связанный с рабочим телом. Отношение этих членов

CjpwS

2G

При параметрах, характерных для коаксиальных плазмотронов, р ~ 2 МПа, S = 0,1 м2, w ~ 100 м/с, В * 0,2 Тл, G * 0,2 кг/с, D = 0,17 м, D = 0,15 м и С = 8*10 3 получаем R ~ 0,35, т. е.

К /

член, описывающий трение, одного порядка с членом, описывающим закрутку рабочею тела.

Ясно, что при увеличении поверхности плазмотрона будет воз­растать роль члена, описывающею трение, а при увеличении расхода рабочею тела роль трения, наоборот, будет падать. Для получения высоких термических КПД выгодны режимы с малым отношением Я, а для достижения максимальных выходных температур необходимо реализовать режимы, соответствующие значениям R порядка 0,1...0,15, т. е. не­достаточно точный учет трения не должен сильно отразиться на ко­нечном результате расчета А, Т, г/ при работе плазмотрона на

вых вых

режимах высоких КПД, соответствующих значениям выходной темпера­туры около 3000...4000 К, и сильнее проявится при работе плазмо­трона на режимах, соответствующих максимальным значениям выходной температуры. С целью выяснения возможного влияния указанных причин на расхождение теоретических и экспериментальных данных по выход­ной энтальпии и КПД было проведено специальное экспериментальное исследование локальной теплоотдачи от нагретого газа к стенкам плазмотрона.

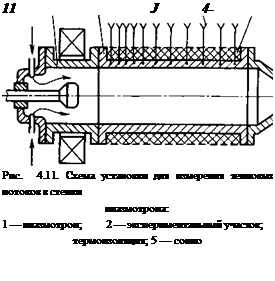В установке, схема которой приведена на рис. 4.11, эксперимен­тальный участок представляет собой неохлаждаемую теплообменную камеру, выполненную из меди с толщиной стенки 9 мм. Для снижения теплообмена стенки камеры с окружающей средой с наружной стороны камера теплоизолирована стеклотканью. Изменение давления в камере

Рис. 4.12. Схема заделки термопар

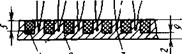в секции:

1 — термоизоляция; 2 — медная

стенка; 3 — спай термопары при постоянном расходе рабочего газа осуществлялось сменой сопел с различными размерами критического сечения.

Проводилось измерение тепловых потоков в стенку неохлаждаемого канала, который был разбит на секции. В каждой из секций в опре­деленных сечениях (см. рис. 4.11) на известную заранее глубину зачеканены термопары, по три в каждом сечении. С целью уменьшения продольных перетечек тепла секции отделялись друг от друга по на­ружной части стенок, как показано на рис. 4.12.

Время работы плазмотрона, составлявшее в этих экспериментах 0,7...5 с, выбиралось таким образом, чтобы температура стенки ка­нала в конце эксперимента была ниже того значения, при котором заметно снижается прочность материала.

По кривым зависимости температуры стенки канала от времени (нестационарный режим) рассчитывалась интенсивность теплообмена на различных участках по длине тракта. При расчете пренебрегали пере­теканием тепла по длине камеры и по окружности, а температуру в сечении определяли как среднеарифметическую величину из показаний трех термопар, зачеканенных в данном сечении.

Процесс изменения температуры стенки в определенной фиксиро­ванной точке, где зачеканена термопара, описывается одномерным уравнением теплопроводности, решение которого при граничных ус­ловиях второго рода п

N = x/S;

температура через интервал времени t; 8 - толщина стенки канала; X - коэффициент теплопроводности материала стенки; р - плотность материала стенки; с - удельная теплоемкость; х - расстояние спая термопары от наружной поверхности стенки; N - безразмерное рас­стояние.

Сигналы термопар, фиксирующих температуру стенки канала, запи­сывались на осциллографе. Изменение температуры (Г - 7^) за ин­тервал времени t определялось по осциллограммам. Зависимость ЦХ, N) затабулирована.

На рис. 4.13...4.16 представлены результаты экспериментов, вы­полненных при различных расходах рабочего тела (азота), давления в канале, магнитной индукции, силе тока в разряде, при разных рас­стояниях I от торца центрального электрода.

Тепловой поток непосредственно в зоне горения разряда не изме­рялся, поэтому в эксперименте определялось также интегральное ко-

О 100 200 300 I, мм

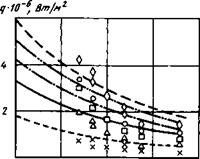Рис. 4.15. Сравнение теоретических и экспериментальных величин

плотности теплового потока при G = 200 г/с; р * 1,3 МПа; / =

» 5000 А:

Расчет

Рис. 4.16. Сравнение теоретических и экспериментальных величин

плотности теплового потока при G * 175 г/с; В * 0,6 Тл; р *

* 1,3 МПа:

Расчет ------- -------------------------------------- — -- -------------- ---------------

л л

Эксперимент х Д □ о V

/, кА 2,15 4,1 5,45 6.3 7,4 личество теплоты, ушедшее в стенки плазмотрона. На рис. 4.13... 4.16 представлены также результаты расчета распределения тепловых потоков по длине плазмотрона для различных режимов, реализованных в экспериментах. Расчеты проведены с учетом поправки на потери теплоты в центральный электрод, доразрядную и приэлектродные об­ласти электрода - камеры, т. е. в предположении, что среднемассовая энтальпия газа в плоскости торца центрального электрода опреде­ляется соотношением

Р(1 - k )/С,

Ц. ЭЛ

где значения k приняты в соответствии с рис. 4.5.

ц. ЭЛ

Видно, что интегральные потери теплоты в расчете и эксперименте вполне удовлетворительно совпадают, и это позволяет с приемлемой

степенью точности (около 15...20 %) определять значения выходной энтальпии и термического КПД. В то же время можно заметить опре­деленное систематическое расхождение между расчетными и экспери­ментальными значениями, состоящее в том, что теоретические зна­чения q завышены в области, удаленной от зоны горения разряда, в среднем на 20 % и занижены в области, прилегающей к разряду. Такое расхождение, по-видимому, является следствием более интенсивного теплообмена в областях, прилегающих к зоне горения дугового раз­ряда.