ЕДИНОЕ МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ ЭКСЕРГЕТИЧЕСКОГО К. П. Д. ЭХТС И ЕЕ ЭЛЕМЕНТОВ. ДИАГРАММА ГРАССМАНА — ШАРГУТА
 26 марта, 2013
26 марта, 2013  admin
admin Эксергетические к. п. д. ЭХТС, машин и аппаратов вычисляют по формулам (1.250) - (1.252). Нетрудно видеть, что все они по существу сводятся к единой формуле, в которой числитель представляет собой полезный эксергетический эффект, а знаменатель — затраты эксергии, следовательно, в общем случае для ЭХТС в целом и для отдельных ее элементов эксергетический к. п. д. можно вычислять но формуле
І = п І = 11
ІЕи - lDi i= 1 i=l
^ = T^n
I Eut I = 1
Существенную помощь при эксергетическом анализе ЭХТС оказывает диаграмма Грассмана — Шаргута потоков и потерь эксергии. На этой диаграмме каждый поток эксергии анализируемой ЭХТС изображается полосой, ширина которой пропорциональна значению эксергии.
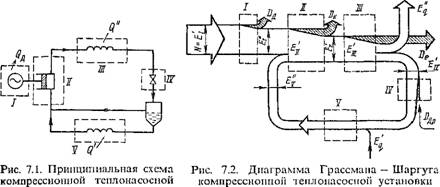
Рассмотрим принципиальную схему компрессионной теплонасосиой установки (рис. 7.1). В компрессоре II происходит сжатие паров низко - кипящего теплоносителя, после чего он поступает в конденсатор III. Здесь пары теплоносителя охлаждаются и конденсируются при высоком давлении, при этом выделяется количество теплоты Q", которое далее используется для нагрева. Из аппарата III конденсат поступает в дроссель IV, где в результате дросселирования его температура понижается. Далее охлажденный конденсат поступает в испаритель V, где за счет теплоты Q' < Q", подводимой из окружающей среды, он полностью испаряется. Образующиеся в испарителе пары теплоносителя
|
Установки |
Поступают в компрессор II, чем и завершается цикл теплоиасосной установки.
На рис. 7.2 представлена диаграмма Грассмана — Шаргута рассматриваемой компрессионной теплоиасосной установки. Здесь видны все потери эксергии в элементах установки в результате протекающих в них необратимых процессов. Величина потери эксергии в каждом элементе установки соответствует уменьшению ширины полосы эксергии и условно изображается заштрихованным треугольником, переходящим в выгнутую стрелку D, (зксергетические потери в 1-м элементе установки). В установку подводится эксергия Е'ь равная электрической мощности электродвигателя I, поскольку эксергия электрической энергии не характеризуется энтропией. В электродвигателе происходит потеря эксергии £>,„ равная сумме потерь электрической энергии в машине и приводе. Следовательно, эксергия на выходе из электродвигателя Е{' = Е'і — 1>л. Эксергия па входе в компрессор Е{ — Е{' + Е'{,, Где Ј'v — эксергия паров теплоносителя, выходящего из испарителя V. Эта суммарная эксергия преобразуется в компрессоре в эксергию сжатых паров теплоносителя. Эксергия на выходе из компрессора Ці = Ці — где DK — зксергетические потери в компрессоре, причем DK » Dn. Очевидно, эксергия на входе в конденсатор £{и = Ец. В конденсаторе будет потеря эксергии De, связанная с теплопередачей при конечной разности температур между теплоносителем и внешним приемником теплоты и поэтому эксергия на выходе из конденсатора - Єні = Е'т ~ £>е - Большая часть JEj этой эксергии отдается потребителю в виде теплового потока повышенной температуры; другая часть, равная Ет — Е"(, — Е{у, есть эксергия на входе в дроссель IV. При дросселировании теплоносителя возникает потеря эксергии от необратимости процесса ДцР, вследствие чего эксергия на выходе из дросселя Efv = Јiv — Дцр. Эксергия на входе в испаритель Е' = Е[' + Е'ф где E'Q — Эксергия теплового потока, подводимого в испаритель из окружающей среды; ее значение E'Q = (?' (1 — 7о/ТІ)« 0, так как Ті ss Т0. По этой же причине и потери эксергии в испарителе иа конечную разность температур также будут близки нулю. Следовательно, эксергия на выходе из испарителя JEV = Ј'v - § 7.3. ВИДЫ ЭКСЕРГЕТИЧЕСКИХ ПОТЕРЬ
Определение потерь эксергии, не характеризуемой энтропией, не представляет трудности, поэтому в настоящем параграфе рассматриваются потери тех видов эксергии, которые характеризуются энтропией. Рассмотрим эти потери.
Потери эксергии в теплообмен и ом аппарате DK В общем случае представляют сумму четырех потерь, вызванных конечной разностью температур £>т, гидравлическим сопротивлением Dp, Теплообменом с окружающей средой £)ос и теплопроводностью вдоль теплообменника. Так как обычно в теплообменниках ЭХТС последние потери весьма малы, то ими пренебрегают, следовательно;
DTe = DT + Dp + Doc. (7.2)
Потеря эксергии в теплообменнике от конечной разности температур
DT = EJ - E[6] = твечв - MAeqA = £ 64 ДтЕ = Q ДтД (7.3)
Где Eq и Eq — эксергии тепловых потоков теплоносителей В и А соответственно; тв и тА — массы теплоносителей В и А соответственно; EqВ и EqA — удельные эксергии тепловых потоков теплоносителей В и А Соответственно.
Так как вычисление Dr при переменных температурах связано с большими трудностями, то следует воспользоваться выводом формулы (1.241), поскольку в теплообменниках ЭХТС процессы протекают практически при постоянном давлении. Следовательно, вместо формулы (7.3) можно написать, что
Dг = - = MBeqB - тле(,а = >»в Аев - тА Аел, (7.4)
Где Аев и АеА — изменение потоков эксергии теплоносителей В и А Соответственно.
Для теплообменника, в котором теплообмен протекает при фазовых превращениях, т. е. при постоянных температурах Тв и ТА, например в кипятильниках-конденсаторах, потери DT могут быть вычислены по формуле
D r = JE? - E:I = QxeB - QieA = Q (X® - Те) =
ЧМН'-вЬЧіЧ} '
Формула (7.5) применима для любого теплообменника, если переменные температуры каждого теплоносителя заменить на средне - интегральные значения Тв и ТА.
Из вышеприведенных формул следует, что чем меньше температурный напор теплообменника, тем меньше будет в нем основных потерь эксергии — потерь от конечной разности температур.
Потери эксергии от гидравлических сопротивлений Dp обусловлены движением теплоносителей в теплообменнике. Если бы движение теплоносителей было без трения, то Dp = 0. Так как работа, затрачиваемая на движение теплоносителей в теплообменнике, равна работе нагнетательных устройств (компрессоров и насосов), то, очевидно,
Dp = La + LB, (7.6)
Где La И Lb — техническая работа нагнетателя теплоносителя А и теплоносителя В соответственно.
Потери эксергии от теплообмена с окружающей средой D0.C имеют место при теплообмене тепловой изоляции машин и аппаратов с окружающей средой (То). Следовательно, потери эксергии от несовершенства тепловой изоляции D0. с определятся по формуле
Do. с = ТАЄц + ТвЄд = MAqAxcA + твцвъ? в = = MAqA ( 1 - + MBqe ( 1 - (7.7)
іиз/1 / ImB J
Где QA и QB — плотности тепловых потоков от теплоносителей А и В Через тепловую изоляцию в окружающую среду или наоборот (когда температуры теплоносителей меньше температуры окружающей среды Т0); ТтА и ТтВ — среднеинтегральные температуры внешней тепловой изоляции теплоносителей А и В соответственно. Из формулы (7.7) следует, что когда Тт-*Т0, то Do C-+ 0.
Потери эксергии в реакторе от протекания в нем химической реакции £>х. р можно подсчитать, исходя из формулы (1.207). Рассмотрим экзотермическую реакцию, протекающую при постоянных температуре и давлении. Теплота реакции передается какому-либо телу, которое находится при той же температуре. Тогда изменение энтропии в химическом реакторе составит
Asx, p = As + AsT,
Где As и AsT — изменение энтропии системы, в которой протекает реакция, и другого тела соответственно.
Если работа, обусловленная изменением объема системы при постоянном давлении, совершается только в результате реакции, то теплота, передаваемая другому телу, будет равна уменьшению энтальпии этой системы, т. е. (-АН) и поэтому указанное выше уравнение может быть записано так:
Asx. p = - Д5 + (АЯ/Т) = (- TAs + АН)/Т— AZ/T (7.8)
И потери на необратимость, так называемые зксергетические потери
= TqAs^P = TQAZ/T. (7.9)
|
313 |
Следовательно, энтропия, созданная в химической реакции, происходящей при постоянных температуре и давлении, равна изменению изобарно-изотермического потенциала, деленному на температуру, при которой происходит реакция, а эксергетическая потеря этого процесса — произведению энтропии на температуру окружающей среды.
12 А. В. Чечеткин, Н. А. Занемонец
Потери эксергии в тепловых машинах, компрессорах и насосах находятся непосредственно из эксергетического баланса, составленного для данной машины. Этот вопрос подробно рассмотрен в § 7.7.

 Опубликовано в
Опубликовано в