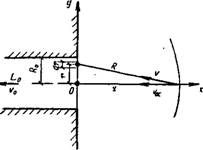
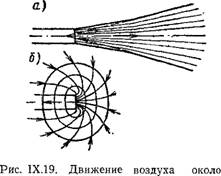
Картина движения воздуха около вытяжных и около приточных отверстий совершенно различна. При всасывании воздух подтекает к от­верстию со всех сторон, а при нагнетании он истекает из отверстия в виде струи с углом раскрытия примерно 25° (рис. IX. 19).

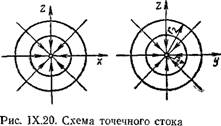
Рассмотрим чисто теоретическое понятие точечного и линейного сто­ков. Представим точку в пространстве, через которую в единицу време­ни удаляется количество воздуха L. Воздух к точке, очевидно, подте­кает из всего окружающего пространства по радиусам (рис. IX.20). Ра­диусы будут являться линиями тока. Через сферические поверхности радиусом г в единицу времени будет протекать (стекаться к точке) та­кое же количество воздуха, какое удаляется через точку, т. е. L. Сфе­рические поверхности Fx, F2,..., Fn будут поверхностями равных скоро­стей v2,...,vn. Расход воздуха через точку можно представить через расходы на сферических поверхностях:

L = /?! oj = F2 v2 = • • • = Fn va

Или

4 яг J Oj = 4 zir v2 =• • • = 4 nr* vn,

Отсюда

R2

Pi_____ [2_

~ r

9—425

Т. е. при точечном стоке воздуха скорости изменяются обратно пропор­ционально квадратам радиусов.

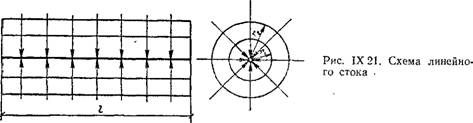
При линейном стоке удаление воздуха происходит через линию бес­конечно большой длины (рис. IX.21). В этом случае поверхностями рав­ных скоростей будут боковые поверхности цилиндров Fh F2,..., Fn радйу-

Приточного (а) и вытяжного (б) отвер­стий

Сом rh г2,..., гп. Расход воздуха через линию равен расходу через лю­бую цилиндрическую поверхность:

L = 2nr1lv1 = 2лг2/у2 ==•■•= 2:xrnlvn,

Отсюда

(IX. 43)

Т. е. при линейном стоке воздуха скорости изменяются обратно пропор­ционально радиусам.

Понятия точечного и линейного стоков позволяют дать качествен­ную оценку движения воздуха около реальных вытяжных отверстий круглой и щелевидной формы, а также, в первом приближении, оценить распределение скоростей движения воздуха около этих отверстий.

Экспериментальные исследования распределения скоростей около всасывающих отверстий показали, что действительная картина поля скоростей вблизи отверстия заметно отличается от определенной по стокам. Достаточное для многих практических расчетов совпадение на­блюдается на расстоянии от отверстия или х^2В0, где d0 — диа­метр круглого отверстия, 2В0 — ширина щелевого отверстия.

При щелевидных отверстиях большое влияние на распределение скоростей оказывают торцы щели, так как в этих местах движение воз­духа более похоже на точечный сток, чем на линейный.

Вблизи вытяжных отверстий конечных размеров закономерности те­чения воздуха зависят от формы отверстия и соотношения его сторон.

Закономерности движения воздуха около всасывающих отверстий исследовались многими отечественными и зарубежными авторами. Ни­же приводятся аналитические исследования И. А. Шепелева для, стока воздуха в круглое отверстие и в узкую щель.

Через круглое отверстие радиусом R0 в плоской стенке удаляется воздух со скоростью v0 в количестве L0 (рис. IX.22). Определим ско­рость на оси симметрии стока v0c• Выделим в плоскости отверстия эле­ментарную площадку dF, образованную пересечением дуг концентриче­ских окружностей и радиусов. Если угол между радиусами dtp, а рас­стояние между окружностями dr, то площадь элементарной площадки, находящейся от центра отверстия на расстоянии г, выразится равенст­вом dF = rdydr.

Элементарный расход воздуха через площадку dF вызовет элемен­тарную скорость воздуха в пространстве около отверстия. Полагая, что поле равных скоростей около отверстия представляет собой половину сферической поверхности радиуса R, можем записать равенство

V0 rdffdr = 2nR2 dv, (IX. 44)

Откуда элементарная скорость

Элементарная скорость на оси стока

Dvoc^dv~-. (IX. 45)

R

Имея в виду, что R= (x2+f2)1/2, зависимость (IX.45) можно запи­сать в виде. (

2л (JC2+rzf/a

Интегрирование этого выражения по углу <р в пределах от нуля до 2я и вторично по радиусу г в пределах от нуля до RQ дает значение ско­рости на оси симметрии потока:

Foe = "о / 1 --------------------------------------------- 1 • (IX.47)

Для щели задача о стоке приведена на рис. IX.23. Через длинную щель шириной 2В0 удаляется воздух в количестве L0 со скоростью у0 Определим компоненту скорости вдоль оси х в произвольной точке про­странства перед щелью. Считаем, что линии тока образующегося тече­ния направлены по кратчайшему пути к всасывающей щели. Разделим всасывающее отверстие — щель — на бесконечно тонкие полоски дли­ной, равной длине щели, и шириной db. Одна из таких полосок нахо­дится на расстоянии b от начала координат, которое совпадает с цент­ром щели. Через элемент щели площадью dbl0 будет отсасываться эле­ментарный объем воздуха dL — dbloVQ, который вызовет элементарную скорость воздуха dv в точках пространства. Поле равных скоростей бу-

	У - / / / / / //////	Jf*	V*const
J-a	I-O		X	9 X
"о
/ ✓ / /

Рис. IX.22. Сток воздуха в круглое отвер - Рис. IX.23. Сток воздуха в длинную стие щель

Дет представлять собой половину боковой поверхности цилиндра радиу­са R, и, следовательно, будет справедливо равенство

DL — nRl0 dv. (IX.48)

Так как элементарный расход dL может быть представлен через

Общий расход воздуха в щели dL= L° dblQ, то элементарная скорость

2 В0 10

V - const

Dv запишется в виде

L0

Dv =

2nl0 Bo R

■db.

Компонента скорости в направлении оси хз

(IX. 49)

Х

Dvx = dv •

R *

Поскольку расстояние от рассматриваемой точки до элементарной полосы R = [*[5]+ (у—Ь)2]1/г, зависимость (IX.49) примет вид •

И. А. Шепелевым получены также расчетные зависимости и для других случаев стока воздуха.

Экспериментально исследованы всасывающие отверстия различной формы: круглые, квадратные, прямоугольные и щелевидные с различ-

Ным соотношением сторон. Для этих отверстий получены поля скоро­стей всасывания. Спектры скоростей всасывания в отношении числа Re считаются автомодельными.

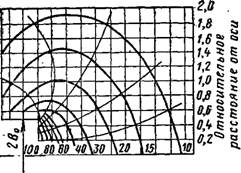
На рис. IX.24 приводится спектр скоростей всасывания у круглого отверстия с острыми кромками, в котором скорости отнесены к скорости в центре отверстия. Из рис. IX.24 следует, что на расстоянии x=l,03do скорость движения воздуха составляет всего 5% скорости в центре от­верстия. Для сопоставления отметим, что в приточной свободной круг­лой струе такое же соотношение скоростей на оси струи t»oc/foa=0,05

Наблюдается на расстоянии хж «ЮО^о. Кривые распределения относительных скоростей несколь­ко вытянуты и более похожи на дуги эллипса, чем на окружности, Спектр скорое - и только на расстоянии x>do теи всасывания г

У круглого от- сравнительно хорошо описывают-

О 0.2 OA 0,6 0,81,0 x/d0

Ми

Верстия с ост - ся окружностями с центром, на - рыми кромка- ходящимся примерно в центре всасывающего отверстия. Даль­нейшее изменение скоростей во

W^W 1,0 1,21,<t 1.6 US 2.8 x/ZBo

7 Х/А

Рис. IX.26. Кривые затухания осевых скоростей при различной форме всасы­вающего отверстия

Фронтальной части перед отверстием приближенно можно вычислять по закономерностям точечного стока.

Спектр скоростей всасывания для отверстия квадратной формы ма­ло отличается от спектра для круглого отверстия. Так, если для круг­лого отверстия иосМ)ц=0,05 оказывается на расстоянии *=l,03do, то для квадратного — на расстоянии 1,2^-2В0.

Зона всасывания у вытяжных отверстий прямоугольной формы ока­зывается более активной, чем у круглых или квадратных отверстий, так как такие отверстия по форме приближаются к линейному стоку и тем больше, чем больше соотношение их сторон.

На рис. IX.25 приведен спектр скоростей всасывания у прямоуголь­ного отверстия с острыми кромками с соотношением сторон 1 : 10. В этом случае на расстоянии х=2В0 скорость уос ~ 0,22иоц, т. е. почти в 4,5 раза больше, чем для круглого отверстия при x = d0.

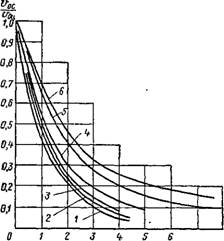
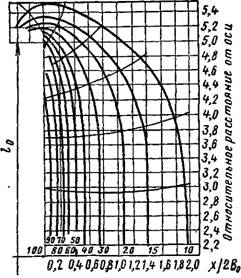
Если относительные расстояния выразить не через линейный раз­мер отверстия, а через гидравлический радиус х/А, то распределение скоростей у всасывающего отверстия можно представить на одном графике. Такой график для отверстия с острыми кромками приведен на рис. IX.26; здесь по оси ординат отложены относительные скорости Uoc/аоц (отношение скорости в рассматриваемой точке на оси к скорости в центре отверстия), а по оси абсцисс — относительные расстояния xjA (отношение расстояния от плоскости всасывания до рассматриваемой точки к гидравлическому радиусу отверстия).

§ 46. СХЕМЫ ДВИЖЕНИЯ ВОЗДУХА

В ВЕНТИЛИРУЕМЫХ ПОМЕЩЕНИЯХ

Чтобы правильно расположить отверстия для подачи воздуха в по­мещение и для удаления его, необходимо выяснить влияние взаимного расположения этих отверстий на движение воздуха в помещении.

При рассмотрении свободной струи установлено, что количество воздуха в струе непрерывно увеличивается по мере удаления рассмат­риваемых сечений от приточного отверстия, а подтекание воздуха из окружающего пространства происходит по всей длине струи и охваты­вает некоторый контур «замкнутой системы» (см. рис. IX.3). Заметим, что количество воздуха в струе при равномерном начальном поле ско­ростей на расстоянии, например, х = 40^0 будет в 6,2 раза больше по­данного через приточное отверстие [определено по формуле (д) табл. IX.1], т. е. объем воздуха, присоединившегося к струе из окружаю­щего пространства, составляет 5,2L0.

В помещении, в котором приточное и вытяжное отверстия располо­жены в противоположных торцовых стенах, при балансе притока и вы­тяжки (имеется в виду достаточно большое помещение, в котором струя распространяется как свободная) оказывается, что только 16% пере­мещаемого воздуха будет» удалено через вытяжное отверстие, а осталь­ные 84% не будут удалены и пойдут на питание струи.

В помещении конечных размеров неудаляемая через вытяжное от­верстие часть воздуха струи образует обратный поток, направленный к началу струи (рис. IX.27).

Заметим также, что затухание скорости около вытяжных отверстий происходит весьма интенсивно, и на расстоянии x = d0 скорость состав­ляет всего около 5% начальной скорости, т. е. их~0,05и0. Из этого сле­дует вывод, что скорости воздуха в вытяжных отверстиях не могут ока­зывать существенного влияния на скорости движения воздуха в поме­щении. Однако это совсем не означает, что положение вытяжного
отверстия в помещении ire оказывает никакою влияния на направление движения воздуха.

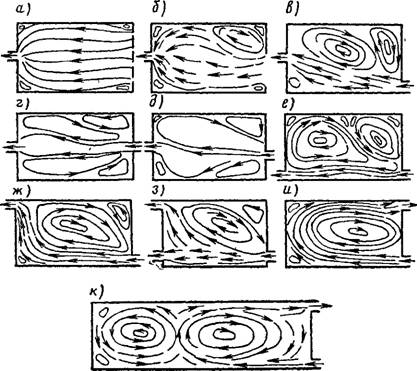
На рис. IX.28 представлены схемы движения воздуха в помещении, полученные В. В. Батуриным и В. И. Ханженковым [7] на плоской и частично на пространственных моделях. Эти схемы дают возможность составить качественное представление об организации общеобменной вентиляции в помещении. Количественные зависимости для струй, рас­пространяющихся в ограниченном пространстве, и для спектров всасы­вания приведены в предыдущих параграфах.

1ШШШ

( Рис. 1X28. Схемы движения воздуха в венти­лируемом помещении (

Рис 1X27 Схема взаимодействия приточной струи и спектра всасывания

На схеме а воздух удаляется через отверстие в середине торцовой стенки; противоположная торцовая стенка отсутствует и через этот про­ем поступает воздух. При поступлении воздуха на кромках происходит некоторое поджатие струи и образуются небольшие области, заполнен­ные вихрями; далее поток выравнивается и двигается к вытяжному от­верстию, заполняя все сечение модели; при обтекании углов образуют­ся небольшие вихревые зоны; обратных потоков воздуха нет. Во всех остальных схемах организации воздухообмена наблюдаются обратные потоки воздуха. На схеме и, в которой вытяжное и приточное отверстия
расположены в одной торцовой стенке, весь поток воздуха поворачи­вается в сторону вытяжного отверстия; при этой схеме достигается наилучшее распределение воздуха в помещении. При большой длине помещения (схема к) струя, не достигнув противоположной стены, рас­палась и в помещении образовалось два кольца циркуляции.

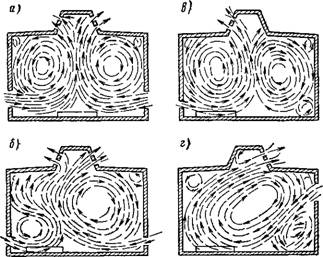
Рис. ІХ.29. Схемы циркуляции потоков воздуха в помеще­нии при неизотермических условиях

Схемы распределения потоков воздуха, приведенные на рис. ІХ.28, относятся к изотермическим условиям. Представление о циркуляции потоков воздуха в помещении при неизотермических условиях и при на­личии источников тепловыделений могут дать схемы, приведенные на рис. ІХ.29. Эти схемы получены В. В. Батуриным по результатам опы­тов на пространственной модели однопролетного производственного кор­пуса.

Схемы а, б я в относятся к теплому периоду года, когда поступление приточного воздуха при аэрации помещения происходит через открытые фрамуги в рабочей зоне; схема г относится к холодному периоду с по­дачей приточного воздуха через фрамуги в верхней зоне помещения.

На рис. ІХ.29, а источники тепловыделений занимают среднюю часть помещения, а приточный воздух поступает с двух сторон из от­верстий в противоположных стенах. Когда объемы приточного воздуха, подаваемого с каждой стороны, равны, ось тепловой струи вертикальна и является осью симметрии образующихся двух колец циркуляции.

Если приблизить источники тепловыделений к одному из приточ­ных отверстий (рис. ІХ.29, б), то тепловые струи, возникающие над ис­точниками тепловыделений, будут несколько препятствовать поступле­нию струи приточного воздуха слева — произойдет взаимодействие струй: тепловой и приточной. Струи, вливающиеся справа и свободно развивающиеся, также отклоняют тепловую струю влево.

Схема потоков, приведенная на рис. ІХ.29, в, наблюдается при сме­щенных источниках тепловыделений, но при поступлении приточного воздуха только со стороны источников. В этом случае тепловая струя оттесняется к середине. Образуются два кольца циркуляции.

В холодный период года неподогретый приточный воздух может по­даваться через створки на высоте не менее 4 м от пола. Опускающаяся струя (рис. IX.29, г) разветвляется у пола и образует два кольца цир­куляции. В правом обособленном кольце циркуляции наблюдаются по­ниженные температуры но сравнению с левым большим кольцом, в ко­торое поступает тепловая струя.