Необходимость разработки прецизионных измерителей угловых перемещений связана с рядом технических проблем, например из области геофизики, астрономии, где в последнее время все большее значение приобретают автоматические программные і стабилизи­рующие устройства повышенной точности.

Особую сложность представляет задача построения прецизион­ных измерителей малых угловых перемещений на уровне единиц угловых секунд или ее долей. При этом возможность преобразования подобных угловых величин в код или частоту следования импульсов в значительной степени определяет возможность дальнейшего улуч­шения показателей большого числа устройств,, используемых в раз­личных областях техники.

Известные принципы построения прецизионных преобразователей типа угол — код, основанные на использовании кодовых дисков [Л. 29, 38], имеющих непосредственную связь с контролируемым объектом, не свободны от нестабильности работы считывающих устройств. Они характеризуются весьма сложной технологией про­изводства кодовых дисков при числе разрядов более 17—18. Пре­образование угловых перемещений менее? одной угловой секунды требует использования дисков с числом разрядов более 20.

Рассмотрим прецизионные угловые преобразователи без исполь­зования считывающих устройств и кодовых дисков на основе маг­нитных квантовых датчиков частотного типа. В подобных устрой­ствах, как мы видели, частота на выходе пропорциональна напря­женности постоянного магнитного поля Н в зоне датчика:

f = klH + k2H (2-1)

где kit k2 — постоянные преобразования, определяемые атомными константами [в слабом поле 10-5&i, см. формулу (1-51)].

Для цезиевого датчика константы k и k2 таковы, что в ноле Земли (#=40 а/м) частота на его выходе близка к 175 кгц.

Счет импульсов с частотой / в течение определенного времени позволяет при необходимости 'получить цифровой код напряженности магнитного поля Н.

Ниже описан дифференциальный вариант подобного устройства, свободный от недостатков, связанных с вариациями магнитного поля Земли, и имеющий для рассматриваемого случая преобразования малых углов линейную характеристику преобразования.

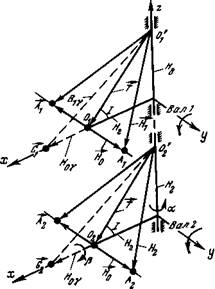
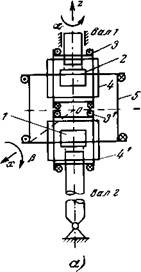
углового положения в код. Здесь показаны вектор опорного магнит­ного 'поля Т в точках 0 и 0'2, принадлежащих центрам идентич­ных квантовых датчиков. Датчики расположены в двухкомпонентных кольцах Гельмгольца, которые укреплены на валах / и 2 (поз. 3 и 4, 3' и 4'). Q помощью контуров 3 и 3' создаются магнитные поля

H0t параллельные оси у (ОіЛі и 02Л2), а контуры 4 и 4' ориентиро­ваны по оси х (ОіСі и 02С2) и возбуждаются поочередно с контура­ми 3 и 3'. Магнитный контур 5, общий для обоих квантовых датчи­ков, используется для создания дополнительного поля по оси г. Этот контур, как показано ниже, необходим для повышения точности работы преобразователя и контроля изменений всех трех углов а, р, у, характеризующих взаимное положение валов / и 2. Результи­рующие векторы магнитного поля в каждой точке обозначены через

/Лий.

S ум. сен

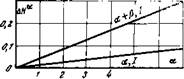
Рис. 2-2. Зависимость приращения модуля магнитного поля от изме­нения угла.

На рис. 2-2 показано, что в реальных прецизионных кон - га&леы струкциях при преобразовании W малых угловых перемещений неидеальность опор валов и на­личие незначительных углов Ар и Ду весьма существенно сказываются на точности пре­образования угла Аа в код.

Здесь для частного случая аїри,

Т=5.104 гамму Яо=104 гамм,

7=72° вычислены значения раз­ности модулей векторов по ф. о-рмуле (2-2) (кривые с шара

метрами а, I) и величина разности модулей Н и Яг при наличии разворота как по углу а, так и по углу Р (кривая а+Р, /) при а=р.

Степень изменения величины АИа в функции от Аа, а Аот Af столь велика, что^для разделения сигналов по углам аир (или р и y) необходимо применить специальную методику.

Так, используя соотношения (2-2) и (2-3), можно найти, что при контроле углов а и р и определенных значениях величин Яг

А//? = (‘^")1Ав+('1г')1А?* (2-5)

а при измененном значении составляющей опорного поля ЯВ=ЯВі (за счет подачи тока в магнитную систему 5)

(2-6)

Значения приращений углов Аа и Ар здесь приняты неизмен­ными.

Соответственно при контроле угла у

(2-7) (2-8)

дН да

4Н1 “ (тг-),4 * + (тг-),41;

)44*+(-зг)л

—

/ дН ( дН ( дН

где

I —fa— I > 1 “jjp—J —J —частные производные от выра­жений (2-2) — (2-4) по координатам а, р, f при исходном и изменен­ном значениях составляющей //, до уровня Ня1.

При составлении уравнений (2-5) — (2-8) учтено, что изменение угла у Для рассматриваемых небольших смещений практически не сказывается на изменении сигнала по углам а и р, а вариации угла р не приводят к изменению сигнала по углу у.

Пусть каждый из сигналов получен при определенном значении тока в контуре 5 (например, нулевом и значении тока, компенси­рующем вертикальную составляющую магнитного поля. Нв в зоне датчиков 1 и 2 на 50%). Тогда, решая совместно уравнения (2-5) и (2-6), можно получить полное разделение сигналов в каналах а и р.

ДВух кзантобых датчиков 1 и 2 при выключенной компенсационной магнитной системе 5.

В соответствии с формулой (2-1) разность частот окажется рав­ной:

A/ = kxLH* + k2 (АИ*)* + 2k2HAHa, (2-12)

где

Н = VHl+ НІ + НІ.

При преобразовании углов менее 15—20 угл. сек и методической погрешности преобразования менее 0,001% можно использовать упро­щенную формулу

Д/ = М Яа, (2-13)

из которой вытекает линейность зависимости между частотой А/ и углом Да:

ДЯа Д//аЯ ЯД/

А“_ (ШЛ ~ ( >

(да)

Из формулы (2-15) следует, что в согласованном положении валов (при Да=0) погрешность преобразования определяется точ­ностью определения разности частот. Расчеты по формуле (2-15) показывают, что при угловых перемещениях валов порядка не­скольких единиц угловых секунд погрешность преобразования опре­деляется в основном величиной последнего слагаемого.

Так, при использовании в преобразователях контуров со сла­быми магнитными полями, близкими к величине магнитного поля Земли, производная да,/д[ близка к 2,5 • 10-6. В этом случае дис­персия контролируемой частоты ®д^=1 гц приводит к дисперсии по углу 0у5 угл. сек (1 угл. сек=6-~в). Однако возможности си­стем автоматического контроля частот значительно шире.

Производная da/df имеет наименьшее значение при Я = У //q + Яр, поэтому максимальная точность работы, например

ііри преобразовании угла а Достигается путем полной компенсаций бертикальной составляющей поля с помощью контура 5 (см. рис. 2-1). Если при этом выполняется условие #о»#г, то в соответ­ствии с формулой (2-16) имеем:

(2-17)

Разрешающая способность преобразователя определяется по­грешностью системы автоматического контроля частоты и чувстви­тельностью квантового датчика.

В квантовых преобразователях для преобразования частоты в код целесообразно использовать специальные приемы обработки частотной информации. Определенные преимущества здесь имеют автоматические системы, построенные на принципе импульсных бие­ний, где увеличение быстродействия и точности преобразования мо­жет быть получено за счет резкого уменьшения периода частоты биений, достигаемого использованием схемы совпадения и высоко­частотной эталонной «последовательности импульсов (см. гл. 4).

С учетом дисперсий системы контроля частоты разрешающая способность преобразователя может быть вычислена по формуле

°амИН Htkx ’ (2“18)

С другой стороны, разрешающая способность дифференциального преобразователя ограничена чувствительностью квантового измери­теля (АЯмин). Тогда

ЬН мин

(2-19)

, МИЛ

0 амин дИ/да

и при чувствительности дН/да 0,01—0,02 гамм/угл. сек, что имеет место в полях, близких к уровню земного магнитного поля, расчетное значение оамин составляет несколько сотых долей угловой секунды.

(В ряде случаев весьма удобным для автоматической записи угловых перемещений оказывается режим синхронизации частот двух датчиков, разработанный В. А. Прищепо и О. II. Хвостовым. В этом случае частота квантового датчика 1 (см. рис. 2-1) будет прибли­жаться к частоте второго (возмущенного) датчика и разница частот устраняется за счет появления приращения поля АН0 в зоне этого датчика, создаваемого током в цепи синхронизации:

(2-20)

где у — гиромагнитное отношение для рабочего вещества ядерного датчика или константа ki квантового датчика; G—магнитная по­стоянная колец Гельмгольца системы синхронизации[6]; R0.с—сопро­
тивление колец Гельмгольца; и0.«—напряжение на клеммах этих колец.

Напряжение на выходе дискриминатора системы синхронизации Uy пропорционально сдвигу по фазе между векторами выходных напря­жений квантовых генераторов:

% =£mf(?l— ?2)=£mf(¥), (2-21)

где - фі и iq>2 — начальные фазы сигналов квантовых датчиков; Ет— максимальное напряжение на выходе фазового дискриминатора.

Напряжение на выходе дискриминатора фильтруется и поэтому оно связано с напряжением на выходе фильтра уравнением

di£r% р

и*=Т*-$Г + и о. о. (2-22)

где 7'ф — постоянная времени фильтра.

Поэтому в состоянии равновесия между выходными напряжения­ми датчиков устанавливается фазовый сдвиг, определяемый по функ­ции /(, ф):

* , , («і — ®г) Яо. с

f(t)= п (2-23)

гВ уравнениях (2-20) — (2-23) не учтена инерционность спиновой системы. При малой постоянной времени фильтра время установле­ния определенного уровня сигнала в цепи синхронизации определя­ется в основном временем поперечной релаксации Т*2.

Это является важным обстоятельством, и при чрезмерно ма­лых угловых перемещениях и соответственно очень малых отклоне­ниях частоты удается, не прибегая к счету импульсов, оценить ве­личину угла по уровню тока в цепи синхронизации. Этот ток может быть зарегистрирован, например, с помощью электронного потенцио­метра.

Таким образом, на выходе квантовых измерителей формируется сигнал, частота которого определяется значением атомных констант и уровнем магнитного поля в зоне датчика, функционально связан­ным с изменениями углового положения контролируемой системы.

Разрешающая способность квантовых измерителей может пре­восходить разрешающую способность, достигнутую в известных устройствах на основе кодовых дисков, на два-три порядка. Основ­ную погрешность преобразования при этом, как следует из соотноше­ния (2-15), вызывает система автоматического измерения частоты, к быстродействию и точности которой предъявляются повышенные требования.

В дифференциальной конструкции преобразователя достигается существенное ослабление влияния вариаций внешних магнитных по­лей. Практически полная компенсация помех может быть достигнута при использовании малогабаритных квантовых датчиков, уменьшении базового расстояния преобразователя или использовании ферромаг­нитных экранов. В 'последнем случае может оказаться целесообраз­ной обычная, а не дифференциальная схема преобразователя.

Использование достаточно простых алгоритмов позволяет путем повторного измерения сигналов на выходе преобразователя исклю­чить розможные погрешности из-за перекрестного влияния каналов (влияния вариаций угла р при измерении углов а или углов — при измерении угла Р).

Соотношения (2-9) и (2-10) позволяют получить информацию об изменении пространственного положения оси контролируемого ва­ла. Указанная информация может быть использована также в пре­цизионных устройствах для слежения за угловым положением, когда разрешающая способность известных измерителей оказывается недо­статочной.