Bimolecular rate equations for quantum well structures
 2 марта, 2014
2 марта, 2014  admin
admin Quantum wells provide a means of confining the free carriers to a narrow quantum well region by using the two barrier regions cladding the quantum well. Assume that the well region has a thickness of LqW. Assume further that the conduction band and valence band wells have carrier densities of n2D and p2D, respectively. The effective three-dimensional (3D) carrier concentration for electrons and holes can be approximated by n2D / LqW and p2D / LqW, respectively. Using these values as the 3D carrier concentration, the recombination rate can be inferred from Eq. (2.5), and it is given by
n2D p2D
R = B---------------- ^------- . (2.20)
lqw lqw
This equation illustrates one of the essential advantages of quantum well and double heterostructures. A decrease of the quantum well thickness allows one to attain high 3D carrier concentrations (carriers per cm3). As a result, the carrier lifetime for radiative recombination is reduced, as inferred from Eq. (2.11), and the radiative efficiency is increased.
For sufficiently small quantum well thicknesses, the wave function no longer scales with the physical well width. LqW must be replaced by the carrier distribution width, which for sufficiently small well thicknesses is larger than LqW, since the wave function will extend into the barriers. This effect should be considered for well thicknesses < 100 A in the AlGaAs/GaAs material system.
2.2 Luminescence decay The carrier decay in semiconductors can be measured by the decay of the luminescence after a short optical excitation pulse. The luminescence intensity is proportional to the recombination rate. Calculating the recombination rate for the low and high excitation cases (Eqs. 2.9 and 2.17), one obtains
R = _ dn(t)
dt and
R = - d"(t) dt
А "
—— e-t 'т for low excitation (2.21)
T
- B
- for high excitation. (2.22)
Bt + А"0-1)
|
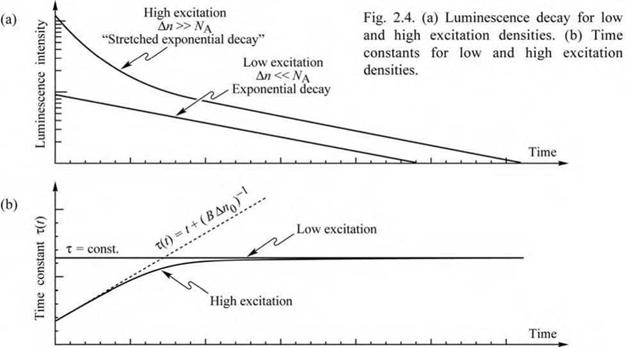
Figure 2.4 illustrates schematically the decay of the luminescence after optical excitation by a short pulse. For the case of low excitation density, the decay is exponential with a time constant т. For the case of high excitation, the decay is non-exponential. All non-exponential decay functions can be expressed by an exponential function with a time-dependent time constant, i. e. exp [ - t/x(t) ]. In most cases, the time constant т increases with time. This type of decay function is frequently called a stretched exponential decay function which describes a slower-than-exponential decay.
|
A particularly well-known stretched exponential function is given by exp { - [ t/x(t) ]e }, where P, the disorder parameter, represents the disorder of the radiative material. For в = 1, no disorder exists in the material. For в « 1/2, a strong disorder exists in the material and such values of в have been found in glasses (Phillips, 1996) as well as semiconductors. Nonexponential decays were first discovered and discussed by Friedrich Kohlrausch in the late 1800s
and such decays are therefore also referred to as Kohlrausch decays.
The recombination dynamics of carriers in LEDs is one of the factors that limits the time it takes to switch an LED on and off. The modulation speed of LEDs used for communication applications can be limited by the minority carrier lifetime. The carrier lifetime can be reduced by either a high doping of the active region or a high concentration of injected carriers in the active region. Heterostructures that confine free carriers to the small well region are frequently employed to obtain high carrier concentrations and thus short carrier lifetimes.

 Опубликовано в
Опубликовано в