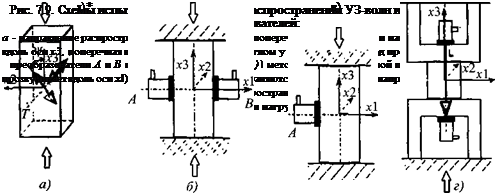
Основы метода. Тензометрия - из­мерение напряжений и деформаций в твердых телах. Акустическая тензометрия основана на явлении акустоупругости, которое заключается в изменении скоро­сти распространения упругих волн под влиянием напряжений. Ниже в возможно более простой форме изложены законо­мерности, поясняющие это явление.

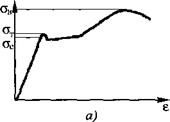
Закон Гука (см. разд. 1.1.1), согласно которому напряжение о и деформация є пропорциональны, выполняется прибли­женно. Более точная зависимость имеет вид

степенного ряда

о = С, е + С2е2 . (7.2)

Степени выше второй не учитывают. Это выражение следует понимать как упро­щенное, не учитывающее наличия и взаи­модействия деформаций разного типа. Коэффициенты типа С і называют упруги­ми постоянными или модулями упругости, а коэффициенты типа С2 (в изотропном твердом теле их три) обычно называют коэффициентами Мурнагана или другими терминами. В [247] вопрос рассматривает­ся упрощенно и показано, что

Дс/с = bC2/Cj «аС2/С .

Таким образом, изменение скорости пропорционально напряжению или де­формации в контролируемом объекте. Связь между ними определяется акусто - упругим коэффициентом. Величина изме­нения скорости Дс/с имеет порядок 10'4, т. е. 0,01 %. Заметим [29], что при дефор­мации растяжения скорость уменьшается, а при деформации сжатия - увеличивает­
ся. В области пластических деформаций скорость остается практически постоян­ной.

Измерение абсолютных значений скорости с необходимой точностью - трудная задача. Она облегчается тем, что обычно требуется измерить не абсолют­ную величину, а изменение скорости под влиянием приложенных напряжении (как и в других вариантах тензометрии). Важ­ное достоинство акустической тензомет­рии - измерение напряжений не только на поверхности, но также внутри ОК. Тща­тельное измерение скорости продольных и поперечных волн в дюралюминии и чугу­не, ее зависимости от одноосного напря­жения выполнено в [183].

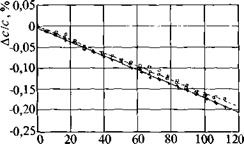
Определение напряжений в материа­лах, обладающих собственной анизотро­пией, требует учета реальной скорости звука в направлении измеряемых напря­жений. Например, текстура, возникающая при прокатке дюралюминия Д16, может вызвать изменение скорости по разным направлениям до 0,26 %, а изменение ско-

а, МПа

Рис. 7.10. Относительные изменения
скорости под влиянием приложенных
напряжений:

□ - измерения непрерывными волнами
методом прохождения; ♦ - импульсные
измерения эхометодом

рости под влиянием напряжений - поряд­ка 0,08 %; для стали 45 соответственно 0,64 % и 0,04 %.

Обнаружено явление динамической акустоупругости [250]. Оно заключается в том, что при воздействии на ОК пере­менного поля напряжений скорость ульт­развука под их воздействием изменяется приблизительно так же, как в стационар­ном режиме. Например, при возбуждении

1

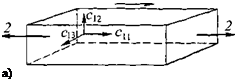
Рис. 7.11. Направления распространения плоских волн (/) и приложенные напряжения (2)

продольных колебаний в образце в виде стержня на частотах 400 ... 600 Гц обна­ружено изменение времени пробега им­пульса продольных волн частотой 5 МГц, направленных перпендикулярно оси стержня. Величина изменения про­порциональна амплитуде переменного напряжения в образце. Явление может быть использовано для контроля перемен­ных напряжений.

В [425, с. 535/647] представлены фак­тические данные о величине акустоупру - гого взаимодействия в зависимости от направления приложенного напряжения (рис. 7.9 и 7.10). В виде таблиц даны по­лезные сведения о величинах акустоупру - гих коэффициентов для продольных, по­перечных и поверхностных волн в некото­рых конструкционных материалах. Экспе­риментальные измерения выполнялись методом прохождения и отражения. Ис­пользовался дефектоскоп EPOCH III и коммерческие преобразователи.

В [425, с. 385/440] развивается теория акустоупругого взаимодействия с лога­рифмической формой представления ко­нечной деформации. Это представление считают перспективным. Изменение ско­рости под влиянием напряжений очень мало, измерениям сильно мешают темпе­ратурные эффекты, микронеоднородно­сти, текстура. Схемы выполнявшихся экс­периментов показаны на рис. 7.11.

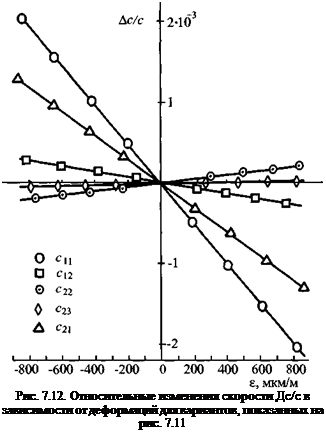
В качестве образцов использовали алюминево-магниевый сплав, технический алюминиевый сплав и оптическое стекло. Для них измерены акустоупругие коэффи­циенты. Измерения выполняли импульс­ным методом с учетом изменения фазы импульса и методом непрерывных воли с наложением модуляции. Точность первого метода была на 10 % выше, результаты показаны на рис. 7.12.

Кроме того, использовали метод двойного лучепреломления поперечных волн, поляризованных под углом 45° к направлению приложенных напряжений. Различия с импульсным методом состав­ляли менее 0,6 %.

В. В. Кошевым и др. [425, с. 103/189; 421, докл. 2.14] предложен способ оценки преддефектного состояния материала и ресурса работоспособности изделия пу­тем определения пространственного рас­пределения параметров напряженно- деформированного состояния. Методика названа авторами томографической.

В работе выделены особенности зон­дируемых сред, относительно которых адекватным алгоритмическим аппаратом определяется пространственное распреде­ление неоднородностей. Показано, что в случае ультразвукового зондирования твердые тела в преддефектном состоянии (при отсутствии сформировавшихся де­фектов) удовлетворяют этим особенно­стям.

Изложена концепция построения то­мографических систем, которая базирует­ся на формировании статистического эта­лона, предварительном выделении ано­мальных областей и (при необходимости) томографическом восстановлении неод­нородностей в заданной аномальной об­ласти.

Представлена ультразвуковая томо­графическая диагностическая система на базе IBM PC/AT, предназначенная для неразрушающего контроля толстолисто­вых (толщиной 20 ... 30 мм) изделий при одностороннем доступе к ним. Диагности­ческая система позволяет восстанавливать пространственное распределение парамет­ров напряженно-деформированного со­стояния материала.

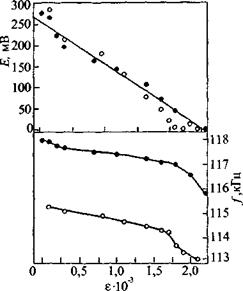
Рис. 7.13. Связь параметров ЭМА-сигнала Е и частоты /с микроискажениями кристаллической решетки є для сталей У8 (•) и ШХ15 (о)

Авторы этой книги считают идею способа интересной, но в представленной работе многое не объясняется. Например, неясен способ контроля скорости по тол­щине ОК, алгоритм обработки информа­ции. Отсутствуют экспериментальные данные, подтверждающие эффективность способа.

В [425, с. 137/429] те же авторы тео­ретически решают задачу реконструкции тензорного поля напряжений в объеме изделия с помощью УЗ компьютерных томографических методов в негомоген­ном материале. Предполагают, что мате­риал прозвучивается продольными и по­перечными волнами в трех направлениях и относительное изменение времени рас­пространения линейно связано с измеряе­мой компонентой тензора напряжений. Предложено два направления решения задачи. Первое связано с измерением ком­понент тензора напряжений с помощью УЗ-томографии, второе - с реконструкци­ей инварианта тензора напряжений.

Перспективно исследование напря­жений по затуханию ультразвука, хотя вопрос этот слабо изучен. Установлено, однако, что повышение напряжений в се­ром чугуне вызывает увеличение затуха­ния рэлеевских волн [50]. При сжатии об­разцов до предела текучести амплитуда сигнала рэлеевской волны, прошедшего через базу 40 мм между излучателем с приемником, увеличивалась в 1,5 ... 2 раза (по сравнению с ненапряженным состоя­нием), а при растяжении - уменьшалась приблизительно в 2 раза. Изменения были более заметны в чугуне с большим содер­жанием пластинчатого графита. Авторы работы объясняют обнаруженное явление тем, что при сжатии графитовые включе­ния плотнее прилегают к металлической матрице, что приводит к большей акусти­ческой прозрачности границы графит - металл. При растяжении происходит об­ратный процесс.

Э. С. Горкуновым и др. [94] примени­тельно к сталям У 8 и ШХ15 установлено, что амплитуда сигнала, возбуждаемого ЭМА-преобразователем, однозначно и практически линейно уменьшается с уве­личением микроискажений кристалличе­ской решетки є, характеризующих микро­напряжения (рис. 7.13). Значение є изме­ряли рентгеноструктурным методом. Уменьшается также резонансная частота колебаний образца, возбуждаемого ЭМА - способом, но в значительно меньшей сте­пени.

Обнаруженный эффект дает возмож­ность использовать ЭМА-преобразование для оценки внутренних напряжений при термической обработке углеродистых и слаболегировынных сталей. Это тем более важно, что эффект проявляется при тем­пературах отпуска 200 ... 600 °С, где маг­нитные и электрические методы контроля неэффективны.

Измерение напряжений в сварных соединениях. Акустический метод позво­ляет исследовать остаточные напряже-

I М' г і

ния; возникающие в соединении в резуль-

тате сварки. В [425, с. 224/785] рассмотрены потенциальные возможности УЗ для изу­чения остаточных напряжений с учетом микроструктуры металла. Образцы из ста­ли S335 имели размеры 300 х 400 мм и толщины 8 и 30 мм. Посередине ширины образцов проходил стыковой шов с раз­делкой кромок. Измерялась скорость го­ловной волны методом прохождения вдоль шва. На частоте 10 МГц измерения

локализовались в слое толщиной 1,5 мм, а на 2,5 МГц - в слое толщиной 2,5 мм. Предварительно измерялся акустоупругий коэффициент путем калибровки (опреде­ления изменения скорости при напряже­нии 400 МПа). Для основного металла он оказался равным (-1,25 + 0,05)10"5 МПа'1, в зоне термического влияния 0,9 от этой величины, а для наплавленного металла 0,8 от этой величины.

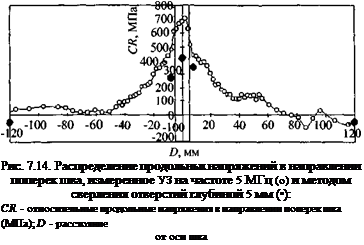
Измерения остаточных напряжений по изменению скорости проводилось на шве и в зоне термического влияния с ша­гом 2 мм, а на основном металле с шагом 5 мм. Результаты удовлетворительно сов­падали с данными, полученными рентге­носпектральным методом и методом свер­ления отверстий (рис. 7.14). Совпадение улучшалось, когда учитывалось влияние на изменение скорости микроструктуры.

Эффективность применения для из­мерения остаточных напряжений в свар­ных соединениях по изменению скорости метода ультразвуковой томографии с усо­вершенствованной компьютерной обра­боткой результатов обосновывается в [425, с. 103/189]. Предложена методика формирования адаптивных проекций, ко­торая позволяет не только обнаруживать дефекты, но также определять ослаблен­ные дефектами участки ОК, обнаруживать нарушения структуры, оценивать напря­жения в металлах и композиционных ма­териалах (рис. 7.15).

Измерения напряжений затяжки резьбовых соединений (болтов и шпилек) - пример эффективного практического при­менения акустической тензометрии. Обычно напряжение затяжки измеряют по приложенной во время затяжки силе к динамометрическому гаечному ключу. Однако это измерение неточно: на резуль­таты сильно влияет такой неизвестный фактор, как величина трения головки бол­та или гайки о поверхность соединяемой детали. Акустический метод свободен от указанного недостатка: он измеряет имен­но напряжение в болте.

Измеряют скорость распространения продольных волн вдоль оси шпильки или болта. Для этого прямой преобразователь прижимают к его торцу или головке и из­меряют время прихода эхосигнала от про­тивоположного торца в процессе затяжки болта. Важно сохранить постоянное по­ложение преобразователя на болте во вре­мя измерений, чтобы не изменялась тол­щина контактного слоя между преобразо­вателем и болтом.

Повышению точности измерения способствует то обстоятельство, что на увеличение времени прихода ультразвука влияют одновременно два фактора: уменьшение скорости и удлинение болта под влиянием прилагаемых напряжений. Наблюдается практически линейная зави­симость времени пробега от напряжения [29].

Для контроля напряжений в резьбо­вых соединениях В. М. Бобренко и

А. С. Рудаковым [30] создан прибор НЗМ 001. Им контролируют детали диаметром 8 мм и более, длиной 20 ... 4500 мм. Огра­ничения связаны с отражением и транс­формацией продольных волн от боковой поверхности (см. разд. 2.2.3.4). В зависи­мости от длины ОК прибор измеряет из­менение времени прохождения импульсов на 0,1 ... 10 мкс под действием затяжки. Это позволяет измерять напряжение за­тяжки 7 МПа и более.

Сравнение способов контроля затяж­ки резьбовых соединений показывает пре­имущества акустического способа, не­смотря на погрешности, связанные с ше­роховатостью или неровностью поверхно­стей ввода и отражающей, влиянием тем­пературы и марки материала соединения.

Тарировка болтов по параметрам на­пряжение - время пробега импульса по­зволяет следить за растяжением каждого болта в стыковочных узлах, содержащих много болтов [30], например фланцевого соединения сосуда с днищем. Это дает возможность установить причину раскры­тия стыка при подаче рабочего давления. Она может, например, заключаться в не­достаточной жесткости фланца.

В [422, с. 1893] исследовали вопрос контроля напряжений в болтовых соеди­нениях электрических генераторов по времени пробега УЗ-импульса. Отмечает­ся, что в длинных (5 ...6 м) болтах время пробега импульса продольных волн суще­ственно больше, чем в безграничном (по диаметру) образце такого же материала. Это связано с отражениями от боковых поверхностей и началом образования волн в стержнях и проявлением геометрической дисперсии скорости (см. разд. 1.4). Это явление не наблюдается, если применять поперечные волны, не подверженные гео­метрической дисперсии скорости.

Время пробега измеряли по фронту первого отрицательного полупериода ко­лебаний импульса, имевшего большую амплитуду. Фиксировали увеличение вре­мени пробега на 0,8 мкс, что соответство­вало удлинению болта на 0,02 %.

В. Т. Власов и Б. Н. Марин [421, докл. 2.72] предложили контролировать затяжку болтов по изменению двух сосед­них резонансных частот. В случае боль­ших усилий затяжки или использования болтов из высокопрочного материала ре­комендован способ контроля, основанный на появлении значительных нелинейных искажений. Они выражаются в том, что в зависимости от напряжений затяжки ам­плитуды колебаний, соответствующих второй и третьей гармоникам, возрастают до величины амплитуды основной гармо­ники. Неясно, однако, как учесть влияние на резонансные частоты соприкосновения болта с соединяемыми деталями.

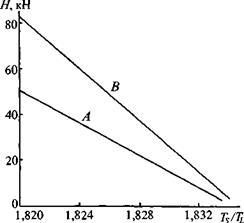
В [425, с. 536/083] рассмотрен вопрос акустоупругого контроля осевой нагрузки болтов. Разработано два способа измере­ний. В первом измеряется увеличение времени пробега АТ импульса в болте под влиянием осевой нагрузки. Во втором из­меряется отношение времен пробега в болте импульсов поперечных и продоль­ных волн TSITL. Этот метод не требует предварительного измерения времени пробега в ненагруженном болте.

На рис. 7.16 представлены калибро­вочные кривые для двух болтов при кон­троле этим способом. Болт В приблизи­тельно вдвое короче болта А. Видно, что измерения дают более высокую точность в случае коротких сильно нагруженных болтов. Предусмотрена цифровая обра­ботка результатов на компьютере. При измерениях необходимо учитывать длину нагруженного участка болта, исключая, например, его головку.

Рис. 7.16. Калибровочные кривые для метода измерений осевой нагрузки в болтах (Н, кН) по отношению времен пробега поперечных и продольных волн (TSITL)

Контроль напряжений в ободах железнодорожных колес. Методика раз­работана в Италии [422, с. 1964] и Герма­нии [422, с. 1972]. Измеряемый параметр - время пробега УЗ-импульса по толщине обода колеса (рис. 7.17). Цифры на рисун­ке указывают значения тангенциальных (перпендикулярных плоскости рисунка) напряжений в МПа, измеренных не УЗ - способом: а - напряжения при торможе­нии (наиболее опасный момент), б - при движении состава.

Необходимо контролировать именно тангенциальную составляющую напряже­ний а, ап, в то время как радиальная состав­ляющая С rad остается практически посто­янной. С учетом этого применяют попе­речные волны, поляризованные в танген­циальном и радиальном направлениях, скорость которых либо изменяется, либо практически не изменяется под действием соответствующих напряжений. Измеряют относительное изменение времени t про­бега. Используют уравнение

*^tan ~ ^rad — ^(бап ~ ^rad )/бап >

где К - коэффициент пропорционально­сти, определяемый в лабораторных усло­виях для контролируемого материала. Из-

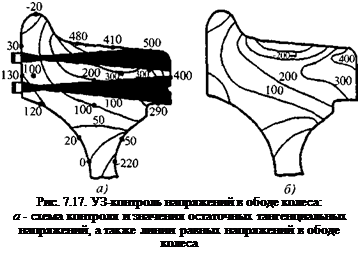мерения выполняют по окружности коле­са, а распределение напряжений по глуби­не определяют при радиальном смещении преобразователя.

Измерениям мешает текстурирован- ность материала колеса. О степени тексту - рированности можно судить по амплитуде эхосигнала в зависимости от поворота плоскости поляризации. В текстурирован­ном материале амплитуда сильно изменя­ется. Колеса из текстурированного мате­риала контролировать можно, если тек­стура сохраняется постоянной, но точ­ность измерений снижается на ± 20 МПа.

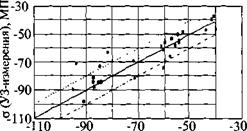
О (измерения электросопротивлением), МПа Рис. 7.18. Сопоставление остаточных напряжений для трех новых колес, измеренных УЗ-методом н методом электросопротивлений для ободов колес диаметрами: • - 850; ■ - 920; - 1250 мм

Для контроля напряжений в ободах колес в Италии разработана система ЕСОМАТ, а в Германии - система USER. На рис. 7.18 показано сопоставление ре­зультатов измерения напряжений датчи­ком электросопротивлений (на оси абс­цисс) и системой ЕСОМАТ. Погрешность измерений - 10 МПа. Время контроля од­ного колеса 1,5 мин.

Контроль натяжения канатов и стержней. Акустические методы приме­няют для контроля натяжения стержневой или проволочной арматуры при изготов­лении предварительно напряженных же­лезобетонных конструкций. Используют зависимость частоты поперечных свобод­ных колебаний арматуры от силы ее натя­жения [87]. Известно, что для струны, из - гибная жесткость которой пренебрежимо мала, упругость определяется только на­тяжением а, которое связано с основной собственной частотой / поперечных коле­баний соотношением

а = 4р/2/2,

где р - плотность материала струны, / - ее длина.

Однако, в отличие от струны, стер­жень обладает изгибной жесткостью, что необходимо учитывать. В данном случае натяжение стержня (подобного струне) вызывает не изменение скорости распро-

странения в нем звука, а затрудняет из - гибную деформацию его элементов, т. е. изменяет условия колебаний.

В работе [87] получена уточненная формула, учитывающая реальную изгиб - ную жесткость арматуры. Для стальных стержней она имеет вид

— -1,25 —

УТ I

Здесь напряжение а в МПа; Т - пери­од основного тона колебаний арматуры, мс; I - свободная длина арматуры, см; d - номинальный диаметр арматуры, мм. Экс­периментальная проверка показала, что погрешность расчетов по этой формуле не превышает ± 1 %, а общая погрешность для всех видов арматуры при ее свободной длине 3 м и более не превышает допусти­мого значения (± 4 %) по ГОСТ 22362.

Разработанный прибор ГСП АП-12 измеряет частоту поперечных колебаний, возбуждаемых приложением и резким сбросом небольшого усилия на середине свободной длины арматуры. Пьезоэлек­трический приемник с биморфным пьезо­элементом крепят на ОК с помощью маг­нитов. Измеряемая частота лежит в диапа­зоне 2 ... 200 Гц, что ниже собственной частоты приемника.

Определяли напряжения от 100 до 1400 МПа в арматуре из стальных стерж­ней. Для повышения точности измерений отбрасывали первые 4 периода и измере­ние среднего значения периода колебаний вели по последующим четырем периодам.