Вентилирование помещений любого назначения представляет со­бой процесс переноса определенных объемов воздуха, вытекающего из приточных отверстий. Скорость и направление истечения воздуха из отверстий, форма и количество отверстий, их расположение, а также температура воздуха в струе определяют характер воздушных потоков в помещении. Приточные струи взаимодействуют между собой, с тепло­выми струями, возникающими около нагретых поверхностей, и с пото­ками воздуха, образующимися вблизи вытяжных отверстий.

Строительные конструкции помещения (колонны, стены, пол, по­толок) и технологическое оборудование при набегании на них потоков воздуха оказывают существенное влияние на скорость и направление их дальнейшего распространения. Кроме того, в производственных по­мещениях на скорость и направление движения воздуха большое влия­ние могут оказывать действие различных механизмов технологического оборудования, а также струи, истекающие из отверстий или неплотно­стей оборудования, находящегося под избыточным давлением.

Воздушные потоки — струи, образующиеся в помещении, — пере­носят поступающие в воздух вредные выделения (конвективное тепло, пары, газы и пыль) и формируют в объеме воздуха помещения поля скоростей, температур и концентраций. «В распространении вреднос­тей по помещению струям, иначе говоря, турбулентной диффузии (в противоположность молекулярной диффузии) принадлежит решаю­щая роль» [7].

При распределении приточного воздуха в вентилируемом помеще­нии необходимо учитывать все особенности распространения приточ­ных струй, с тем чтобы в рабочей или обслуживаемой зоне помещения обеспечить требуемые параметры воздуха: температуру, подвижность и допустимые концентрации вредных выделений (включая влажность). Учет всех особенностей движения воздуха в помещении представляет собой задачу большой сложности, так как не все факторы, обусловли­вающие это движение, поддаются точному учету — к настоящему вре­мени некоторые из них еще недостаточно изучены.

Систематическое изучение струй началось около 60 лет назад и продолжается до настоящего времени. Столь большой интерес к струям объясняется применимостью их в различных областях техники.

Струей называют поток жидкости или газа с конечными попереч­ными размерами.

В технике вентиляции приходится иметь дело со струями воздуха, истекающего в помещение, также заполненное воздухом. Такие струи называют затопленными.

В зависимости от гидродинамического режима струи могут быть ламинарными и турбулентными. Приточные вентиляционные струи всегда турбулентны.

Различают струи изотермические и неизотермические. Струю на­зывают изотермической, если температура во всем объеме ее одинако­ва и равна температуре окружающего воздуха. Для вентилирования помещений в подавляющем большинстве случаев применяются неизо­термические струи.

Струю называют свободной, если она истекает в достаточно боль­шое пространство и не имеет никаких помех для своего свободного раз­вития. Если на развитие струи ограждающие конструкции помещения оказывают какое-либо воздействие, то такую струю называют несво­бодной, или стесненной. Вентиляционные приточные струи развиваются в помещениях ограниченных размеров и могут испытывать влияние ог­раждающих конструкций. При определенных условиях влияние ограж­дений на развитие приточных струй можно не учитывать и считать такие струи свободными.

Струя, истекающая из отверстия, расположенного вблизи какой - либо плоскости ограждения помещения (например, потолка), парал­лельно этой плоскости, будет настилаться на нее. Такую струю называ­ют нйстилающейся.

Все приточные струи можно разделить на две группы: 1—с па­раллельными векторами скоростей истечения; 2 — с векторами скоро­стей истечения, составляющими между собой некоторый угол.

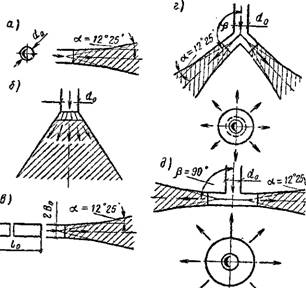
Геометрическая форма приточного насадка определяет форму и закономерности развития истекающей из него струи. По форме разли­чают струи компактные, плоские и кольцевые (рис. IX.1).

Компактные струи образуются при истечении воздуха из круглых, квадратных и прямоугольных отверстий. Струя, истекающая из круг­лого отверстия, остается осесимметричной по всей длине своего разви­тия (круглая струя). При истечении из квадратного или прямоугольно­го отверстия струя в начале не будет осесимметричной, но на некото­ром расстоянии от насадка преобразуется в осесимметричную. При истечении воздуха из круглого отверстия с диффузорами для принуди­тельного расширения образуется также компактная струя, которая будет осесимметрична по всей длине; такую струю называют кониче­ской.

Плоские струи образуются при истечении воздуха из щелевых от­верстий бесконечной длины. В реальных условиях плоской считают струю, истекающую из длинного щелевидного насадка с соотношением сторон /о:2£о^20. Струя, истекающая из щели с соизмеримым соот­ношением сторон, не остается плоской, а постепенно трансформируется сначала в эллипсовидную и на расстоянии x—§dycn в круглую (за <іУсл принимают корень квадратный из площади щели).

Если струя истекает из кольцевой щели под углом к оси подводя­щего воздух канала р<180°, то ее называют кольцевой, при р около 135° — полой конической, при р=90° — полной веерной. У полных веер­ных струй угол распределения воздуха в пространство составляет 360°; при меньшем угле распределения струя будет неполной веерной.

При угле (3 « 160° и большем может образовываться компактная струя.

Независимо от формы все струи, у которых при истечении нет при­нудительного изменения их направления, на некотором расстоянии от насадка расширяются; угол бокового расширения а=12°25'. Угол рас-

Рис. IX. 1. Струи различной формы С — компактная осесимметричная; б —» коническая; в — плоская; г — кольцевая (полая коническая); д — полная веерная

Ширения конической струи при истечении почти совпадает с углом на­правляющих диффузоров, а затем постепенно уменьшается и на рас­стоянии 10 d0 становится равным углу естественного бокового расшире­ния (12°25').

Изучение струй проводилось многими отечественными и зарубеж­ными исследователями применительно к различным областям техники. Наиболее глубокое и полное исследование струй принадлежит Г. Н. Абрамовичу [2]. Применительно к задачам вентиляционной тех­ники широкие исследования струй проведены И. А. Шепелевым [58].

§ 39. СВОБОДНЫЕ ИЗОТЕРМИЧЕСКИЕ СТРУИ

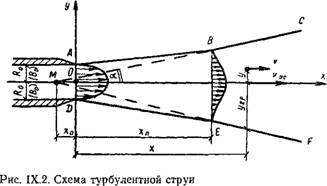
Упрощенная схема свободной турбулентной изотермической струи представлена на рис. IX.2. Воздух, вытекая из отверстия, образует струю с криволинейными границами ABC и DEF, которые приближен­но могут быть заменены прямыми АВ, ВС, DE и EF.

В струе различают два участка: начальный ABED и основной CBEF. Сечение BE называют переходным сечением. В начальном уча­стке струи поле скоростей истечения (начальное поле) формируется в поле скоростей основного участка. В общем случае начальное поле скоростей может быть равномерным или неравномерным. При равно­мерном поле скоростей в пределах начального участка на оси струи и во всех точках некоторого объема ее сохраняются начальные парамет­ры истечения: скорость, температура и концентрация (в круглой струе — это объем конуса, основание которого совпадает с плоскостью истече­ния, а высота равна длине начального участка).

Границы основного участка струи ВС и EF при их продолжении пересекаются в точке М, называемой полюсом струи. Положение полю­са точно не установлено. Известно только, что при равномерном на­

Чальном поле скоростей точка М находится примерно в центре выход­ного отверстия.

В основном участке струи скорость воздуха на оси потока и в пе­риферийной части по мере удаления от выходного отверстия непрерыв­но уменьшается. Профили скоростей воздуха в различных поперечных сечениях основного участка струи подобны и описываются одними и теми же безразмерными зависимостями.

Турбулентная струя, как и всякое турбулентное течение, характе­ризуется интенсивным поперечным перемещением частиц. Частицы воз­духа, совершая кроме поступательного движения вдоль потока по­перечные перемещения в составе вихревых масс, вовлекают в поток частицы окружающего воздуха, которые тормозят периферийные слои струи. В результате масса струи растет, площадь ее поперечного сече­ния увеличивается, а скорость уменьшается.

Перенос - вихревых масс, обусловливающий изменение скоростей в струе, обусловливает также распределение в струе концентраций и тем­ператур (для неизотермических струй).

По внешнему периметру струи из заторможенных частиц потока и из частиц воздуха, вовлеченных в поток, образуется пограничный слой.

В теории свободных струй исходным положением для выявления закономерностей их развития является равенство статических давле­ний в струе и окружающем воздухе. Вследствие этого положения им­пульс внешних сил будет равен нулю, а количество движения секунд­ной массы воздуха в струе должно быть постоянным:

/0 = 7, = const. (IX. 1)

В настоящее время имеются исследования, оспаривающие положение о равенстве статических давлений в струе и в окружающем воздухе и, следовательно, о постоянстве количества движения в струе. К числу таких работ относятся исследования В. А. Бахаре - ва [9] и ряд экспериментальных работ других авторов. В этих работах показано, что статическое давление в струе изменяется и вдоль оси и от оси к границе. В отличие от существующих оценок свободной струи как системы незамкнутой В. А. Бахарев предла­гает рассматривать ее как систему замкнутую, т. е. вместе с частью окружающего про-

О 0,2 0,4 0,6 0,8 Ю V

И=0

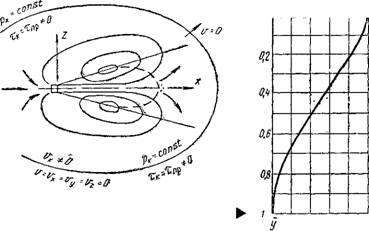
Рис. IX 3. Свободная струя внутри замкнутой системы Рис. IX.4. Поле скоростей в поперечном сечении струи

Странства, очерченной некоторым контуром, на котором нет обмена энергией с другими системами. Обратные потсуси воздуха, возникающие около свободной струи, в этом слу­чае будут находиться в пределах этого контура (рис. IX.3).

Ниже приводятся данные о струях по теории Г. Н. Абрамовича в обработке В. Н. Талиева [48].

Рассматриваются круглая, плоская и кольцевая струи.

Для всех трех форм струи поле скоростей в основном участке при­нимается по аналитической зависимости Г. Шлихтинга:

У = (IX.2)

Где v = v/v0с — относительная скорость воздуха в рассматриваемой точке попе­речного сечения струи — отношение скорости в точке к скорости на оси струи; у — — у/Утр — относительная ордината рассматриваемой точки в поперечном сечении струи — отношение ординаты точки к ординате границы струи (к полуширине струи).

Зависимость (IX.2) фиксирует скорость на границе струи:

Л У 1 v = 0 при------------------------------------------- = 1.

Угр

Графическое изображение зависимости (IX.2) приводится на рис. IX.4. Экспериментальные исследования, проведенные различными авторами, показывают, что зависимость (IX.2) хорошо описывает рас­пределение скоростей в поперечном сечении струи*.

Круглая свободная изотермическая струя. Из круглого отверстия радиусом Rq вытекает воздух, образуя струю круглого поперечного се­чения (см. рис. IX.2). Поле скоростей в отверстии неравномерно. Сред­няя по площади отверстия скорость равна v0. Начало координат поме­стим в центре отверстия, а ось абсцисс х направим по оси струи.

Относительный радиус струи

~Rx = — tg а = (я — хо) tg а, (IX.3)

Но

Где x=x/R0 — относительное расстояние; x0 = xJR0 — относительная абсцисса по­люса основного участка струи.

Исходя из постоянства количества движения секундной массы воз­духа в струе, будём иметь:

PpVf=P0PVO» (іх-4)

Где £ и — поправочные коэффициенты на количество движения в сечениях на расстоянии х от отверстия и на выходе из него; р — плотность воздуха в струе; Ьх и Lo — объемный расход воздуха соответственно в рассматриваемом сечении и на выходе из отверстия; vF и v0 — средняя по площади скорость движения воздуха в тех же се­чениях.

Равенство (IX.4) представляет собой уравнение количества движе­ния в проекциях на ось струи. В нем не учитывается количество движе­ния окружающего воздуха, питающего струю, а также угол бокового расширения струи, т. е. принято, что скорость и ее проекция равны (cos 12°25'=0,98«1).

Заменяя Lx и L0 через vPFx и v0F0, а площади Fx и F0 через iiRl и jt/?o, получим относительную среднюю по площади скорость:

VFo

—==—----------------------------------------------------------------- . (IX.5)

0 V^Cx-ч) tg a

Относительная средняя по расходу скорость[4]

L

F ФdL

VM о 1

«о pLx "о

« где vM — средняя по расходу скорость; v — скорость в любой точке поперечного сечения струи; dL — элементарный объемный расход воздуха в струе.

Так как количество движения во всех сечениях струи остается по­стоянным и равным количеству движения в начале струи, то

- _ РоРІоРо _ М^О Ро Vh V'p ' м pLxvо nR2xvF00 Rl VF (х — х0) tg а

Относительная осевая скорость

- _ Оос VF 1 1 - V0c--------------- = — ----- — =

(IX.6)

Щ К v0 к

(IX. 7)

Уїо

KV$ (X — хо) tg а

Где t'oc — скорость на оси струи (осевая скорость) в сечении, находящемся на расстоянии х от начала истечения; К — коэффициент поля скоростей для того же сече­ния; K=vF/v ос.

Относительный объемный расход

_ Lx nRlvp Lx = -7і = —— = Rtv -

Х UF

Л/?о Oq

(x — xo) tgo. (IX.8)

Гї

Jo

Vt

Коэффициент поля скоростей К можно определить, имея в виду, что

Lx HvdF

Тогда

Fx °ос

D (яг2) 2nrdr - _

DF = * =----------------------------------------- — =2 rdr.

NR* nR

Используя зависимость (IX.2), вычисляем коэффициент поля ско­ростей:

К = 2 J(l — ?'5 f~rd~r = 0,258.

О

Поправочный коэффициент на количество движения |3, называемый коэффициентом Буссинеска, может быть записан в следующем виде:

Используя зависимость (IX.2) и dF=2rdr, получим: 2 Г/, -1.5Ч4-- °>134

Г(і — ?*yrdr= — 2,02.

Я2 J 0,258а

Подставляя полученные значения коэффициентов К и р в формулы. (ІХ.5) — (ІХ.8) и учитывая, что tg 12с25'=0,22, получаем расчетные формулы для круглой струи (табл. IX.1). В таблице приведены также расчетные зависимости для избыточных концентраций и для кинетиче­ской энергии, вывод которых не приводится.

(IX. 9)

По формулам табл. IX.1 могут рассчитываться и-струи, вытекаю­щие из прямоугольных отверстий с соизмеримыми размерами сторон. При этом в формулах вместо Ro следует использовать

Яэкв = у^F0 = 0,565 Vf0 .

В этом случае относительные величины, входящие в расчетные фор­мулы, определяют через Яэкв. Например,

TOC o "1-3" h z х -"-On

Хо — ~ > %

D і лі) D О

Аэкв Аэкв Аэкв

Поправочный коэффициент на количество движения секундной массы воздуха в начале истечения р0 может быть вычислен при усло­вии, что известно начальное поле скоростей. В случае равномерного поля скоростей Ро=Ь

Для определения Ро может быть использовано предложение В. В. Батурина о примерном равенстве коэффициента местного сопро­тивления насадка £ и поправочного коэффициента на скоростное давле­ние а, т. е. azzt,. Тогда Ро« (£+2)/3. _

Относительная абсцисса полюса основного участка струи х0 мо­жет быть определена из формулы (г) табл. IX. 1, если из эксперимен­тов с данной струей известны величины у ос» Vq и ро.

Таблица IX.1

Расчетные формулы для круглой струи

Расчетная формула

Расчетная величина

Обозначение величины

Относительный радиус струи

Относительная средняя по площади скорость. .

Относительная средняя по расходу скорость. .

Относительная осевая скорость

Относительный объем­ный расход

Относительная средняя по расходу избыточная концентрация

Относительная кинети­ческая энергия....

«г-5* Ro

Уо иМ Оо Рос fo

Им Foe

Х L*

Окр

АС

М

С о Со = §х Ео С ОС ~~~ Сріф Cq С0Кр

'Окр

АСо

Относительная избы­точная концентрация на оси струи

0,22(х—х0) 3,2 VT*

X xq

6,45 V 12,4 VS"

X — Xq

(е) (ж) (з)

0,155 УПЙ" (х — ж0) (д) 6,45

Кро (х — х0) 6,42 УТ0 (ЗР0-2) (х~хй) 9,24

<*) (б) (в) (г)

О (х—ха)

При равномерном начальном поле скоростей относительное полюс­ное расстояние т. е. в этом случае полюс основного участка струи находится в плоскости начала истечения.

Основываясь на экспериментальных данных, можно с некоторым приближением принимать следующие значения относительного полюс­ного расстояния:

Р.. • <1,04 1,04—1,1 1,1—1,2

0 0—(-4) (—4)—(—5,2)

И

Длину начального участка хи можно определить из формулы (г)

Табл. IX. 1, приняв оос = »о; при равномерном поле скоростей р0 х0«Ои хи—12,4 Rq.

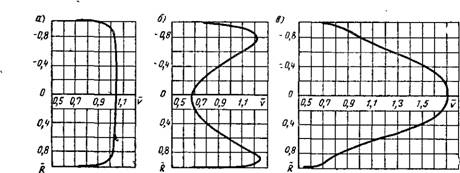
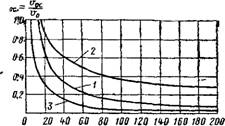
На рис. IX.5 представлены результаты проведенных В. Н. Талиевым и А. М. Терпи - няном экспериментальных исследований по распределению скоростей на оси осесиммет­ричной струи для трех случаев истечения воздуха: / — равномерное поле скоростей (/(= =0,966^1; р0 = 1,02); 2 — вогнутое поле скоростей (/(=1,475; р0=1,085); 3 — вы­пуклое поле скоростей (/(=0,588; р0=1,2).

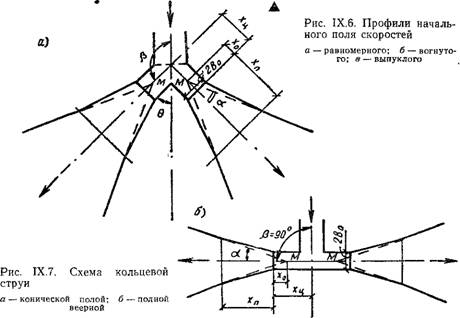
Профили соответствующих начальных пблей скоростей показаны на рис. IX.6.

Из рисунков следует, что неравномерность начального поля скоростей и форма поля оказывают существенное влияние на формирование струи. Длина начального участка при неравномерном поле короче, чем при равномерном. При значениях х^20 все три кри­вые почти эквидистантны, причем кривая /, соответствующая равномерному полю скоро­стей, располагается несколько выше кривых 2 и 3, хотя количество движения для этой струи меньше, чем для случаев 2 и 3 (см. рис. IX.5).

Экспериментальная проверка осевых скоростей, проведенная В. Н. Талиевым и А. М. Терпиняном, показала, что результаты, полученные по формулам Г. Н. Абрамови­ча, хорошо согласуются с опытными данными. Наибольшее отклонение от опыта состав­ляло от +5,5 до —5,9%- Проверка показала также, что пренебрегать полюсным расстоя­нием нельзя, так как это приводит к значительной ошибке.

Рис. IX.5. Относительные скорости вдоль оси осе - симметричной струи

1 — равномерное поле, количество движения /і; 2 — вог­нутое поле, /г=1,085 Л; 3 — выпуклое поле, /з=1,2у

Плоская свободная изотермическая струя. В плоской струе так же, как и в круглой, различают полюсное расстояние х0, начальный участок хп и основной уча­сток (см. рис. IX.2).

Понятие полюса плоской струи ус­ловно; обычно полюс представляет собой точку; в данном же случае это прямая линия, образованная пересече­нием граничных плоскостей основного участка струи.

Таблица IX.2

Расчетные формулы для плоской струи

Расчетная формула

Расчетная величина

Обозначение величины

Относительная полу­ширина струи. . . .

Относительная средняя по площади скорость. .

Относительная средняя по расходу скорость. .

Относительная осевая скорость

Относительный объем­ный расход

Относительная средняя по расходу избыточная концентрация

Относительная кинети­ческая энергия....

Вх_ Во VF VM _ VQC_ Щ

JM

1 См —

Окр

АС

М

Относительная избы­точная концентрация на оси струи......

0

Расчетные зависимости для плоской струи (табл. IX.2) выводятся из тех же условий, что и для круглой, но с учетом особенностей ее гео­метрии.

При равномерном начальном поле скоростей, когда ро=1, полюс струи находится в плоскости начала истечения, т. е. хжО, при неравно­мерном — внутри щели.

Длина начального участка хп определяется из формулы табл. IX.2. При равномерном поле скоростей р0= 1 и хп=14,4 Во.

Кольцевая свободная изотермическая струя (рис. IX.7). Расчетные формулы для кольцевой струи приведены в табл. IX.3.

Если основываться на формуле (г) табл. IX.3 и принять, что в кон­це начального участка а0с=%, то длина начального участка будет за-

Р«с. 1Х*8. Изменение относительной скоро­сти на оси струи при {Зо = 1 и дго=0

1—-круглая струя; 2 —плоская струя_при длине щели I оо; 3 — кольцевая струя при х —2

Таблица IX.3

Расчетные формулы для кольцевой струи

Расчетная формула

Расчетная величина

Обозначение величины

Относительная полу­ширина струи. . . .

Им

VM =■

Lx

Относительная средняя по площади скорость. .

Относительная средняя по расходу скорость. .

Относительная осевая скорость.......

Относительный объем­ный расход

Вх_ Ва Vp_ Щ

Вх =

Относительная средняя по расходу избыточная концентрация

Висеть от величины хц. При Хц=2 и равномерном поле скоростей в на­чале струи д:п»4,5.

Частным случаем кольцевой струи является веерная, у которой выход воздуха из кольцевой щели происходит перпендикулярно оси симметрии (0=90°). Формулы, приведенные в табл. IX.3, справедливы и для веерной струи.

Расчетные формулы для кольцевой струи переходят в формулы ДЛЯ ПЛОСКОЙ струи, если принять в НИХ Хц—ОО.

На рис. IX.8 приведены кривые изменения относительных скорос­тей воздуха на оси круглой струи, плоской струи, истекающей из щеле - видного насадка бесконечной длины, и кольцевой струи при хц=2. Кривые построены по формулам (г) табл. IX. I—IX.3 при равномерных начальных полях скоростей воздуха во всех трех струях.

Наиболее быстрое «затухание» наблюдается у кольцевой струи. Наибольшей дальнобойностью обладает плоская струя.