To obtain high light-extraction efficiency and avoid absorption of light, all semiconductor layers

other than the active region should have a bandgap energy larger than the photon energy. This

can be done in different ways, for example by using double heterostructures, window layers, and other structures that will be discussed below. In this section, we discuss the absorption of light if the energy of the light is below the energy gap of the semiconductor.

Naively, one would assume that a semiconductor can absorb light only if the photon energy is higher than the bandgap energy and that the semiconductor is transparent for photon energies
below the bandgap. However, semiconductors do absorb below-bandgap light, although with a much lower absorption coefficient.

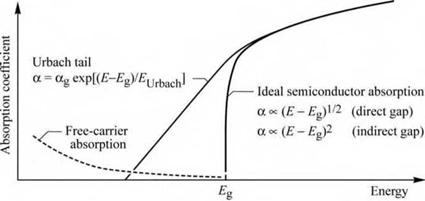
Fig. 9.1. Absorption coeffi­cient of a semiconductor with bandgap Eg versus en­ergy. The “Urbach tail” dominates absorption near but below the bandgap. Ab­sorption further below the bandgap is dominated by free-carrier absorption.

The absorption coefficient versus energy of an idealized semiconductor and a real semiconductor is shown schematically in Fig. 9.1. In the idealized semiconductor at low temperatures, the absorption coefficient versus energy is given by (Pankove, 1971)

а к (E - Eg)1/2 (direct gap) (9.2a)

а к (E - Eg)2 (indirect gap) . (9.2b)

The idealized semiconductor has a zero band-to-band absorption coefficient at the bandgap energy (E = Eg). The absorption strength in a real semiconductor, for below-bandgap light, can be expressed in terms of an exponentially decaying absorption strength. In this absorption tail, called the Urbach tail, the absorption coefficient versus energy is given by

а = agexp[ (E - Eg)/EUrbach] (93)

where аg is the experimentally determined absorption coefficient at the bandgap energy and EUrbach is the characteristic energy (here called the Urbach energy), which determines how rapidly the absorption coefficient decreases for below-bandgap energies.

Urbach (1953) measured the absorption tail for different temperatures and showed that the Urbach energy is approximately kT, the thermal energy. The temperature dependence of the Urbach tail led Knox (1963) to the conclusion that the below-bandgap transitions are phonon - assisted transitions. Thus, the Urbach energy is given by

EUrbach = kT.

The Urbach tail can be caused by mechanisms other than phonon-assisted absorption. Any

mechanism introducing a potential fluctuation will lead to local variations of the semiconductor band edges. As a result of these fluctuations, the bandgap energy fluctuates as well, and below - bandgap transitions can occur.

The most common potential fluctuations are fluctuations caused by random dopant distribution and local variations of the chemical composition of a ternary or quaternary alloy semiconductor.

Potential fluctuations caused by random dopant distribution can be calculated using Poisson statistics. The magnitude of these fluctuations is given by (see, for example, Schubert et al.,

1997)

(9.5)

where rs is the screening radius.

Potential fluctuations caused by random compositional fluctuations can be calculated using binomial statistics. The magnitude of these fluctuations is given by (see, for example, Schubert et al, 1984)
electrons must undergo a momentum change when excited higher within a parabolic band. This momentum change is provided by acoustic phonons, optical phonons, or by impurity scattering.

Free-carrier absorption is proportional to the free-carrier concentration, since a free carrier is required for an absorption event. Theoretical considerations in terms of the classical Drude free - electron model further show that free-carrier absorption increases as the square of the incident wavelength (Pankove, 1971). Thus the proportionalities

22 afc к n X and afc к p X (9.7)

are valid for n-type and p-type semiconductors, respectively. Theoretical considerations in terms of a quantum mechanical treatment show that the absorption coefficient is proportional to X32, X52, and X72 depending upon whether acoustic phonon scattering, optical phonon scattering, or ionized impurity scattering is involved in the momentum conservation process, respectively (Swaminathan and Macrander, 1991).

In n-type and p-type GaAs, the room-temperature free-carrier absorption coefficient near the bandgap energy (X « 950 nm) can be expressed as (Casey and Panish, 1978)

afc = 3 cm_1 —78^---------------- r-- + 7 cm_1 —— . (9 8)

1018 cm-3 1018 cm-3

Inspection of the equation indicates that the free-carrier absorption coefficient can be of the order of 10 cm-1 at high carrier concentrations. Approximate values for the free-carrier absorption coefficient in several compound semiconductors are given in Table 9.1.

In LEDs, free-carrier absorption can affect the intensity of waveguided modes radiating out of the side of the chip. Free-carrier absorption also plays a role in LEDs with transparent

semiconductor substrates. Such transparent substrates have a typical thickness greater than 100 ^m. If the doping concentration of a transparent substrate is high, free-carrier absorption will reduce the light-output power. If it is low, the substrate becomes resistive. Thus a compromise needs to be made between the different doping requirements of a transparent substrate. For thin layers, such as confinement layers, free-carrier absorption effects are negligibly small if the optical path length within the layer is short.