Уравнение движения (импульса). Возьмем не­который элемент движущегося потока йУ=(1х ёу йг (рис. 1.1). На выделенный элемент действуют массовые (объемные) и по­верхностные силы. К массовым силам относится сила тяжести, к поверхностным — силы давления и трения. Рассмотрим слу­чай одномерного течения.

Предположим, что элемент потока (IV движется ВДОЛЬ ОСИ X. Пусть силы удельного давления изменяются только по направле­нию течения потока, т. е. Р = /(*). Тогда в любой точке функцию Р (х) можно разложить в ряд Тейлора. Примем, что на верхней грани удельное давление жидкости равно Р, тогда на площадку с1ус1г действует сила Рс1уйг. На нижней грани (с точностью до второго члена разложения в ряд Тейлора) удельное давление ОР

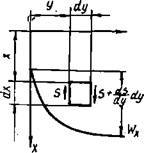Равно Р---^<Ьс, а сила, действующая на эту грань, соответ.

Рис. 1.1. К выводу дифференциального уравнения движения (импульса)

Ствует — [Р -{-^йх^ёуйг. Знак минус указывает на то, что сила

Действует против направления движения. Равнодействующая сил давления на элемент

При движении реальной жидкости всегда возникает сила трения. Поскольку мы рассматриваем движение только вдоль оси X, скорость вязкого потока изменяется только в направле­нии оси У, а силы трения возникают на боковых гранях эле­мента жидкости. Около левой грани скорость движения частиц меньше, чем в самом элементе, поэтому Здесь в сечении У сила трения направлена против движения и равна —5с1хс1г. Около правой грани скорость частиц больше, чем в самом элементе, и в сечении у+йу сила трения направлена в сторону движе­ния. Равнодействующая этих сил равна их алгебраической сумме:

^ йхйг — Бёхйг =

Подставляя 5 = р ^ с учетом закона Ньютона, получаем

' йу*

Если принять, что направление оси X в потоке жидкости сов­падает с направлением действия гравитационных сил (силы тя­

Жести), то силу тяжести, приложенную к элементу объема и действующую в направлении оси X, определим из уравнения

АН =

Согласно основному принципу динамики сумма проекции сил, действующих на движущийся элемент. объема жидкости, равна

^И)х

Произведению массы элемента на его ускорение Следовательно, Ле>х 4р

Р^-==Р2-57+(а-^5--

Описаиие движения усложняется, если скорость'потока из­меняется по трем направлениям. В йбщем случае трехмерного течения поле скоростей вязкой несжимаемой жидкости описы­вается уравнением Навье — Стокса [49]:

Йш, вР / <?2®г д2(иг

Лту дР, , ^у, д\ п п

&>г дР, (&и>г, д2и>г ЛЛ

-№-д2+ *[-&?+ -& + -&}

В случае движения сжимаемой жидкости уравнения Навье—Стокса приобретут вид [1041

TOC o "1-5" h z Лях дР I 1

= 57 + + у <Иуи>];

Р^ь^рЛ“ % +1*(уЧ + - дт(1*у“'): С1-2)

<Ь®г дР I 1

Р~й7 = Р^г~а7 + 1*^*«»» + - д сЛуш].

При движении идеальной жидкости, когда силы трения от­сутствуют, решение уравнений (1.1) для установившегося одно­мерного течения приводит к уравнению Бернулли:

Р + сопэ( (1.3)

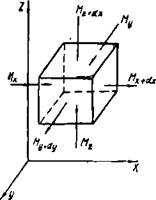
Уравнение сплошности. Выделим в потоке элементарный объем, ориентированный параллельно координатным осям

(рис. 1.2). Подсчитаем массу жидкости, протекающей через него в направлении координатных осей X, У, 1 за время йх.

Пусть составляющая скорости потока вдоль оси X в точках, лежащих на нижней грани параллелепипеда, равна wx. Тогда массу жидкости, входящей в параллелепипед вдоль оси X за время dt, находим из уравнения М* = рWxdydzdz. Через верхнюю грань за то же время dz выйдет масса

Mx+dx = [pQьx d*j dydzd-z.

Приращение массы в объеме dV вдоль оси X будет dM, = М,-Mx+dt = - dxdydzdx.

Рис. 1.2. К выводу дифференциально - Рис. 1.3. К выводу дифференциально­го уравнения сплошности го уравнения энергии

Аналогично запишем приращение массы в объеме параллелепипеда, по координатным осям У,

D^[y —----- dxdydzd■c•f

DfЛг =------ dxdydzd■z.

Общее приращение массы

[д (?т д (ри)А д(Р№,)'

Т--[-г + - тг +

Изменение массы в полностью заполненном объеме возможно только при изменении плотности, поэтому

ЙМ = ^^ЫусШх.

TOC o "1-5" h z Приравнивая выражение для dM, после преобразований получаем аР а (Ряд в(рю) в(р»,) п

* + ^Г + "15- + -*- = °- О-4)

Выполнив операцию дифференцирования, выражение (1.4) пред­ставим как

1 fa dw дш dw,

H + s + iI + t;-0- М

Таким образом получены дифференциальные уравнения (1.4), (1.5) неразрывности потока для неустановившегося течения сжимаемой жидкости.

Для несжимаемой жидкости, когда р = const, уравнение сплош­ности принимает вид

Dm, dw„ dw,

Fc+V+fc"0- №

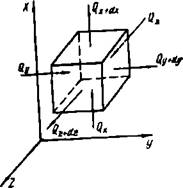
Уравнение переноса энергии (тепла). Выделим в потоке жид­кости элемент объемом dV = dxdydz(рис. 1.3). Пусть составляющая скорости на нижней грани в направлении оси X равна wx. Находим количество тепла, внесенное в объем через грань за время dv, 1

Qx = pWtCjdydzdx,

Где р — плотность; ср — теплоемкость. Величина cppwj представ­ляет собой количество тепла, протекающее в единицу времени через поперечное сечение.

Определим количество тепла, вышедшее через противоположную грань в направлении координаты х:

Гд(с„рat t) "|

Qx+dz = Р WtCptdydzdz + [—^—’-dx^dydzdx =

Г д (с„ри>г) лЛ

= cppwjdydzdz + у ■ дх~ + cppwj; ^ jdxdydzdz.

Отсюда находим приращение количества тепла в элементе объема вследствие конвективного переноса вдоль оси X:

DQr = Qx — Qx+dx = — ["* — + cDpwr dxdydzdt.

Аналогично определяются приращения количества тепла относи­тельно координатных осей Y, Z:

DQg = ~[t + crfWy fjdxdydzdx

DQz = — d + Cppwt^dxdydzdx.

Общее количество тепла, подведенное к элементу объема за время йъ конвекцией, представим уравнением

+

Д Ытх) , д(ср? ии) д(срра>г)

Дх 1 ду дг

+

С"р Тх + Ту + Шг й) йхйУйгйх-

Определим количество тепла, вносимое в элемент объема тепло­проводностью через нижнюю грань в направлении оси X за время йх‘.

<3, = ~хйуйгй т.

Ограничиваясь двумя первыми членами разложения в ряд Тейлора ■ Ы

Функции получаем количество тепла, перенесенное теплопро* водностью через верхнюю грань за время

С1>+йх = А ^ dxd. ydzd.-t.

Приращение количества тепла в элементе объема вследствие переноса теплопроводностью в направлении оси X находим из уравнения

Д

DQx = Qx-^-dx Qx ~ ^ ^ dxdydzd'z.

Аналогично определим приращение количества тепла в элементе объема вследствие переноса теплопроводностью вдоль осей V, Z

= ЪуКТуйхс1ус1^''

DQz = ^ X ~dxdydzdz.

Тогда общее количество тепла, вносимое теплопроводностью в эле­мент объема, выразим уравнением

^ = [тхХ Тх + щ1 Гу + к1 и Шум*.

Суммарное количество тепла, внесенное в элемент объема за время d-.,

А/ , а* , 1ЮхТх+т«Ту + Dxdydzd-.

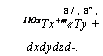*—{*№+г4^й+ЭД+«

А* ’дг

Dxiydid-. + [* X* + + |х|

Это количество тепла равно изменению энтальпии рассматрива­емого элемента объема:

DQ = c’pp*dxdydzJ^ dz

(с'р, р* — среднеинтегральные по элементу объема величины). При­равнивая выражение для йС1, после преобразований получаем

.•..Л, Лд(сР?®х) , 5(сР№у) , д(срр»01 ,

Ы дг + Гх 1 Ту 1 Гг ] +

. Г д( . , дС д. д( . д, д1 , д, д1 ~

+ Ср? ГхТх + ™УТу + ШгТг-Тх1Тх+Ту1ГУ + Тг1Тг <1<7)

Уравнение переноса тепла в движущемся потоке называется уравнением Фурье — Кирхгофа. При постоянстве теплофизических параметров ср, р, X оно принимает вид

д1 , д/ . д( дЛ „ оч

Ы Ы + ш*Ту + Гг = ^ Л 0 -®)