Коэффициент теплопередачи
 4 мая, 2013
4 мая, 2013  admin
admin Для расчета количества тепла, проходящего через стенку, по вышеуказанным формулам передачи тепла теплопроводностью необходимо знать температуры поверхностей стенки. Но в большинстве практических случаев эти температуры не известны; известны лишь температуры сред, омывающих стенку с обеих сторон. Примером служит паропровод, в котором известна температура пара и внешнего воздуха, но не известна температура трубы и изоляции. Подобными примерами служат также конденсаторы и другие теплообменники. Если температуры ограничивающих поверхностей не известны, то вводя так называемый коэффициент теплопередачи, количество тепла, переводящее от одной среды к другой через однослойную или многослойную стенки, определяем по формуле
<2 = /? . и (іг — 1В) ккал/час, % (27)
Где & — коэффициент теплопередачи, ккал/м2 • час °С;
—температура среды, отдающей тепло, °С;
(в —температура среды, воспринимающей тепло, °С Коэффициент тепло/передачи & состоит из коэффициентов теплоотдачи (среда — стенка, стенка — среда) и теплового сопротивления стенки.
Плоская стенка
Количество тепла, переданное за 1 час через однослойную плоскую стенку, которая отделяет среду, отдающую тепло, от среды, воспринимающей тепло, составит: ‘
|
(28) |
![]() Р - ([4]Г-А0
Р - ([4]Г-А0
|
1 |
![]() Ккал/час.
Ккал/час.
1
■ + - Т- + -
Сравнивая это уравнение с расчетным уравнением (27), для коэффициента теплопередачи к в случае однослойной плоской стенки получаем выражение
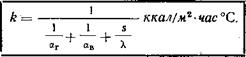 (29)
(29)
В этих уравнениях:
^ — поверхность нагрева, м2
*г — температура среды («газ»), отдающей тепло, °С; tв — температура среды («воздух)», воспринимающей , теи - ло, °С; ;п
Аг — коэффициент теплоотдачи среды, отдающей тепло («газ» — стенка), ккал/м2 • час • ° С; ав — коэффициент теплоотдачи, воспринимающей тепло (стенка— «воздух») ккал/м2•час-° С;
5 —толщина разделяющей стенки, м;
% — коэффициент теплопроводности материала разделяющей стенки, ккал/м2 • час • ° С. • -
Вывод. Если /1 °С — температура поверхности'стенки на стороне тепло- отдающей среды и °С — температура поверхности на стороне тепловоспр^- нимающей среды, то количество тепла, получаемое стенкой за 1 час, согласно уравнению (1) составит, 1
О = /3* - «г - (/г— /г) ккал/час. ‘V ~
Так как состояние теплового потока предполагается установившимся, та такое же количество тепла должно передаваться путем теплопроводности и через стенку [уравнение (2 а)]: . - щ.;«
* ’/.-•«г 4Д ' •
РАЗДЕЛЬНОЕ РАССМОТРЕНИЕ СПОСОБОВ ПЕРЕДАЧИТЕй^А
Количество тепла, воспринимаемое второй средой, должно быть равно предыдущему. Тогда, согласно уравнению (1),
(2 = ^ • ав (*2 — *в) ккал/час.
Из этих уравнений следует:
|
^ • аг О • Д • X О |
![]() /г —=-
/г —=-
Ь — ^2 —
/2 tвz=
Р аБ
Складывая эти уравнения, получаем
0.1 1 в 1
<Г-<в=— • (-+Т+^)-
Если решать относительно ф, то получим искомое уравнение (28).
Для многослойной плоской стенки, применяя обозначения, данные на рис. 1, получим следующее количество тепла, проходящее через нее,
<2 —--------- :---------------------------------------------------------- ккал/час. (30)
1 I ^ . в2 . 5з
Аг Л1 ^2 Лз
Подставляя в это уравнение уравнение (27), получаем для коэффициента теплопередачи через плоскую стенку, состоящую из нескольких слоев, которая разделяет две жидкости или два гада с коэффициентами теплоотдачи аг и ав, следующее выражение:__________________________________
|
|
Вывод. Пользуясь обозначениями, данными на рис, 1, находим количество тепла, отдаваемое газом с температурой tГ0C стенке, температура которой и °С [по уравнению (1)]
0 = р • аг • (/г — ккал! час.
Так как тепловой поток предполагается стационарным, то везде будет идти количество тепла, равное вышеприведенному. Количество тепла, проходящее через первый слой стенки,
(2 — ^1 (^1
~~ *1 '
Количество тепла, (проходящее через второй слой, *
Количество тепла, проходящее через третий слой,
^-Х3(/3-<4)
Количество тепла, отдавае! Мое третьим слоем внешней среде с температурой tв, согласно уравнению (1)-, составит
Ф • ав 4 /в).
Из этих уравнений следует:
<2
|
1 — с ’ Г • аг С • ®1 |
![]()
|
<ї ■ в» : () • $3 Ґ • х3 ; <2 |
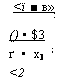 {г
{г
(г~13 = /3 — ^4 =
5 • а„
Суммируя, эти выражения, получаем
|
(~ + Т - + Т - + Т" + “)°С аГ 3 аВ / |
![]() , . <? / 1 ,^1 . «2 •г —‘в - р
, . <? / 1 ,^1 . «2 •г —‘в - р
Решение этого урарвяения относительно (2 даст нам искомые уравнения (30) и (31).
Температуры на поверхности и между отдельными слоями из этих уравнений получаются следующим образом: температура левой поверхности (см. рис. 1)
TOC o "1-5" h z = °С; (32)
Г • аг
Температура на границе ‘первого и второго слоев
К = (33)
^ • X,
I
Или, подставляя вместо и значение из уравнения (32), получаем '2 = *г—+т~)°с - (33а)
И аг Хх /
Аналогично определяется температура между вторым и третьим' слоями
И температура правой поверхности и
+ . (35)
Г ■ “в
Формулы ^ля расчета температуры в стенках, разделяющих две обменивающиеся теплом среды, еще раз приведены ниже (см. уравнения (480)—(487).
Цилиндрическая стенка
Количество тепла, проходящее через многослойную стенку трубы длиной 1 м, определяется по следующей формуле (обозначения см. на рис. 2):
=---------------- —([5]Г ~ *----------------------------- ккал/м ■ час (36)
1 . 1,151 )еЛ2 1,151 1£ а, ,1
^1 • °Г ^1 Х2 ^2 (1п+1 ав
Или согласно уравнению (22а) записываем формулу без логарифмов
О =--------------------------- (-г + *в1-------------------------- ккал/м-час.
1 , (<4 — с^) У1 (<*3 — 4) • Фг 1
' • ^ аг + (<*2 + йг) • Хх + (4* + • X2 ' ' ^п+1“в (36а)
|
Коэффициент теплопередачи в случае многослойной цилиндрической стенки, отнесенный к 1 пог. м, находим из уравнений (36) и (27):
|
Это уравнение, как и уравнение (36), отличается от уравнения П4), служащего для той же цели, тем, что в него введены коэффициенты теплоотдачи, так как в уравнении (14) даны температуры на поверхности стенки, а <в уравнении (37), напротив, даны лишь температуры окружающей стенку жидкой или газообразной среды. Если в уравнение (36) или (37) подставить не /г, а температуру стенки t, то получим а=оо. Следовательно, в данном случае tг—t^ и —-— =0. Из уравнений (36а) и (27)
Аг •
Можно получить приближенную формулу для определения коэффициента теплопередачи в случае, когда длина трубы составляет 1 м:
(<(, —«УЯ»! (* — </.) Ф* ,
*• /л. л і "Г • • • “Г
^1 аг № "Ь ^і)^ 1 (^3 + ^г) ^2
Ккал/М'час°С. (37а)
Значения в первом приближении могут быть овзяты равными единице, а более точно — из табл. 1 (стр. 32).
Вывод. Количество тепла, отдаваемое средой за 1 час внутренней поверхности трубы длиной 1 ж, составляет:
(2 = ^ ’ 1С ‘ аг ' (/г — /х) ккал/м • час.
Вследствие установившегося состояния через отдельные слои стенки должно передаваться такое же количество тепла. Следовательно, для первого слоя, согласно уравнению (4):
2729 X
(2 --------- ------- -— . _ /2) ккал/м • час
'«•Г
“1
Или по уравнению (19)
• П • (с?! -|- ) • (^1 /2)
Количество тепла, проходящее через второй слой,
2,729 Х2 (? = - ■ —-а— (/,-*,);
, “3
1б~Г
Через третий слой
У==_217^Х1
^7-
Из
Количество тепла, передаваемое поверхностью трубы внешней среде,
|
С1г п аг |
![]()
|
Из этих уравнений следует I Т —. = |
Т 12
2.729 • Хх *
Л і ___ “2 .
2.729 . Х2 *
<*4
<Мб.
А<
/3-/4-
4“~ 2,729-Х8 <?
Л • С?4 • ав
Складывая вышеприведенные уравнения, получаем
, 18т - 1ет - '8т - т
йі • те • аг 2,729 • Хх 2,729 • Х2 2,729 •' Хз ^4 * 11 * ав
Или,
('г-*в)*
TOC o "1-5" h z 1 1 1,151 1.151 в <?3
+ —— -18-^+—і •!е^_ +
• Яр ^4 * ®В ^1 ^1 ^2 ^2
-------- ГШ—1Г - (38)
+ _ТГ.-18^7
Тем же методом выводятся уравнения без логарифмов (с фактором ф).
Труба, »состоящая лишь из одного слоя, характеризуется диаметрами й и й2. В этом случае уравнение (36) преобразуется в выражение:
((г — /й) тс
TOC o "1-5" h z ^------------------------------ —_______ ККал1м • час.-------- (39)
1 1 , 1,151 , й2
* ®в ^1
Таким же образом определяется количество тепла, проходящее через стенку трубы длиной в 1 м, состоящую из двух слоев (п—2):
<2 =----------------------- (*‘~ ~<в)' я------------------- ккал/м - час. (40)
1 , 1,151 , ^ 1,151 й3 1
~т~~ Н—- • ^ "т“ + - г— • ^ — + —
“1 ат Х^ а7 Х2 а2 «з ав
Температуры на поверхности и на границе между отдельными слоями стенки находятся из уравнений, ‘Приведенных выше. Так, температура внутренней поверхности
К = <г - -7-^--------------- • ' (41)
“1 :11 [6] аг
Температура между первым и вторым слоями
1
<#8
Т
TOC o "1-5" h z ^ = ^—(2--------------- (42а)
2 1 4 2,729 Хх ' ’
Применяя приближенный метод с использованием уравнения (33а) для плоской стенки, получим
И - ^ —<}---------- 1----------- +----------------------- 1 (426)
[ • п • аг ((12-*г (1г) • ХХ7С ]
Температура между вторым и третьим слоями
1£ ^
= (И------------------ :----- 1-------- I ^ (43)
' ^паг 2,729 ■ 2,729 Х2/ '
ШГИ
18 Iі “2
(43а)
Или приближенно
К=^-0.—-±--------------- + ы 127Д ■ + -7ГТЛ1?—1- <43б)
I йх • тг • аг (а2 + «1) • *1* (а3 + а2) Л2 • тс ]
Температуру внешней поверхности получаем либо продолжением этого метода, либо проще, путем обратного расчета от известной температуры /в внешней среды: тепло течет в направлении, обратном указанному здесь, т. е. извне во внутрь трубы, то значение Q будет отрицательным. Примеры на стр. 427—437 иллюстрируют практическое применение выведенных уравнений.
Е. Практические выводы из анализа коэффициента теплопередачи
Можно сказать, что для анализа процессов теплопередачи знание величин, входящих в коэффициент теплопередачи, имеет такое же первостепенное значение, как закон Ома для электротехники. ^Поэтому © этом разделе подробно объясняется сущность коэффициента теплопередачи. Коэффициент теплопередачи в простейшей форме выражается уравнением (29):
K = ---------- о------- ккал/м2 • час °С.
Ils
«Г ав X
Оно охватывает все виды теплопередачи через плоские или только слабо изогнутые однослойные стенки.
Сущность коэффициента теплопередачи можно особенно хорошо раскрыть путем сравнения с соответствующими составными частями электропроводности. Из закона Ома известно, что при данном сечении проводника сила тока пропорциональна напряжению и обратно пропорциональна сопротивлению. При этом сопротивление равно сумме отдельных сопротивлений. Но это соотношение формально аналогично уравнению (28), определяющему теплопередачу, если вместо падения напряжения в законе Ома подставить разность температур tT—tB и вместо сопротивления
1 s 1
W — выражение--------- 1--- 1---- . Тогда количество тепла О =
Аг X ав
= --г-~ — - . Аналогия идет еще дальше, если это общее сопро
Тивление, которое приравнено к тепловому сопротивлению теплопередачи,
W = ——1—— ц——
' X
Состоит из отдельных частных сопротивлений:
Wt = —, = -f, г3 = -1.
Аг X, ав
Для других случаев, например для двухслойной цилиндрической стенки, эта сумма частных сопротивлений, согласно уравнению (36), будет равна
Ур = ______ -______ (- —— . + 1,151 . ^ + - 1
Й{ • к • аг тс. Х1 с1{ тс • Х2 й2 ^Зтеав
Замечателен тот факт, что при очень различных значениях частных сопротивлений лишь самое большое частное сопротивление имеет решающее влияние на теплопередачу. В котле, например, коэффициент теплоотдачи ав (на стороне воды) равен 5000 ккал/м2 • час *° С, т. е. соответствующее частное сопротивление =0,0002, в то время как коэффициент теплоотдачи аг
5000
(«а стороне топочного газа) имеет величину порядка 30; следовательно, соответствующее частное сопротивление — =0,0333
30
Примерно в 160 раз больше, чем на стороне воды. Так как толщина листового железа очень мала (5=0,02 м)у а коэффициент
Теплопроводности высок (А,=40), то соответствующее сопротив-
5 0,02 ЛЛЛЛ-
Ление — =--------- =0,0005 — »величина такого же порядка, что
А 40
И сопротивление на стороне воды. При этих значениях
£ —__________ *__________ 29 4
0,0002 4-0,0333 + 0,0005 ’ ’
Т. е. довольно точно совпадает с наименьшим коэффициентом^ теплоотдачи аг. Причина заключается в том, что величинам^-
0, 0002 и 0,0005 можно пренебречь по сравнению с 0,0333. Поз му в различных случаях теплопередачи необходимо знать в$ чины отдельных частных сопротивлений, чтобы была возмё! ность сделать правильные выводы. Так, например, в только ч разобранном случае анализ величины & сразу же позволяет сдЩ лать следующие выводы: для улучшения теплопередачи повышение коэффициента теплоотдачи на стороне воды ав путем особого расположения поверхности нагрева или увеличением скорости циркуляции воды не имеет решающего значения. При бесконечно большом коэффициенте теплоотдачи ав коэффициент теплопередачи останется практически неизменным, так как вели-
1 1 чинои — — ■ по сравнению с — практически можно пренебречь с таким же успехом, как и величиной —— по сравнению *
Оо
С — . Ясно, что и уменьшение теплового сопротивления листо - 30
Вого железа не приведет к повышению коэффициента теплопередачи, Следовательно, нет никакого смысла применять особенно тонкий и хорошо проводящий тепло листовой металл с целью улучшения теплопередачи. Действительное повышение & достигается лишь увеличением аг, т. е. улучшением теплоотдачи от топочных газов.
Иначе обстоит дело, например, в конденсаторах. Здесь коэффициенты теплоотдачи с обеих сторон поверхности нагрева высоки: например, на стороне воды ав = 5000 и на стороне пара аг = 10000 ккал/м2>час °С. Если бы (что практически не встречается) такой конденсатор изготовить из котельного листа тол - щиной 20 мм, то
А ------------------------------- : = 1250 ккал/м2 * час °С,
1 TOC o "1-5" h z 1 1_
5000 + 10000 + 2000 0,02 ' 1 ~
Где------- = —— . Сразу видно, что здесь тепловое сопротивле-
40 2000 * 3
Ние стенки ——г больше, чем сопротивления —----------- и -------- ,
2000 5000 10000
И поэтому требуется повышение коэффициента теплопроводности материала и уменьшение толщины листа. Если вместо листового железа толщиной 20 мм взять, например, лист латуни тол-
«с 5 0,005 1 , 0
Щинои 5 мм, то - г~= ----------- =------------ и £ = 2650, т. е. в 2 с
X 80 13000
лишним раза выше, чем у конденсатора, выполненного из листового железа. На основании этого легко объясняется пагубное влияние загрязнений поверхности нагрева у теплообменников, характеризуемых высокими коэффициентами теплоотдачи с обеих сторон, например, в конденсаторах, обогреваемых паром, испарителях и т. д. Противоположностью этому является иримёр с котлом, где вследствие преобладающего влияния сопротивления теплоотдачи на стороне топочных газов тонкий слой накгопи, как показывает уравнение (31), не вызывает заметного уменьшения коэффициента теплопередачи. Для изолированной печи почти безразлично, расположена она на открытом воздухе или в закрытом помещении, так как тепловое сопротивление кладки и изоляции достаточно велико по сравнению с сопротивлением теплоотдачи к воздуху, окружающему печЬ. Исходя из вышеизложенного, коэффициент теплопередачи можно эффективно увеличить лишь следующими мерами.
1. Если сопротивления теплоотдачи —и ------------ и тепловое
Аг ав
Сопротивление теплопроводности стенки ——окажут-
*1 '2
Ся одного порядка, то повышение коэффициента теплопередачи возможно лишь путем уменьшения каждого сопротивления в отдельности.
2. Если сопротивления теплоотдачи очень различны, то коэффициент теплопередачи эффективно можно повысить лишь уменьшением большего сопротивления.
3. Уменьшение частных сопротивлений, —— или
В Г Лд Л
Повлечет за собой тем большее повышение коэффициента теплопередачи, чем больше первоначально было данное сопротивление по отношению к другим частным сопротивлениям.
Вывод. Для улучшения теплопередачи в первую очередь необходимо обращать внимание на самое большое частное сопротивление.

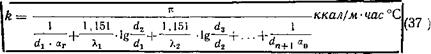
 Опубликовано в
Опубликовано в