МЕТОДИКА И СХЕМА РАСЧЕТА ПОЛИДИСПЕРСНОГО ФАКЕЛА
 4 мая, 2013
4 мая, 2013  admin
admin Аналитический расчет выгорания неизотермического трехмерного пылеугольного факела представляется в настоящее время практически невозможным. Для создания приближенного инженерного. метода расчета необходимо -построение правильной физической и математической модели процесса.
Комплексные исследования аэродинамики, динамики выгорания топлива. и теплообмена в призматических топочных 'камерах ларовых котлов (представленные в § 3-7) показали, что наиболее приближающейся к условиям развития топочного процесса является расчетная схема, разработанная В. В. Померанцевым, С. Л. Шагаловой и К. М. Арефьевым [31] и усовершенствованная авторами.
Эта схема учитывает влияние диффузионных и кинетических факторов на - процесс горения, а также взаимодействие частиц в полифракци -
Онном факеле, но построена она применительно к расчету одномерного факела.
В расчете принято, что в полидисперсном пылеугольном факеле частицы равномерно распределены в потоке и их температура равна температуре потока, время воспламенения топлива пренебрежимо мало по сравнению с общим 'временем его выгорания, .которое определяется длительностью горения крупных частиц коксового остатка.
Принимается первый порядок реакции по кислороду и считается, что конечным продуктом сгорания является С02. Внутреннее реагирование и горение окиси углерода - в расчете не учитывается, что допустимо для области температур, имеющей место при факельном сжигании твердых топлив в призматических тапках.
При принятых допущениях 'выгорание коксо, вых частиц размером £г - за время йт определится следующим выражением:
Л * 2 22’4 Ог, (9-1)
(>к I7 к 0,21
Ыид О
Где К = к = К*е —видимая константа скорости горения реакции
С+02 = С02, м/с; Мид — среднее для всех частиц полифракционного факела значение диффузионного критерия Нуссельта; 02—текущая концентрация кислорода, моль/м3; Ук — теоретический объем воздуха, необходимый для сгорания 1 кг кокса при СП, м3/кг; рк—'плотность кокса, кг/м3; О—коэффициент диффузии, м2/с*
При равномерном распределении частиц и кислорода по сечению факела концентрация кислорода одинакова для частиц всех фракций. Тогда из соотношения (9-1) следует, что
(»+N^)<Й' = (1 + - ИП7)‘''- <9-2>
Интегрирование соотношения (9-2) при отнесении константы скорости горения и коэффициента диффузии к средней температуре факела позволяет установить связь между размерами частиц любых фракций в полифракционном факеле. В промежуточной области
|
В диффузионной области &I &01 В кинетической области |
 ЕГ= |/(тект)^ - 1 + 2ЖГ--ЖГ’ Р-32*
ЕГ= |/(тект)^ - 1 + 2ЖГ--ЖГ’ Р-32*
^-=1>-1+*’, (9-36)
Об1
-%-=у-1+х, (9-Зв)
У— «о. ’ 501 ’
Йог и 8о1 — начальные размеры I-й и наиболее крупной из горящих в факеле частиц; 6г и 61 — соответственно текущие размеры этих частиц.
Характер выгорания частиц различного размера в полидисперсном факеле иллюстрируется рис. 5-17.
Из приведенных графиков видно, что три горении частиц в кинетической области эквидистантны кривые 6г = /7(т), а при горении в диффузионной—6г2 = ^(т) [31]. Следует помнить, что при полифрак - ционном факеле чисто диффузионная область горения имеет место только для самых. крупных частиц. При этом по мере их выгорания интенсифицируется диффузионный обмен и лимитировать процесс начинают кинетические факторы. Поэтому фактическое время горения частиц - несколько 'больше, чем то, которое получается по рис. 5-17
Установленная связь между скоростью выгорания г-х частиц и наиболее крупных значительно облегчила построение методики расчета времени горения полифракционного пылеугольного факела.
Рассмотрим состояние факела в. некоторый момент времени т, отсчитывая время с. момента входа (пыли в топку. К данному 'моменту времени в факеле, находятся и продолжают гореть только те коксовые частицы, которые имели размер, больший начального (6ог)т размера частицы, полностью сгорающей, к выбранному - моменту времени т.
![]() Общее количество несгоревшего кокса б (на 1 кг рабочей массы топлива) определяется следующим образом:
Общее количество несгоревшего кокса б (на 1 кг рабочей массы топлива) определяется следующим образом:
(9-4)
Это выражение после использования формулы (9-За) примет вид:
|
|
(9-4а)
|
Где
|
|
Уо (*)
|
-х5— = аД01 — коэффициент диффузионного обмена для начальной частицы
Оо1
Наиболее крупного размера; 1 — (^р —|— —|— Кр)—относительное
Содержание кокса на рабочую массу топлива, кг/кг; №р, Лр, Ур— относительное содержание влаги, золы и летучих на рабочую массу, кг/кг; /?о»—относительное массовое содержание (остаток на сите) частиц с размером, большим 6<н в исходной пыли.
Из общего количества несгоревшего кокса за время йх выгорает
|
|
(9-7)
|
(9-8> |
![]() С другой стороны, кинетическое уравнение для процесса выгорания факела можно записать следующим образом:
С другой стороны, кинетическое уравнение для процесса выгорания факела можно записать следующим образом:
Текущее значение произведения (приведенной константы скорости реакции Лпр на величину удельной поверхности. коксовых частиц »выражается формулой:
Ь°.1 к
= ф (9-9)
<г>о.)х 1 + Ь)цд О
Где йМ —число частиц /-й фракции в 1 кг исходного топлива; ^ — коэффициент формы.
Текущая концентрация кислорода в факеле с учетом расхода кислорода в факеле на горение летучих
К0.21 р 1 — и^Р РГ 1/о 1 10ч
Если использовать соотношение (9-3) при нахождении значений /Сор/7 и 02, то уравнение (9-8) можно привести к следующему виду:
. , К* 01
Кск Ычд Ох
- - йх, (9-11)
2 TOC o "1-5" h z =
Рдо1 и -{- /1 (х)
Р _ 1 РК Гг Д7ф 1-ЦУп 1 . 19
Ф 2 22,4 р!_^Р КрУ }
, 1Ч ’И 1 — и? л 1 /П 10ч
А=( аг—1)------------------- -, (9-13)
4 ' I к 1 — ^Р /СР ' '
где 1Л—объем газов, образующихся при сгорании 1 кг рабочего топлива при избытке воздуха на выходе из топки при СП, м3/кг; У0 — теоретический объем воздуха, необходимый для сгорания 1 кг рабочего топлива при СП, м3/кг; ат—коэффициент избытка воздуха в топочной камере; Тф—средняя эффективная температура факела, К; Р—давление в топочной камере, Н/м2; — газовая постоянная, Дж/(моль-К); рк —
Плотность коксового остатка, кг/м3, ф—коэффициент, учитывающий
Отличие формы частиц от шаровой.
Уравнение (9-11) (после интегрирования при средней эффективной температуре факела 'Приводится к виду:
|
Р5 |
![]()
|
01 |
![]() 1 .
1 .
Х
Для анализа тех случаев горения, .когда диффузионное сопротивление превышает кинетическое (горение высокореакционных топлив), выражение (9-14) удобнее представить в следующем виде:
( Иид Р ^
X
.где т—время выгорания факела, с; х—соответствующий данному времени конечный относительный размер наиболее крупной частицы.
Величина х связана с величиной механического недожога соотношением:
<3к т5^-/сР/*{х) =<ЗРн<7*’ (9‘16)
|
Где <3К и С? нр — теплотворная способность кокса и рабочего топлива, МДж/кг. Чтобы проинтегрировать правую часть выражений (9-14) - и (9-15), необходимо 'предварительно определить значения 'интеграла / (х). Вычисление /1(*)=0//(р производилось по начальному распределению частиц, так как число частиц любой фракции сохраняется неизменным до их полного сгорания. Опытные данные показывают, что распределение частиц пыли в тюлифракционно'М факеле вполне удовлетворительно выражается формулой Роз-ина—Раммлера: |
|
°*в D'Ql* DM ~firp °"9F 11 угольной пыли. Расчеты бы- |
|
Рис. 9-1. Значение интеграла Л(д0 ли произведены для значений Сплошные кривые — для кинетической области; штрихо - параметра NllflЦ/(/C6oi) — Вые —для промежуточной; штрих-пунктириые — для —()• 0 5’ I1 2 и ОО И В КЭЖ- Л ИшшУЗНОННОН ^ ^ * * |
|
Рис. 9-1. Значение интеграла 1(х) |
|
=0; 0,5; 1; 2 и °о и в каж- |
|
Диффузионной |
|
Г |
|
Ом |
|
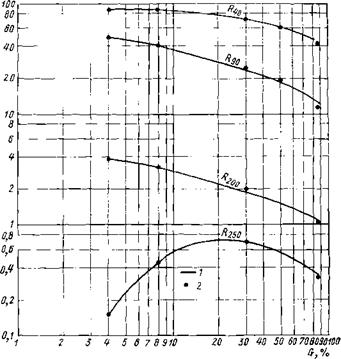
(9-5а) |
|
Этот интеграл целесообразно определять численным методом. Параметр т следует выбирать так, чтобы величина е~т была мала, т. е. |
|
Величина Яои соответствующая наиболее крупной частице размером 601, была близкой к нулю. Расчетный анализ показал, что при т>4,6 изменение т в широких пределах практически не влияет на конечные результаты интегрирования уравнения (9-14) и (9-15). |
|
|
|
|
|
|
 |
|
|
|
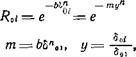
![]()
Дой из указанных областей реагирования «при п=0,8; 1,0; 1,2; 1,4 и 1,6. Значение параметра ї^ид/)/(/(6оі)->о° отвечает протеканию процесса горения в кинетической области. Для этого случая
1
|
/, (хУ |
![]()
|
(9-18) (9-19) |
![]() (у - +хуе~т» йу,
(у - +хуе~т» йу,
Уь-п Уо (X)
Уо (лг) =1 — х.
Величина Ыид/3/(Д'6о1)->0 соответствует условиям горения самых крупных частиц в диффузионной области. Значение интеграла Л (*)»•♦ определяется выражением
1
/, (л:)"1* = Тп | (уг — 1 + х*)3'2 е~ туП йу, (9-20)
Уо{*)
|
(9-21) |
![]() Уо (*) = V і —
Уо (*) = V і —
Интегрирование выражений (9-5), (9-18) и (9-20) .позволяет установить связь между величиной недожога 0=Кр1(х) и текущим относительным размером наиболее крупной частицы *=61/601. Значения Л (*)=/(*) при различных величинах п в кинетической, диффузионной и промежуточной областях реагирования представлены на рис. 9-1.
|
|
|
Рис. 9-2. Изменение фракционного состава пыли АШ в процессе выгорания (/?9о=12%; п= “1; бм“300 мкм; Лр = -12,7%) I — расчетные кривые; 2 — опытные точки |
С помощью этих графиков и формул (9-3), (9-6), (9-19) и (9-21) можно найти изменение фракционного состава пыли в процессе выгорания
С йЯ Г Ьі у
|
Л (*) |
] йу 301 ) Лу
Г <№ /■ 8{ у
3 Л, ( 501 ) Л»
Ро (Л)
|
/ К&01 = !{МГо) и |
![]()
|
Зависимости /2 = |
![]()
|
/2 |
![]()
|
V **оі ) Для п= 1, а = 0,1 и при разных /і (*) |
![]()
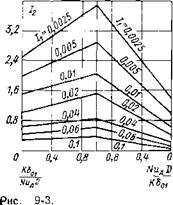 Кривые на рис. 9-2 характеризуют расчетное распределение частиц в полифракционном факеле при разной степени его выгорания. Опытные точки получены при исследовании динамики горения АШ в топочной камере парогенератора ТП-70.
Кривые на рис. 9-2 характеризуют расчетное распределение частиц в полифракционном факеле при разной степени его выгорания. Опытные точки получены при исследовании динамики горения АШ в топочной камере парогенератора ТП-70.
Зная величину /і(х), можно вычислить /г(х) и найти связь между временем выгорания факела т и относительным текущим размером наиболее крупной частицы х или между т и
<?р„ 1 1 — 1РП
С? к 7СР 1 — и^р При расчете горения в кинетической и диффузионной областях выражение (9-14) упрощается.
Время выгорания факела в кинетической области при средней эффективной температуре рассчитывается из соотношения 1
|
(9-23) |
![]() — / (У|КИЛ Г______________________________ ^______________
— / (У|КИЛ Г______________________________ ^______________
Рбо! 2{Л} “ } а + 1г(Х)к ин »
*
В диффузионной области
|
(9-23а) |
![]() ХЛх
ХЛх
А + 1Х (х)диФ
Результаты большой серии вычисления интегралов /2(х) при различных значениях параметров 1{х), а, п, Ыид£>/(/С601) и расчетный
|
К |
|||
|
-—1 |
»и 1 71 |
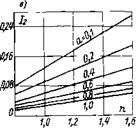 '0,8 1,0 и V Ц %<> 1>2 1,9 1,6 0#
'0,8 1,0 и V Ц %<> 1>2 1,9 1,6 0#
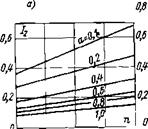
Рис. 9-4. Зависимости /а=/(я) для /1 (х) =0,06 и при разных значениях а: а — кинетическая область; б — промежуточная; в — диффузионная
|
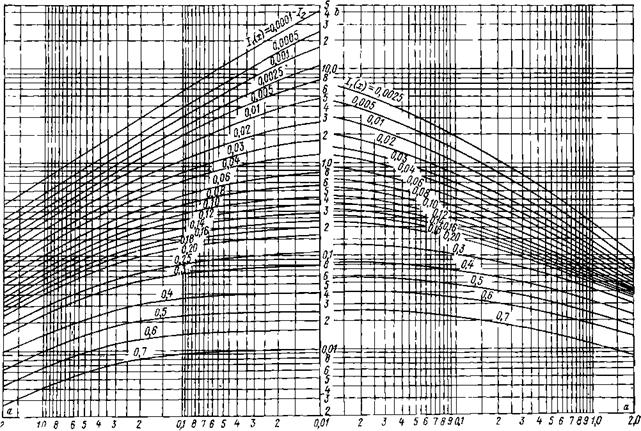
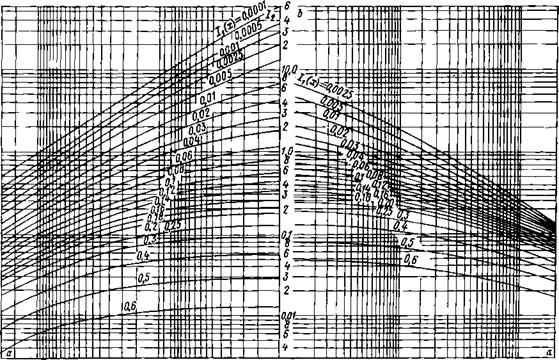
Рис. 9-5. Номограмма для расчета выгорания полифракционного пылеугольного факела в кинетической области (л=1) |
|
2 1р 8 6 5 4 3 2 0,18 765 4 3 2 0,01 2 3 4 5678 0,1 2 3 4 56 78 1,0 Рис. 9-6. Номограмма для расчета выгорания полифракционного пылеугольного факела в промежуточной области (/1 = 1) |
|
Рис. 9-7 Номограмма для расчета выгорания полифракционного пылеуголыюго факела в диффузионной области (л=1) |
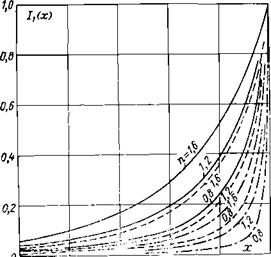
Анализ показали, что во всех областях реагирования существует практически линейная связь между величинами 1г{х) и Мид£>/(/СбоО (рис. 9-3), а также между величинами /г(^) и п (рис. 9-4). Это позволило разработать достаточно простую расчетную методику, основанную на использовании трех номограмм.
Номограммы, представляющие собой графики 12(х)=Р[а-, 1(х)] при п = 1, построены для МидО/^бо!)->оо (кинетическая область горения, рис. 9-5), для №илО/(К&о) = 1 (рис. 9-6) и для (диффузионная область горения, рис. 9-7). В правой части даны поправочные коэффициенты Ь, позволяющие вычислить 12(х) при п, не равных единице. Для расчетов при промежуточных значениях параметров N^£>/(/(601) и п можно воспользоваться методом линейной интерполяции.
Пользуясь этими 'номограммами, - можно произвести расчеты для определения времени горен-ия «различных топлив, разного фракционного состава в призматических топках при сухом и жидком шлакоудалении, а также 'проанализировать влияние на процесс горения таких режимных факторов, как тепло, вое напряжение топочного объема, коэффициент избытка воздуха и температура его подогрева, начальная - концентрация кислорода, рециркуляция топочных газов и другие.
Приведенные номограммы '.позволяют также производить расчеты динамики выгорания топлива по длине факела на тех его участках (на вертикальном участке), где справедливо допущение об его неоднородности, и сравнивать различные топочные устройства по интенсивности - процесса горения в них. При расчете по приведенным номограммам величины К, Р и О определяются при средней эффективной температуре факела.

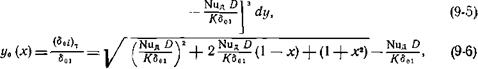

 Опубликовано в
Опубликовано в