1. Скоростные режимы работы мельниц

2. Траектория движения измельчающих тел при водопадном режиме.

3. Скорость падения измельчающих тел

4. Рудное самоизмельчение. Футеровка мельниц.

Механический режим работы мельницы характеризуют два основных параметра: относительное заполнение мельницы измельчающими телами и относительная частота вращения барабана. Относительное заполнение мельницы измельчающими телами равно отношению объема измельчающих тел к внутреннему объему барабана мельницы:

φ = V и / V. (3.2)

Здесь Vи – объем измельчающих тел, V – внутренний объем барабана, м3.

В свою очередь указанные объемы определяются из соотношений:

Vи = М и / γ и ; V = π D 2 L / 4. (3.3)

Здесь Ми и γи - масса и удельный вес измельчающих тел (для краткости далее рассматриваются шары); D и L – диаметр и длина барабана мельницы.

Тогда с учетом соотношений (3.3) имеем:

φ = 4 М и / γ и π D 2 L. (3.4)

Относительная частота вращения барабана ψ равна отношению фактической частоты вращения к условной критической частоте вращения:

Ψ = n / n кр. (3.5)

Критическая частота вращения барабана соответствует такой частоте, при которой сила инерции вращательного движения шара равна его силе тяжести. При этом шар, поднятый в самую верхнюю точку барабана, вращается вместе с ним как одно целое (центрифугирует), т. е. находится в динамическом равновесии и не отрывается от внутренней стенки барабана. При этом отсутствуют удары измельчающих тел по поверхности барабана и измельчение материала не происходит. Рассмотрим схему сил, действующих на измельчающее тело (шар, стержень, галю), в барабане мельницы (рис. 3.3).

С

Т

G

N

V

V

С

G

A

P

B

α

Рисунок 3.3 – Силы, действующие на измельчающие тела в барабане мельницы при его вращении

На шар при вращении барабана мельницы действуют следующие силы:

- центробежная сила

С = m V 2 / R ; (3.6)

- радиальная составляющая силы тяжести

N = G Сos α ; (3.7)

- тангенциальная составляющая силы тяжести

Т = G Sin α.. (3.8)

В соотношениях (3.6 - 3.8) приняты обозначения: V – окружная скорость вращения барабана, м/с; R – радиус вращения центра тяжести шара, м; α – угол между радиусом, на котором находится измельчающее тело (шар), и вертикальным диаметром барабана.

При неизменной частоте вращения барабана и отсутствии скольжения шаров относительно барабана центробежная сила С сохраняет свое значение и направление на всех участках круговой траектории (линия ВА). Величина и направление радиальной составляющей силы тяжести N изменяются и зависят от положения шара на круговой траектории (линия ВА). При некоторой скорости движения в точке А радиальная сила может сравняться с центробежной. Тогда шар под действием силы тяжести будет двигаться по параболической траектории АВ. Положение точки отрыва шара А зависит от угла α, который определяется скоростью вращения и размерами барабана.

В точке А:

С = N, (3.9)

M V 2 / R = G Сos α = m g Сos α , (3.10)

V 2 = R g Сos α . (3.11)

Но окружная скорость может быть определена из соотношения:

V = π R n / 30. (3.12)

Тогда после подстановки соотношения (3.12) в выражение (3.11) получим:

π 2 R 2 n 2 / 30 2 = R g Сos α , (3.13)

N 2 = 30 2 g Сos α / ( π 2 R ) ; (3.14)

N = ( 30 √ g Сos α ) / ( π √ R ). (3.15)

При достижении критической скорости вращения шар будет стремиться перейти на параболическую траекторию не в точке А, а в точке Р. Здесь α = 0, cosα = 1. В этом случае

N = n кр = ( 30 √g ) / ( π √ R ). (3.16)

Но √ g ≈ π. Значит

N кр = 30 / √R. (3.17)

С учетом того, что R = D / 2, получим из выражения (3.17):

n кр = 30 √2 / √D ≈ 42.3 / √D. (3.18)

Выразим скорость вращения n через n кр, используя выражения (3.17) и (3.15). Заменим в выражении (3.15) соотношение 30 / √ R на n кр . Тогда получим:

N = n кр √g Сos β / π . (3.19)

Здесь β – это такое значение угла α, при котором начинают отрываться шары внешнего слоя, непосредственно прилегающего к футеровке барабана мельницы.

С учетом того, что √g ≈ π будем иметь:

N = n кр √Сos β . (3.20)

На практике принимают n = (0.55-0.85) n кр. Существуют специальные расчетные таблицы значения критической частоты вращения барабана в зависимости от его размеров.

Относительная частота вращения барабана будет (см. выражение 3.5):

Ψ = n / n кр = √Сos β . (3.21)

Малоподвижное ядро

А

Б

В

N < n кр

N > n кр

При многослойном заполнении барабана измельчающими телами в зависимости от частоты вращении возможен один из следующих скоростных режимов движения измельчающих тел: 1) каскадный; 2) смешанный; 3) водопадный; 4) сверхкритический или махового колеса (рис. 3.4).

Рисунок 3.4 – Скоростные режимы работы мельниц

Каскадный режим (рис. 3.4, а) возникает при небольшом числе оборотов барабана. Измельчающие тела (шары, стержни, куски руды или галя) непрерывно циркулируют, поднимаясь по круговым траекториям и скатываясь каскадом вниз. При этом происходит перекатывание без полета. В центральной части шаровой загрузки образуется ядро, остающееся малоподвижным. Руда измельчается из-за раздавливающего и истирающего действия измельчающих тел.

Водопадный режим (рис. 3.4, б) возникает при частоте вращения барабана, обеспечивающей переход большинства слоев измельчающих тел с круговой траектории движения на параболическую с преимущественным полетом шаров. Измельчение происходит за счет удара падающих тел и только частично за счет истирания и раздавливания. Такой режим используется наиболее широко. Частным случаем водопадного является субкритический режим, образующийся при частоте близкой или равной критической. При этом режим движения внешнего слоя приближается к центрифугированию, шары движутся по круговым траекториям, высота их падения незначительна.

Смешанный режим – частично с перекатыванием, частично с полетом шаров.

Сверхкритический режим (рис. 3.4, в) или режим махового колеса появляется при частоте вращения барабана больше критической, с центрифугированием всего объема шаров. При этом работа измельчения равна нулю.

Траекторию движения тел при водопадном режиме необходимо знать для рационального профилирования футеровки барабана, выбора и расчета загрузочных и разгрузочных устройств, рационального заполнения барабана мелющей средой и пульпой, расчета прочности барабана. В качестве основной гипотезы движения принимается гипотеза Дэвиса. В соответствии с ней движение мелющих тел представляет собой цикл, состоящий из двух фаз: движение по параболической траектории (линия АВ) и движение по круговой траектории (линия ВА, рис.3.5).

V Y

V

V X

А

α

Х

В

R Cos α

R

O

Y

Рисунок 3.5 – Схема движения мелющих тел при водопадном режиме работы мельницы

Скорость в точке А - точке отрыва от круговой траектории - можно разложить на две составляющие V x и V y. Вдоль оси Y шар движется со скоростью V y = V Sin α , вдоль оси Х – со скоростью V x = V Cos α . Здесь α – угол отрыва, образованный вертикальным диаметром барабана и радиусом в точке А. Текущие координаты параболы:

У = ( V Sin α ) t – g t 2 / 2 , (3.22)

Х = ( V Cos α ) t. (3.23)

Здесь α - угол отрыва, t - время от начала полета тела. Из выражения (3.23) для х имеем:

T = x / V Cos α . (3.24)

Подставим выражение (3.24) в соотношение (2.22):

У = ( V Sin α ) t – g t 2 / 2 = ( V Sin α x / V Cosα ) – ( g x 2 / 2 V 2 Cos 2 α) . (3.25)

Ho V 2 = R g Cos α (см. соотношение 3.11), тогда

Y = x tg α – x 2 / 2 R Сos 3 α . (3.26)

Уравнение окружности с началом координат в центре барабана О имеет вид:

Х 2 + Y 2 = R 2 (3.27)

Уравнение окружности с началом координат в точке А имеет вид:

( х – R Sin α )2 + ( у + R Cos α )2 = R 2. (3.28)

После преобразований выражения (3.28) получим:

X2 + y 2 – 2 R x Sin α + 2 R y Cos α = 0. (3.29)

Положение тела в момент перехода с круговой траектории на параболическую определяется углом отрыва α. Положение точки падения В определяется ее координатами, которые можно определить, решив совместно уравнения параболы и окружности:

X B = 4 R Cos 2α Sin α , (3.30)

Y B = - 4 R Sin2α Cosα . (3.31)

На параболической траектории движения есть несколько характерных точек (рис. 3.6): точка А – точка отрыва шара от круговой траектории; точка В – точка падения шара на круговую траекторию; точка F - вершина параболы; точка Е – пересечение параболы с вертикальным диаметром; точка С – пересечение параболической траектории с осью х; точка D – пересечение параболы с горизонтальным диаметром. Координаты этих точек находятся из анализа уравнений круговой и параболической траекторий или путем их совместного решения.

А

А1

А2

В2

В

В1

Х

Y

V

F

E

C

D

α

α

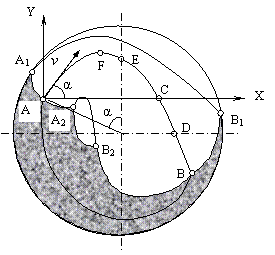Рисунок 3.6 – Характерные точки при движении измельчающих тел (к гипотезе Дэвиса)

Гипотеза Дэвиса дает удовлетворительное совпадение с результатами практики. Действительное движение измельчающих тел на участке перехода с параболической на круговую траекторию отличается от теоретического. Здесь наблюдается образование «пяты» (линия В1ВВ2), которая в реальных условиях имеет поверхность, близкую к плоской. Попытки усовершенствовать гипотезу Дэвиса не дали положительного результата.

Рассмотрим соотношение скоростей мелющих тел при их движении в мельнице (рис. 3.7). В точке А при переходе с круговой траектории движения на параболическую шар имеет скорость V . Удар происходит в точке В. При водопадном режиме работы на измельчение материала расходуется только часть кинетической энергии удара падающих шаров, которой они обладают в точке В. При падении шара на поверхность барабана или на другой слой шаров линия удара совпадает с направлением радиуса барабана ОВ. Линия удара – это прямая, проходящая через точку касания соударяющихся тел нормально к поверхности соприкосновения. Скорость падения VПад можно разложить на две составляющие: радиальную VРад, направленную по линии удара ОВ, и тангенциальную VКас, направленную перпендикулярно к линии удара, по касательной к круговой траектории. Шары в мельнице падают на подвижную, вращающуюся с окружной скоростью V, поверхность футеровки или на другой слой шаров с относительной скоростью VОтн . Относительная скорость связана с окружной скоростью и углом отрыва α зависимостью:

VOтн = 4 V Sin2 α . (3.32)

Направление относительной скорости проходит через точку отрыва А, т. е. через начало параболической траектории (по прямой линии АВ, см. рис.3.7). Составляющими относительной скорости также являются радиальная VРад и тангенциальная ( VКас – V ) скорости.

А

V

VРад

VОтн

V

VПад

VКас

VКас - VПад

O

B

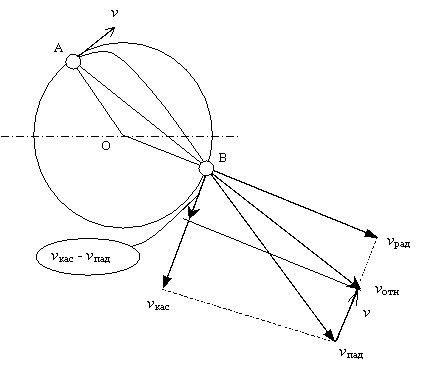Рисунок 3.7 – Соотношение скоростей мелющих тел при их движении

Радиальная скорость равна:

VPaд = 4 V Sin2α Sin 2α . (3.33)

Измельчение материала ударом шара происходит только за счет прямого удара, обусловленного радиальной скоростью VРад, действующей по линии удара. Тангенциальная скорость удара не производит и способствует только перемещению шара вдоль круговой траектории, если ее направление совпадает с направлением вращения барабана. При этом измельчение руды происходит за счет раздавливания и истирания. Вся кинетическая энергия шара в конце параболического пути равна:

E = m V2пад / 2 . (3.34)

Из этого количества энергии на измельчение ударом тратится только часть, равная:

Eyдара = m V2paд / 2 . (3.35)

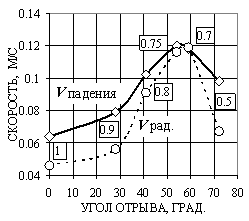Величины составляющих скорости падения мелющего тела зависят от относительной скорости вращения барабана мельницы ψ. Тангенциальная составляющая изменяется не только по величине, но и по направлению. На графике (рис. 3.8) представлено изменение величин скоростей падения и радиальной для стержневой мельницы с диаметром барабана 3200 мм.

Рисунок 3.8 – Изменение скоростей падения и радиальной в зависимости от угла отрыва при различных

Значениях ψ (приведены в рамках)

Относительная скорость вращения изменялась в пределах ψ = (0.53 – 1) nкр ; nкр = 24.5 об/мин для мельницы этого размера, угол отрыва при этом изменялся в пределах от 72 до 0о, соответственно. Как следует из графика, представленного на рис. 3.8, максимальные значения скоростей находятся в интервале ψ = (0.71-0.75) nкр, при α = 59-54о. При таком режиме максимальна и энергия удара.

Рудное самоизмельчение производится в мельницах большого диаметра и малой длиной (D = до 12м, L = 0.3-0.5D). При этом крупные куски руды являются измельчающими телами для более мелких и, разрушаясь, постепенно превращаются в готовый продукт. Процесс самоизмельчения принципиально не отличается от шарового измельчения. Основное конструктивное отличие мельниц самоизмельчения – наличие футеровки с высокими радиальными лифтерами (рис. 3.9).

Наличие лифтеров исключает скольжение крупных кусков по футеровке барабана, способствует их подъему на большую высоту при частоте вращения барабана 75-80% от критической. Барабан с высокими лифтерами работает как элеваторное колесо. В барабане мельницы самоизмельчения, так же как и в шаровых мельницах, существует практически неподвижное ядро и наблюдается сегрегация материала в поперечном сечении. При этом крупные куски концентрируются во внутренних слоях (II и III зоны) , а мелкие – во внешних слоях нагрузки (I и лифтерная зона).

Футеровка барабанных мельниц предназначается для : 1) защиты от износа барабана мельницы; 2) передачи энергии измельчающей среде; 3) сообщения траектории движения измельчающим телам, обеспечивающей наибольшую эффективность измельчения.

Профиль футеровки барабана зависит от крупности измельчаемой руды и размеров используемых мелющих тел, от частоты вращения и от диаметра барабана. Для мельниц, работающих в различных стадиях измельчения, необходим различный профиль футеровки. От профиля футеровки зависит величина скольжения мелющей загрузки и траектория движения шаров. Это отражается на мощности, потребляемой мельницей, и на эффективности ее работы. Основной задачей при выборе профиля футеровки является обеспечение максимальной производительности мельницы при минимальном износе и минимально допустимой толщине футеровки. Применяется стальная и резиновая футеровка различного профиля. Волнистую и унифицированную футеровки применяют при грубом измельчении, гладкую – при тонком. Срок службы стальной футеровки в зависимости от условий эксплуатации 1.5-5 лет. Срок службы резиновых футеровок дольше в 1.5-4 раза, а уровень шума шаров при мокром измельчении ниже в 2-3 раза. Масса резиновой футеровки меньше массы стальной в 4-6 раз.

ТЕМА 10. ТЕХНОЛОГИЯ ИЗМЕЛЬЧЕНИЯ

1. Схемы измельчения.

2. Определение циркулирующей нагрузки в схемах измельчения

3. Классификация в схемах измельчения

Схемы измельчения изображают в линейном виде или в виде схемы цепи аппаратов (схемы оборудования). Барабанные мельницы обычно работают в сочетании с операциями классификации, которые по назначению делятся на несколько разновидностей (аналогично операциям грохочения в схемах дробления). Классификация пульпы по крупности твердой фазы выполняется в механических спиральных классификаторах или в гидроциклонах. На практике применяют разнообразные одно-, двух - и трехстадиальные схемы измельчения. Многостадиальные схемы могут иметь открытый или замкнутый цикл измельчения в первой стадии. Разновидности применяемых схем зависят от крупности и свойств измельчаемой руды, а также последующей технологии обогащения. Существует большое разнообразие построения схем циклов измельчения. Рассмотрим некоторые примеры построения схем измельчения. На рис. 3.11 показаны некоторые варианты открытых одностадиальных циклов измельчения, а на рис. 3.12 - замкнутых. Рис. 3.12, б представляет собой схему оборудования для варианта 1-3 (рис. 3.12, а). На рис. 3.13 изображены замкнутые двухстадиальные циклы измельчения, на рис. 3.14 – трехстадиальный.

1 - 1

1 - 2

Классификация

Измельчение

Измельчение

Готовый продукт 1

Готовый продукт 2

А

Б

Рисунок 3.11 – Открытые циклы измельчения

Поверочная Классификация

Питание Мельницы

Слив гидроциклона, Готовый продукт

Пески

Слив мельницы

Зумпф

Насос

1 - 3

А

Б

Предварительная Классификация

Поверочная Классификация

Готовый Продукт 1

Готовый Продукт 2

В

1 - 4

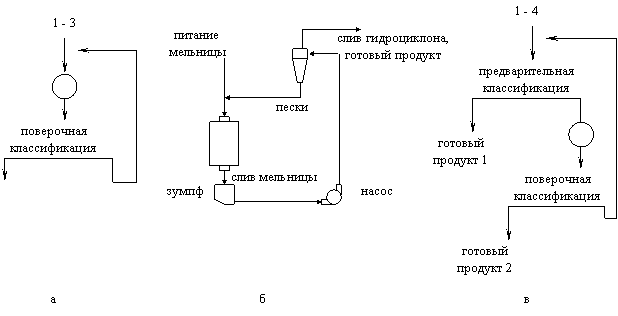Рисунок 3.12 – Примеры построения замкнутых циклов одностадиального измельчения

Классификация

Измельчение I

Измельчение I I

Измельчение I

Измельчение I I

Классификация

2 - 1

2 - 2

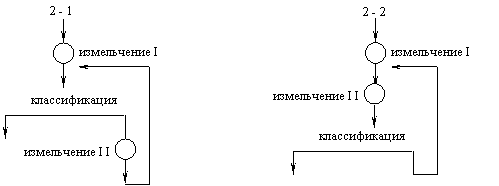Рисунок 3.13 – Замкнутые двухстадиальные циклы измельчения с открытым циклом в первой стадии

Измельчение I

Классификация

Классификация

Измельчение I I

Классификация

Обогащение

Концентрат

Отходы

Измельчение I I I

3 –3

Рисунок 3.14 – Замкнутый трехстадиальный цикл измельчения

Измельчение I

Классификация

Классификация

Измельчение I I

2 - 5

Q

S1

B1

A1

C1

Q

C2

Q

B2

S2

A2

Б

1

1

2

2

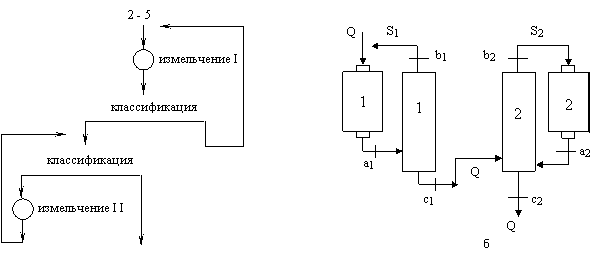
При установившемся режиме в замкнутых циклах циркулирует постоянное количество материала – циркулирующая нагрузка. Величиной циркулирующей нагрузки можно регулировать тонкость слива классификатора. Рассмотрим в качестве примера двухстадиальную схему измельчения с замкнутым циклом в первой стадии, вариант 2 - 5 в технологическом (рис. 3.15, а) и аппаратурном изображении (рис. 3.15, б).

A

Рисунок 3.15 – Двухстадиальная схема измельчения с замкнутым циклом в первой стадии

Слив мельницы первой стадии измельчения (рис. 3.15) направляется на классификацию в классификатор. Пески классификатора (зернистый продукт) возвращаются на доизмельчение – циркулирующая нагрузка. Слив классификатора первой стадии измельчения поступает в классификатор второй стадии измельчения. Пески классификатора 2 направляются на измельчение в мельницу второй стадии измельчения, а слив является готовым по крупности продуктом. Слив мельницы 2 идет на классификацию в классификатор 2. Введем обозначения: а1, b1, c1 – содержание класса – 74 мкм (0.074 мм) в соответствующих продуктах первой стадии измельчения, %; a2, b2, c2 - содержание класса –0.074 мм в соответствующих продуктах второй стадии измельчения, %. Обычно именно этот размер принимается за расчетный, т. к. готовый продукт должен содержать до 70-90 % класса –74 мкм (200 меш) в зависимости от вкрапленности и свойств полезного минерала и дальнейшей технологии обогащения.

Уравнение материального баланса по количеству класса –0.074 мм первого цикла измельчения:

( Q + S1 ) a1 = S1 b1 + Q c1 , (3.36)

Отсюда после несложных преобразований:

S1 = Q ( c1 – a1 ) / ( a1 – b1 ) . (3.37)

Уравнение материального баланса по количеству расчетного класса для II цикла измельчения:

( Q + S2 ) a2 = S2 b2 + Q c2 , (3.38)

Отсюда:

S2 = Q ( c2 – a2 ) / ( a2 – b2 ) . (3.39)

Математические зависимости для величины циркулирующей нагрузки являются индивидуальными и зависят от построения схемы.

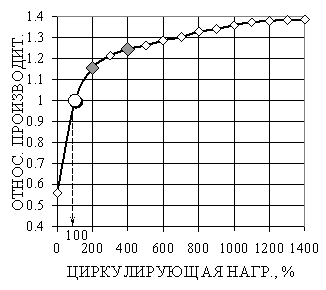Если обозначить относительную производительность мельницы при S = 100 % как Q = 1, то зависимость между производительностью мельницы и величиной циркулирующей нагрузки будет иметь вид кривой, асимптотически приближающейся к Q = 1.4 (рис. 3.16).

Рисунок 3.16 – Зависимость производительности мельницы от величины циркулирующей нагрузки

Циркулирующая нагрузка S может достигать 1200 %. При увеличении S от 0 до 400 % производительность мельницы по готовому продукту заметно возрастает. Затем при больших приращениях S производительность изменяется мало. Рекомендуемая циркулирующая нагрузка для первой стадии до 300 %, для второй – до 700 %.

4

3

2

1

Слив

Пески

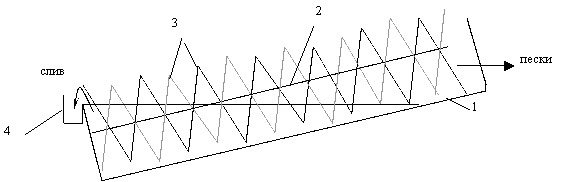Классификация в цикле измельчения применяется для разделения слива мельницы на два продукта по крупности. Механические классификаторы работают по принципу разделения твердой фазы пульпы в горизонтальном потоке на крупную фракцию – пески и на мелкую – слив. Разгрузка песков производится спиралью. Принципиальная схема спирального классификатора представлена на рис. 3.17.

1 – полуцилиндрическое корыто, 2 – вал, 3 – двухзаходная спираль, 4 – сливной порог.

Рисунок 3.17 – Схема устройства классификатора с непогруженной спиралью и высоким сливным порогом

Корыто классификатора наклонено под углом не более 18о. Вал вращается со скоростью 4-20 мин -1. Маркируются классификаторы по диаметру спирали и длине корыта. Бывают одно - и двухспиральные классификаторы в зависимости от необходимой производительности, могут работать в открытом или замкнутом цикле с мельницей. Различают классификаторы:

1) с непогруженными спиралями – вся верхняя половина витка спирали выступает над зеркалом пульпы. Применяются при крупности разделения 0.2 мм и выше.

2) с погруженными спиралями - участок спирали, находящийся вблизи сливного порога, целиком погружен в пульпу. Применяются для получения более тонкого слива (с содержанием более 65 % класса –74 мкм). С 1980 г. сняты с производства и заменяются более компактными гидроциклонами.

На работу классификаторов влияют: 1) наклон корыта классификатора; 2) высота сливного порога; 3) длина классификатора; 4) скорость вращения спирали; 5) нагрузка по пульпе; 6) разжиженность питания; 7) наличие шламов в питании; 8) удельный вес руды; 9) величина циркулирующей нагрузки.

Кроме спиральных классификаторов для классификации пульп применяются гидроциклоны – цилиндроконические аппараты для классификации тонкоизмельченных материалов в центробежном поле. Маркируются по диаметру цилиндрической части аппарата (ГЦ-75, диаметр 75 мм). Принципиальная схема гидроциклона представлена на рис. 3.18.

3

2

1

4

Слив

Питание

Пески

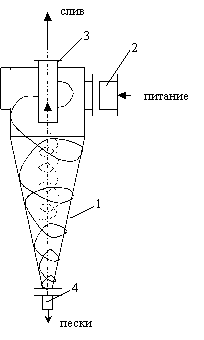1 – корпус, 2 -питающий патрубок, 3 – сливной патрубок, 4 – песковый патрубок (насадка)

Рисунок 3.18 – Принцип действия гидроциклона

Тангенциальный ввод питания от насоса под давлением создает в гидроциклоне вращательное движение пульпы с высокой угловой (тангенциальной) скоростью. Дойдя до вершины конической части аппарата пульпа, которая находится ближе к оси, изменяет направление своего движения, сохраняя вращательное движение. Этот поток поступает вверх в сливной патрубок, неся с собою у слив тонкие и легкие частицы. Режим движения турбулентный.

Вблизи оси аппарата тангенциальная скорость потока увеличивается настолько, что вдоль оси образуется столб воздуха. Скорость вращения потока вблизи оси аппарата одинакова по всей высоте. Поэтому воздушный столб имеет цилиндрическую форму.

Более тяжелые и крупные частицы прижимаются центробежной силой к стенкам аппарата и разгружаются через песковый патрубок, формируя пески или нижний (сгущенный) продукт. Насадки гидроциклонов съемные, их можно менять.

Основные факторы, которые влияют на работу гидроциклонов можно разделить на две группы: конструктивные и технологические. К конструктивным относятся следующие:

1) диаметр цилиндрической части гидроциклона,

2) диаметры патрубков – питающего, сливного и пескового,

3) угол конусности гидроциклона,

4) угол наклона оси гидроциклона к горизонту,

5) способ удаления слива,

6) давление на входе (напор).

К технологическим факторам относятся:

1) объемная производительность аппарата,

2) содержание твердого в питании,

3) гранулометрический состав питания,

4) вещественный состав питания.

При прочих равных условиях, чем мельче обрабатываемые частицы, тот меньше должный быть диаметр цилиндрической части гидроциклона.

Соотношение диаметров патрубков аппарата влияет на гидродинамику потока внутри него и соответственно на показатели распределения. Существует понятие – разгрузочное отношение, которое определяется как отношение диаметра песочной насадки к диаметру сливного патрубка D Песк / d сл. При увеличении разгрузочного отношения увеличивается выход песков с одновременным уменьшением их крупности и содержания твердого в них. Соответственно снижается крупность слива и его выход. Для обеспечения эффективной классификации подбирают оптимальное разгрузочное отношение.

Нижний край сливного патрубка должный быть погружен в гидроциклон немного ниже питающего патрубка. При увеличении глубины погружения сливного патрубка в гидроциклон происходит увеличение крупности слива.

Диаметр питающего патрубка в основном оказывает прямо пропорциональное влияние только на производительность аппарата. Качественные показатели классификации изменяются незначительно.

При увеличении угла конусности гидроциклона при прочих равных условиях снижается объемная производительность и выход песков с одновременным повышением крупности продуктов классификации. Гидроциклоны с большим углом конусности используются при обработке грубозернистых пульп, а с маленьким углом – для получения тонкого слива (10-20 мкм) в операциях обесшламливания. Обычно угол конусности в гидроциклонах, которые применяются для классификации и сгущения равняется 10-20о.

На обогатительных предприятиях гидроциклоны могут устанавливаться вертикально, наклонно или горизонтально. При наклонной или горизонтальной установке гидроциклона песковые насадки могут иметь немного больший диаметр для обеспечения таких же показателей распределения, как и при вертикальной установке аппарата. В этом случае пески содержат меньше тонких шламов и твердой фазы, а слив выходит более крупным.

На показатели работы гидроциклона заметное влияние может оказывать сливная труба. Чем больше перепад высоты между ее концами, тем более она действует как сифон. Значительный перепад оказывает содействие засасыванию в слив крупных частиц. Для обеспечения нормальной работы гидроциклона необходимо, чтобы диаметр сливной трубы был больше диаметра сливного патрубка.

Давление на входе (напор) в гидроциклон при заданной объемной производительности и параметрах насосной установки в основном определяется диаметрами сливного и питающего отверстий. Обычно на обогатительных фабриках работают с напором в пределах 0.05 – 0.15 МПа (0.5 – 1.5 кг/см 2 ). Для получения тонкого слива с высоким содержанием твердого необходимо поддерживать более высокие значения давления на входе.

Одной из характерных особенностей использования гидроциклонов в замкнутых циклах измельчения и классификации является то, что с увеличением циркулирующей погрузки на мельницу уменьшается извлечение расчетного (готового) класса в слив и эффективность классификации, однако удельная производительность мельницы растет.

Основным фактором, который определяет показатели работы гидроциклонов в циклах измельчения, является выход слива от операции. При увеличении выхода слива снижается разность между его крупностью и крупностью питания в данной технологической операции.

Для классификации рудных пульп используются гидроциклоны маленького диаметра небольшой производительности, которые объединяются в батарею. Обычное расположение гидроциклонов относительно питающей трубы - радиальное. Это обеспечивает более равномерное распределение питания. В практике углеобогащения используют низконапорные гидроциклоны диаметром от 350 до 1000 мм для сгущения, расположенные под небольшим углом к горизонту.