ГОРЕНИЕ ЧАСТИЦЫ ПЫЛЕВИДНОГО ТОПЛИВА
 20 апреля, 2013
20 апреля, 2013  admin
admin Горение частицы угольной пыли следует изучать в режимных условиях, близких к топочным и характерных для них. Для соблюдения характерного соотношения «топливо — воздух» рассмотрим горение частицы в среде воздуха, количество которого отвечает применяемым в топочной технике величинам коэффициента избытка воздуха, и в смеси этого количества воздуха с рециркулируемыми продуктами сгорания. Рециркулируемые газы, в которых коэффициент избытка воздуха составляет ат, количественно выражаются долей г от исходного объема воздуха в струе, вытекающей из горелки.
Смешением рециркулирующих продуктов сгорания с воздухом образуется газовая среда, реагирующая с частицей, которую назовем реагирующей газовой смесью. Объем этой смеси в расчете на 1 кг топлива — Уем. Начальная температура смеси 7Г.0, К, составляет:
Тг. = с*г' + гсгг’’. (16-1)
Св ~Г
Объемная концентрация кислорода в этой смеси С0, кг/м3, равна:
Ат— 1
В формуле:
Т! и Гр — температура исходной пылевоздушной смеси и рециркулирующих продуктов сгорания, К;
Г=Ур/У1— степень рециркуляции продуктов сгорания;
Ур — количество рециркулирующих продуктов сгорания, м3/кг;
— количество исходного воздуха, м3/кг;
Св и сг — теплоемкость воздуха и продуктов сгорания, кДж/(м3-К);
Сво — объемная концентрация кислорода в воздухе, кг/м3, при / = = 0°С и р = 0,1013 МПа;
Ат — коэффициент избытка воздуха в топке;
Уг — объем продуктов сгорания, м3/кт, который в общем случае определяется следующей зависимостью:
Уг = Квс. г4-(ат - 1)У-|-У,.„, (16-3)
Vв. п — количество водяных паров в продуктах сгорания, м3/кг.
В случае сухих топлив, когда объемом водяных паров без большой погрешности можно пренебречь, величина начальной концентрации кислорода в реагирующей смеси составляет:
От-- 1
1 + Г—----
С, = —1+г С. (16-2а>
Примем следующую логическую модель процесса. Реагирование протекает на поверхности частицы топлива сферической формы; частица в газовой среде находится в покое или движется вместе с ней с одинаковой скоростью; горение выделяющихся летучих и догорание продуктов неполного сгорания происходит в объеме газовой среды. Конвективный перенос тепла из системы отсутствует, а лучистый теплообмен моделируется взаимодействием реагирующей смеси с облучателем, температура которого принимается постоянной; теплообмен реагирующих частиц с газовой средой происходит путем конвекции и диффузионной теплопроводности.
Как известно, при очень тонком размоле углей зола топлива отделяется и поэтому в мелких частицах не содержится. Имея в виду также то, что в процессе приготовления угольной пыли топливо подсушивается, в расчетах принято, что в процесс горения вступают топливные частицы, состоящие только из горючей массы.
В начальный момент времени газовая среда имеет температуру,, значительно превышающую температуру частицы. Частица топлива воспринимает тепло газовой среды конвекцией и от облучателя — радиацией и нагревается. При этом из нее возгоняются летучие. Выделяющиеся летучие могут реагировать в газовой фазе, а твердая коксовая масса — в гетерогенном режиме.
В расчетах принята наиболее общая схема реагирования. Углерод реагирует с кислородом газовой фазы с образованием СО и СОг; получающаяся углекислота может реагировать с твердой фазой, образуя СО. Окись углерода, получаемая как в первичном, так и во вторичном процессах реагирования, вступает в химическое соединение с кислородом в газовой фазе. Принимается, что гетерогенные реакции и реакции, протекающие в окружающем частицу газовом объеме, идут по следующим итоговым уравнением.
Окисление углерода до СО
2С + 02=2С0 + (?1. (16-4)
349-
Окисление углерода до С02
С + 0(2, = СО2 + (2; 2. Восстановление двуокиси углерода
|
(16-6) (16-7) |
![]() СО2 + С = 2С0—<2и. Горение окиси углерода
СО2 + С = 2С0—<2и. Горение окиси углерода
Тепло химического реагирования, протекающего на поверхности частицы, передается конвекцией и диффузионной теплопроводностью окружающей газовой среде, радиацией облучателю и частично расходуется на дальнейший нагрев самой частицы. В результате температура частицы возрастает, причем это возрастание происходит тем более интенсивно, чем интенсивнее протекает химическое реагирование и чем меньше теплоотдача в газовую среду. В ходе реагирования диаметр частицы уменьшается, изменяются температура частицы, температура и состав газовой среды.
Предложенной логической модели процесса горения и принятым допущениям отвечает математическая модель в виде системы из следующих дифференциальных уравнений [Л. 51].
1. Уравнение кинетики выхода летучих из частицы
|
|
(16-8)
В уравнении:
Уг, Угв и (Уг—Угв)—количество летучих, первоначально содержащихся в горючей массе, выделившихся из него за промежуток времени т и содержащихся в частицах в текущий момент, кг/кг;
Ал — константы скорости выхода летучих, 1/с;
Т — текущая температура частицы, К;
Т — время, с.
2. Кинетическое уравнение горения летучих в га - зовойсреде
|
|
(16-9)
В уравнении:
Угс и (Угв—Угс)—количество летучих, прореагировавших (сгоревших) за время т, и количество летучих, содержащихся в газовой среде в текущий момент, кг/кг;
И - Е°!*Гг, ,
Асл—к0е — константа скорости горения летучих, 1/с.
3. Уравнение теплового баланса горения частицы
[((З'аЄЯ! 4-<3/2а2) Сд 0.'^ а2іС2^ X
XЩ Сг ~ (Т - Тг) - N114- (Г - Гг) - О0а? (Т* - 7*) - - І - 8Рк£к^ = 0.
(16-10)
В уравнении:
С^ь Q/2 и <3'21 — тепловые эффекты реакций образования СО и СОг и восстановления СО2, отнесенные к 1 кг кислорода, кДж/кг 02;
А!, аг и а21 — константы скоростей реакций образования СО, СОг и восстановления С02, м/с;
А = еа1 +аг —'суммарная константа скорости потребления кислорода по реакциям горения (16-4) и (16-5), 1/с;
8= 1 + С0+ С°2 учитывает увеличение числа молей при протекании реакций (16-4) и (16-6);
С0 и С°2 — начальная концентрация кислорода и углекислоты в реагирующей смеси, кг Ог/м3;
Сд и Сгд — концентрации кислорода и углекислоты у поверхности частицы (при 0°С и 0,1013 МПа), выраженные через содержание кислорода, кг Оа/м3;
Б, ,рк — текущий диаметр и плотность частицы, м и кг/м3;
Ск и сг — теплоемкость частицы, кДж/(кг-К), и газовой среды при 0°С и 0,1013 МПа, кДж/(м3-К);
Рг—плотность газов при 0°С и 0,1013 МПа, кг/м3;
N11 — тепловой критерий Нуссельта;
К — коэффициент теплопроводности газовой среды, зависящий от температуры по соотношению к = Хо + ЬТт,
Ао — коэффициент теплопроводности при 0,1013 МПа и 273 К, кВт/(м-К);
СГо = 5,67-10“11 — коэффициент излучения абсолютно черного тела, кВт/(м2- К4);
А, ф — степень черноты и коэффициент облученности, принимаемые равными 0,8 и 1,0;
Г и Гг — текущие температуры частицы и газовой среды, К;
Г0б — температура облучателя, принимаемая в расчетах равной 1773 К.
В уравнении (16-10) первым членом выражено тепловыделение при реагировании углерода до образования СО и СО2 по реакциям (16-4) и (16-5) и поглощение тепла при восстановлении СО2 на поверхности частицы по реакции (16-6); вторым —отвод тепла от частицы диффузионной теплопроводностью, расходуемой на нагрев кислорода и СО2, вступающих в реагирование с углеродом частицы; третьим и четвертым— теплообмен частицы конвекцией с газовой средой и радиацией с облучателем; пятым — расход тепла на нагрев частицы в единицу времени, отнесенный к единице ее поверхности.
Плотность горящей частицы можно определить, исходя из следующих предположений. Горение частицы сопровождается выходом летучих, несколько опережающим горение кокса. Если считать, что при выходе летучих объем сухой частицы не изменяется, то при полной возгонке плотность оставшегося кокса составит:
|
(16-11) |
![]() Рк-- Рг. м ( 1 УГ) 5
Рк-- Рг. м ( 1 УГ) 5
Где рг. м — плотность горючей массы топлива, кг/м3.
Выход летучих продолжается и заканчивается в процессе горения кокса. В промежуточный момент процесса горения частица состоит из кокса и невыделившейся части летучих. Поэтому плотность горящей частицы в промежуточный момент
|
(16-12) |
![]() Рч —- Рк -(- Рг. м (Уг — ^гв)-
Рч —- Рк -(- Рг. м (Уг — ^гв)-
4. Уравнение выгорания частицы кокса
^= -157 Ж К2**. +'*•) С* +'„1. (10-13)
|
5. Уравнение теплового баланса газовой среды
|
|
|
(16-14)
В уравнении:
— теплота сгорания летучих, кДж/кг;
С? Рн— низшая теплота сгорания топлива, кДж/кг;
#р и Лр — влажность и зольность топлива в долях от единицы, кг/кг;
С}' 12 — теплота сгорания реакции горения СО, приведенная к 1 кг кислорода, кДж/кг Ог;
У!' 12 — константа скорости реакции (16-7), 1/с;
Сх — концентрация СО в объеме, выраженная в кг 02/м3;
Яф — степень черноты газовой среды;
(З/У) ф — соотношение между поверхностью и объемом газовой среды, 1/м.
Первыми двумя членами в уравнении (16-14) выражены теплота, выделяющаяся при сгорании летучих и окиси углерода в газовом объеме; третьим и четвертым — диффузионная теплопроводность за счет потоков окиси углерода и углекислоты, образующихся по реакциям (16-4), (16-6) и (16-5), и летучих от поверхности частиц в газовую - среду; пятым — конвективный теплообмен между частицей и газом; шестым — лучистый теплообмен между газом и облучателем; результирующий седьмой член представляет собой изменение энтальпии газа за секунду.
6. Уравнение изменения концентрации кислорода.
Уравнение учитывает расход кислорода в реакциях образования СО и С02 на поверхности частицы и окисления СО и летучих в объеме
|
|
В уравнении:
V0л — теоретически необходимое количество воздуха для сгорания летучих, м3/кг;
7. Уравнение изменения концентрации углекислоты. Уравнение учитывает нарастание концентрации углекислоты за
Счет окисления углерода на поверхности частицы, окисления СО и летучих в объеме:
TOC o "1-5" h z ііСг —І*, Г п С /1 тхуР ЛР ^ 1
^ - и^2/г/ Гг аз0?к V1 - 1/см 1
+ х'1!С, + (^-Г)ас/»л(1 (16-16)
СМ
Необходимо отметить, что входящие в представленные уравнения концентрации кислорода и двуокиси углерода на поверхности частицы Ся и Сгя являются переменными величинами, текущие значения которых определяются начальными значениями соответствующих концентраций в объеме газовой среды и функционально зависят от протекания самого процесса реагирования. Размерность всех членов уравнения кг/ (см3 - К).
Конкретное нахождение этой функциональной зависимости является сложной задачей, требующей решения системы нелинейных дифференциальных уравнений, описывающей совместно с системой граничных условий концентрационные поля кислорода, окиси углерода и углекислоты в пространстве, окружающем горящую частицу.
Для линеаризации и решения данной задачи использовались упрощающие предположения и допущения, заимствованные из [Л. 43]. Эти допущения позволили дать искомые аналитические зависимости:
|
І — С°2 |
![]()
|
Со |
![]() (а2§ 20 4- 12Dd) 2О —-- VI2/)й2
(а2§ 20 4- 12Dd) 2О —-- VI2/)й2
С* =-- 1^^--------------------------- Г (|6-17>
И 4- 20) (а21д + 20) 4- 712ЕЙ |[(В + I) «1 + яг] § — — 3 + 2£>|
|
'2/? |
![]() Со М-2£) 4~ (2<1| 4~ ®2) 4“ С°2 [(а® “Н 2О) (VI2£)8 4“ 20) 4~ V12і§23
Со М-2£) 4~ (2<1| 4~ ®2) 4“ С°2 [(а® “Н 2О) (VI2£)8 4“ 20) 4~ V12і§23
(яй 4- 20) (а21д 4- 20) 4- 7і2Д5 | [(е 4- 1) Я, 4- о2] д —~ 3 4- 21)|
(16-18)
Концентрация СО определяется по балансовому соотношению,
КГ/М3,
С г == (Со — С — С г) —. (16-19)

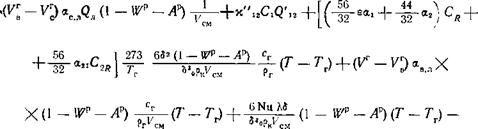
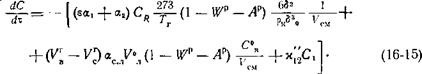
 Опубликовано в
Опубликовано в