ПЕРЕНОС ТЕПЛА И ПРИМЕСЕЙ В ТУРБУЛЕНТНОМ ПОТОКЕ
 10 апреля, 2013
10 апреля, 2013  admin
admin Одновременно с переносом количества движения при турбулентном перемешивании происходит перенос и других субстанций текущей жидкости: энтальпии и вещества жидкости, различных примесей в жидкости.
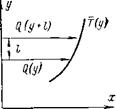
Предположим, что механизм переноса импульсов аналогичен механизму переноса тепла. Рассмотрим плоский поток, в котором температура изменяется в направлении оси у (рис. 6-2). Пусть частица жидкости из некоторого слоя, находящегося от стенки на расстоянии у, в котором среднее значение энтальпии составляет (2(у), перемещается перпендикулярно направлению потока на расстояние /т и внедряется в слой, где осредненное значе - ние энтальпии равно <) (у+17). ^
При таком перемещении частиц через единицу ных пульсациях ско - площади, нормальной к направлению оси у, за еди - рости.
|
(6-37 |
![]()
|
Ьху |
![]()
 = - п - р/2
= - п - р/2
Еицу времени будет перенесено тепла
?Т = V [<2(У) - <3 (</ + Ч] = - V” [<3 (</ + Ц - <2(£/)] = - VIт (6-38)
Слияние перемещающихся частиц с массой нового слоя вызовет ■изменение ее температуры, т. е. пульсацию температуры. Изменение температуры связано с изменением удельной объемной энтальпии уравнением
^^Q __ АТ ог\
-а» йор-*’ (6'39)
.где Ср — теплоемкость при постоянном давлении, кДж/(кг-К).
Подставив в уравнение (6-38) величину пульсационной скорости и величину изменения удельного теплосодержания согласно (6-11) и (6-39), получим для кДж/(м2-с):
|
Аи |
|
Срр1 |
|
Лу |
|
Тг (6‘40> |
Знак минус указывает, что тепло распространяется в сторону убывающих температур.
Перенос тепла указанным способом называется турбулентной теплопроводностью.
По аналогии с молекулярной теплопроводностью можно написать:
<7Т= — Ят—, (6-41)
-а величину Ят назвать коэффициентом турбулентной теплопроводности. Из сравнения выражений (6-40) и (6-41) видно, что
/ * №
Срр1т
|
Лу ІК |
![]()
|
Отношение ' Iю |
![]() (6-42)
(6-42)
|
Йу |
![]()
|
СрР |
![]() (6-43)
(6-43)
Называется коэффициентом турбулентной температуропроводности.
В потоке жидкости с неравномерно распределенной примесью при турбулентном перемешивании возникает перенос массы примеси, называемый турбулентной диффузией. Пусть в плоском потоке концентрация изменяется в направлении оси у. Частица жидкости из некоторого слоя у, в котором осредненная концентрация составляет С (у), кг/кг, перемещается перпендикулярно направлению потока на расстояние 1т' и внедряется в слой, где осредненное значение удельного содержания примеси равно С(у + 1т). При переходе частицы переносят примесь в количестве рУ'С(у). Частицы, двигающиеся в обратном направлении, переносят примесь в количестве
Р V'С [у + 1т) •
Осредненный результирующий поток примеси через единицу площади за единицу времени, называемый диффузионным потоком, составляет:
Ш, = рУ 1С(у)-С(у + Ц] = /т. (6-44)
Подставив величину пульсационной скорости (6-12), получим для тт, кг/(м2-с):
|
ЙС Лу |
|
Йу |
|
1 ■ ь V 1 Йу Формулу (6-45) можно переписатьв виде |
|
/72-г — р^т Введя обозначение ■<«7 |
|
<ю |
 |
|
|
|
Т?~—ет р (6-456)
Которая аналогична формуле молекулярной диффузии.
Величина ет имеет размерность коэффициента диффузии. Коэффициент турбулентной диффузии ет зависит от гидродинамических условий и поэтому является функцией координат.
Мерой интенсивности переноса какого-либо свойства являются соответствующие коэффициенты турбулентного обмена, которые обозначены: для переноса количества движения — ет; тепла — ея; массы — вт.
Если предположить, что механизм турбулентного обмена количества движения массы и тепла одинаков, то при этом, как видно из сравнения выражений (6-34), (6-43) и (6-45а), одинаковыми получаются ет, гд и ет. Однако опыты показали, что коэффициенты турбулентного обмена при переносе количества движения и при переносе тепла или примеси не совпадают, в частности, в случае свободной турбулентности єд/єт = 2, а Єт=Єд. По теории переноса завихренности коэффициент турбулентного обмена получается больше, чем по теории переноса количества движения, поэтому теория Г. Тейлора дает лучшее совпадение с опытными данными по коэффициентам переноса.

 Опубликовано в
Опубликовано в