КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
 24 марта, 2013
24 марта, 2013  admin
admin Теплообмен между движущейся средой и поверхностью твердого тела называется конвективным теплообменом или теплоотдачей. Конвективный теплообмен обусловлен совместным действием конвективного и молекулярного переноса теплоты (теплопроводности). Под конвективным переносом теплоты в среде с неоднородным распределением температуры понимают перенос, осуществляемый макроскопическими элементами среды при их перемещении, движении.
Различают движение вынужденное и свободное. Под вынужденным движением или вынужденной конвекцией жидкости понимают движение, вызванное действием внешних сил, приложенных на границах системы, поля массовых сил, приложенных к жидкости внутри системы, или за счет кинетической энергии, сообщенной жидкости вне системы.
Свободное движение или свободная (естественная) конвекция жидкости — движение под действием неоднородного поля массовых сил, приложенных к частицам жидкости внутри системы и обусловленных внешними полями (например, гравитационным).
Различают ламинарный и турбулентный режимы течения. При ламинарном режиме характер течения спокойный, слоистый, без перемешивания (от лат. lamina — полоска, слой). Ламинарное движение жидкости - это движение, при котором возможно существование стационарных траекторий ее частиц, часто повторяющих профиль канала.
|
А Ах Г f>K + tk, 1
|
При турбулентном движении течение жидкости неупорядоченное, вихревое (от лат. turbulentus - бурный, беспорядочный), с хаотично
изменяющимися во времени траекториями частиц, при котором в потоке возникают нерегулярные пульсации скорости и давления.
Переход ламинарного режима течения в турбулентный определяется значением числа Рейнольдса, которое называется критическим ReKp = vvKp//v. Чем больше Re, тем больше силы инерции по сравнению с силами вязкости, тем больше турбулентность потока.
Режим движения жидкости, промежуточный между ламинарным и турбулентным, называется переходным.
Течение жидкости состоит из основного потока и пограничного слоя. На твердой поверхности вследствие действия сил вязкого трения образуется тонкий слой заторможенной жидкости. Частицы жидкости, непосредственно прилегающие к поверхности теплообмена, как бы прилипают к ней. С возрастанием сил вязкости и, следовательно, с уменьшением числа Re происходит утолщение пограничного слоя. Чем больше Re, тем тоньше пристеночная область течения, тем тоньше пограничный слой.
Несмотря на то что пограничный слой остается тонким (а измерение скоростей показывает, что толщина его порой составляет несколько молекулярных слоев жидкости), он играет большую роль в процессах конвективного теплообмена.
Различают динамический и тепловой пограничные слои. Динамическим пограничным слоем называют пограничный слой жидкости, характеризующийся большим градиентом продольной составляющей скорости.
Тепловой пограничный слой характеризуется большим градиентом температуры, под действием которого осуществляется поперечный перенос теплоты. В области, непосредственно прилегающей к поверхности теплообмена, температура изменяется от гж — температуры основного потока до температуры стенки Tc. За пределами теплового пограничного слоя температура однородна и там явление переноса теплоты отсутствует. Тепловой пограничный слой по толщине 8Х может совпадать или не совпадать с динамическим 8 (рис. 2.28, 2.29). Соотношения толщин теплового и динамического пограничных слоев определяются значением числа Pr = V/A.
Как было показано выше, расчет теплоотдачи, несмотря на большую сложность процесса, проводится по формуле Ньютона - Рихмана
|
Щ |
|
Wo |
П ІП
Tr
У//////////////////Ш л
Рис. 2.28. Схема динамического пограничного слоя
Ш////////////У/////////Л х
Рис. 2.29. Схема теплового пограничного слоя
Достаточно простого вида
Q = а(гс~гж). (2.229)
Вся сложность расчета состоит в определении коэффициента теплоотдачи. Согласно (2.229), коэффициент теплоотдачи определяется как плотность теплового потока при температурном напоре, равном одному градусу. Перенос теплоты в вязком пограничном слое осуще в - ляется путем теплопроводности и в соответствии с законом Фурье определяется соотношением
Q = - X Dt/Dy. (2.230)
Сравнивая (2.229) и (2.230), получим коэффициент теплоотдачи
(2.231)
T-IK
В первом приближении можно принять градиент температуры в тепловом пограничном слое равным
Grad T = BjlJs., (2.232)
Ду 8Т
В этом случае коэффициент теплоотдачи будет определяться соотношением
Ос = У8Т. (2.233)
Величина а зависит от всех факторов, влияющих на сам процесс теплообмена. К ним относятся скорость движения жидкости, физические свойства теплоносителя, характеристики температурного поля и гидродинамические характеристики потока, геометрическая форма Ф и размеры / поверхности теплообмена:
Ос =/(<•„, р, р, X, w, t, Ф, I, р, (2.234)
Классификация задач конвективного теплообмена отражает преобладающее влияние перечисленных факторов. Для некоторых частных случаев эти задачи при упрощающих предпосылках могут быть решены аналитически методами теории пограничного слоя. В общем случае для этой цели используется экспериментальный путь определения а с применением теории подобия.
Порядок величины а [Вт/(м2 • К)] для различных условий конвективного теплообмена лежит в пределах:
Свободная конвекция в газах...................................................................... 5...30
Свободная конвекция для воды....................................................... 102...103
Вынужденная конвекция газов........................................................ 10...500
Вынужденная конвекция для воды......................................................... 500...104
Теплообмен при изменении агрегатного состояния воды (кипение, конденсация) 103 ... 105
Решение задачи конвективного теплообмена чаще всего дается в критериальной форме. Так, для теплоотдачи при свободной конвекции определяющим критерием является число Грасгофа и расчетное уравнение имеет вид
NUA./ —f(Gr, Рг)ж/.
Для вынужденного движения определяющим критерием является число Рейнольдса:
Nu./X, = /(Re, Рг)ж(. (2.236)
Для газов эти формулы могут быть упрощены, так как для газов число Прандтля слабо зависит от температуры. В этом случае зависимости будут соответственно:
Nu,, =/( Сг)ж); (2.237)
Миж/=ДКе)ж/. (2.238)
Индексы у критериев указывают на определяющую среднюю температуру жидкости гж, которая может быть получена принятым способом осреднения, и определяющий геометрический размер I.
Определение а и теплового потока на поверхности теплообмена является основной задачей теории конвективного теплообмена.
Теплоотдача при вынужденном движении жидкости вдоль плоской поверхности. При движении жидкости вдоль плоской поверхности профиль распределения продольной скорости поперек потока изменяется по мере удаления от передней кромки пластины. Если скорость в ядре потока Н'о, то основное изменение ее происходит в пограничном слое толщиной 8, где скорость уменьшается от w0 до wx = 0 на поверхности пластины. Течение в пограничном слое может быть как ламинарным, так и турбулентным. Режим течения определяется критическим значением критерия Рейнольдса, нижний предел которого для ламинарного пограничного слоя равен ReKp = 8 • 104, а при Re > 3-Ю6 вдоль пластины устанавливается устойчивый турбулентный режим течения. При значениях 8 • 104 < Re < 3 • 10б режим течения — переходный (рис. 2.30).
В турбулентном пограничном слое непосредственно на поверхности пластины имеется весьма тонкий слой жидкости толщиной 0,0018... ...0,018, называемый ламинарным подслоем, в котором силы вязкого
Трения играют преобладающую роль.
|
(2.235) |
|
Ламинарный подслой |
|
Рис. 2.30. Схема пограничного слоя с ламинарным подслоем |
|
Ламинарный режим |
|
Турбулентное течение |
|
Переходный режим |
При оценке толщины 8 пограничного слоя исходят из определения такой области течения, в пределах которой изменение силы вязкого трения по нормали к поверхности и изменение инерционной силы по направлению движения жидкости — величины одного порядка. Деление потока на вязкий пограничный слой и внешний потенциальный поток позволяет упростить математическое описание движения
жидкости. Так, в уравнении движения основного потока можно опустить члены, отражающие действие сил вязкости. Порядок уравнения понижается. Для пограничного слоя математическое описание движения также упрощается.
В процессе теплообмена наряду с динамическим слоем формируется тепловой пограничный слой. В пределах теплового слоя температура жидкости изменяется от температуры твердой поверхности fc до значения температуры невозмущенного потока жидкости T,K. Тепловой пограничный слой характеризуется большим поперечным градиентом температуры Dt/бу. За пределами теплового пограничного слоя толщиной 8, температура однородна и там явление переноса теплоты не возникает. Тепловой пограничный слой образуется аналогично динамическому. По мере удаления от передней кромки пластины толщина теплового пограничного слоя растет 8, —- F(X) вследствие возрастающего влияния поверхности пластины на прогрев жидкости.
При турбулентном пограничном слое основное изменение температуры происходит в пределах вязкого ламинарного подслоя.
Характеристиками переноса количества движения и теплоты являются кинематическая вязкость v и температуропроводность а. Поэтому соотношение толщин гидродинамического пограничного слоя и теплового пограничного слоя зависит только от значения числа Прандтля Рг = V/A. Очевидно, что чем больше число Рг, тем интенсивнее происходит перепое импульса движения в динамическом слое, тем больше поперечный градиент продольной составляющей скорости по сравнению с поперечным переносом теплоты. В этом случае толщина динамического слоя больше толщины теплового пограничного слоя. При малых значениях Рг тепловой слой может иметь толщину большую, чем динамический пограничный слой. При значении Рг = 1 толщина слоев одинакова. Практически толщины слоев одинаковы лишь для газов, у которых Рг близок к единице. Значения Рг для некоторых рабочих тел:
TOC o "1-3" h z Рабочее тело t °С Рг
Вода....................................................................... 100 1,75
180 1,03
350 160
Насыщенный водяной пар. . . 200 1,36
Воздух............................................................. -50... 300 0,733
Спирт..................................................................... 20 16,6
Глицерин................................................................ 20 10508
Ртуть...................................................................... 50 0,023
Натрий............................................. 450 0,005
Применительно к пограничному слою система дифференциальных уравнений теплообмена может быть существенно упрощена — в этом состоит значение понятия пограничного слоя и суть теории пограничного слоя, которая была заложена Прандтлем в 1904 г. и сначала касалась только гидродинамических задач.
Напишем дифференциальные уравнения теплообмена для динамического пограничного слоя на полубесконечной пластине. Расположим начало координат в передней точке пластины, ось направим вдоль
пластины (рис. 2.31). Рассмотрим безградиеитное течение dpfdx = О, тогда уравнение движения (2.35) для двухмерного стационарного течения при отсутствии объемных сил может быть написано в следующем виде:
Dwx Dwx D2Wx
|
W, |
|
Ду' |
|
Дх |
' - ■ * * (2.239)
+ wv
Ду
Уравнение энергии (2.22) для двухмерного пограничного слоя (при стационарном тепловом режиме) также существенно упрощается. В этом случае Dt/Dx = 0 и Dt/Dz = 0 (пластина бесконечна в направлении Z). В связи с малой толщиной теплового пограничного слоя 8, за основное изменение температуры можно принять изменение температуры по нормали к поверхности теплообмена. Тогда D2T/Dx2 <S:D2T/Dy2 и уравнение энергии примет вид
82t
|
Рис. 2.31. К подобию распределения скорости и температуры в пограничном слое |
(2.240)
Dt Dt
Ду'
Анализ уравнений (2.239) и (2.240) позволяет обнаружить подобие между распределением скорости и температуры в пограничном слое, если v = а или число Pr - 1. Уравнение движения и энергии при этом условии (Pr = 1) становятся идентичными. Это означает, что поля скоростей и температур в пограничном слое подобны, а кривые распределения безразмерной скорости и безразмерной температуры по толщине пограничного слоя одинаковы. Таким образом, физический смысл числа Прандтля состоит в подобии кинематического и теплового полей. Для газов число Прандтля практически не зависит от температуры и давления и определяется в соответствии с кинетической теорией газов атомностью газа: для одноатомных газов Рг = 0,67; для двухатомных Рг = 0,72; для трехатомных Рг = 0,8 и многоатомных Pr = 1. Из приведенных значений Рг следует, что полное подобие полей скорости и температуры сохраняется лишь для многоатомных газов. В других случаях имеют место отклонения от подобия. Точные решения дифференциальных уравнений пограничного слоя отличаются большой громоздкостью и сложностью. Приближенные решения могут быть получены из интегральных уравнений пограничного слоя. ,
—-
|
Рис. 2.32. К выводу интегрального уравнения энергии |
Идея интегрального метода теории пограничного слоя заключается в том, что с помощью приближенного описания распределения скорости или температуры по толщине пограничного слоя, используя некоторые простые интегральные соотношения, находят толщину соответствующего (динамического или теплового) пограничного слоя, а зная толщину слоя 8Т, согласно (2.233), нетрудно определить коэффициент теплоотдачи. Ниже приводятся выводы, справедливые для случаев Рг 1, т. е. для большинства технических жидкостей, а также для газов. При этом тепловой пограничный слой лежит внутри динамического пограничного слоя. Если же число Прандтля значительно меньше единицы, что имеет место у жидких металлов, то тепловой пограничный слой выходит далеко за пределы динамического пограничного слоя. Теплопроводность металлов оказывает решающее влияние на теплоотдачу и все зависимости, выведенные для случая 8 ^ 8Т, перестают работать.
Интегральное уравнение энергии для теплового пограничного слоя. Составим тепловой баланс для некоторого объема, выделенного в пределах пограничного слоя двумя сечениями 1—2 и 3 — 4, отстоящими одно от другого на расстоянии dx (рис. 2.32). Размер выделенного объема в направлении оси у равен H, причем H > 8Т и в направлении оси Z равен 1.
На основании закона сохранения энергии при стационарном тепловом режиме алгебраическая сумма тепловых потоков, проходящих через все плоскости, ограничивающие выделенный объем Dx - H- 1, равна нулю:
<2І-2 + <2З-4 + Є2-З + <2і-4 = 0, (а)
Где <21-2 — количество теплоты, вносимое через грань 1-2,— может быть выражено в виде
6l-2=foPCptWjed3'. (б)
На расстоянии dx изменение количества теплоты будет равно
^(J*pcpЈwxdj/)dx, (в)
Это изменение можно рассматривать как разность потоков теплоты QU2 и бз_4. Количество теплоты Q i_4, отдаваемой через плоскость 1-4 поверхности теплообмена, равно
= (г)
Поток теплоты через поверхность 2-3 может быть определен из соотношения
(>2-3 = Rn2.3CPTQ,
Где т2.З — масса жидкости, входящей через поверхность 2-3.
Величина т2.3 может быть определена по разности расходов ти2
И «3.4.
Поток массы через плоскость 1-2
Т-2 = J0H Pwx Dy.
|
J pwxdy^ It J pWjc dy^ dx. Дет J pw. xdy^dx. |
При прохождении расстояния dx поток массы изменится на вели
Чину
I Pw* dy I dx.
Dx
Тогда поток через поверхность 3-4 будет
Г" . D
Ща - J pwx dy + —
Поток массы через плоскость 2-3 будет
D
M2-З = w3.4 - M{.2 = —
Поток теплоты через поверхность 2-3 выразится соответственно уравнением f
62-3 = P^Wo Dyj dx. (д)
Подставив в уравнение теплового баланса (а) выражения (в), (г), (д), получим
|
РсрvvAi0 Dy] dx - ~ |
|
Dx |
, / L*H І / D
PCpVi^f dy J dx + Qc dx ■ 1 = 0.
0
|
D Dx |
После подстановки qc и некоторых преобразований получим окончательное выражение интегрального уравнения энергии для пограничного слоя:
"Br df
Wx (to - t)dy = A~~. (2.241)
В уравнении (2.241) верхний предел интегрирования заменен на 5Х, так как при H > 5Т температура потока постоянна и равна температуре невозмущенного потока f0. В этом случае стоящая под знаком интеграла разность температур обращается в нуль. Выражение (2.241) впервые получено Г. И. Кружшшным. Для динамического пограничного слоя решение задачи было получено Т. Карманом (1921). В случае пластины интегральное уравнение динамического слоя имеет аналогичное выражение :
D Ґ. , dw„
— j wx (vv0 - W) dy = V-—. (2.242)
Теплоотдача при ламинарном пограничном слое. Решением уравнений (2.241) и (2.242) можно определить толщину теплового пограничного слоя 5Т и коэффициент теплоотдачи согласно (2.233). Для этого необходимо знать распределение скорости wx (у) и температуры Ty по толщине теплового пограничного слоя.
Из опыта известно, что распределение в ламинарном потоке имеет параболический характер и может быть удовлетворительно описано уравнением кубической параболы, в которое в качестве неизвестного входит толщина пограничного слоя 6:
— = Иг + ь(4-| • (2.243)
VV0 о о '
Граничные условия:
При у = 0 W = 0;
(2 244)
При у = 5 Wx = WQ.
Уравнение квадратичной параболы неприемлемо, так как не удовлетворяется условие на поверхности: при у = 0 и>Л. = 0 и \>у = 0, так как в непосредственной близости от стенки инерционные силы равны нулю в связи с практически полным торможением потока (условие прилипания). В таком случае из уравнения движения для пограничного слоя (2.239) следует, что этого могло бы не быть, если бы в уравнение параболы входил член (у/5)2. В результате решения уравнения (2.243) совместно с граничными условиями (2.244) получим
Решим вторую часть задачи. Найдем распределение температуры T (у) по толщине теплового пограничного слоя.
Введем новую переменную — избыточную температуру 9 = T — Te и
= T0 — T„ считая температуру стенки Tc постоянной, не зависящей от х. В новом обозначении граничные условия запишутся:
При, = 0 І> = 0;
При у = От & =
В новых обозначениях форма интегрального уравнения энергии (2.241) не изменится
D г5' „ч Л4 . /
Для отыскания распределения температуры по толщине теплового пограничного слоя воспользуемся тем же методом, что и при определении распределения скорости. Вследствие подобия полей скорости и температуры примем параболическое распределение температуры
9 У 1.W3
Вследствие идентичности граничных условий для скорости и избыточной температуры (2.244) и (2.246) получим
З 90 , 1 S0 "=2ЇиЬ-ІГ
Окончательное распределение температуры в тепловом пограничном слое выражается уравнением
Из (2.248) и (2.242) и учитывая, что при у > 5 скорость равна постоянной величине w0 основного потока, а подынтегральное выражение становится равным нулю, получаем выражение для определения толщины пограничного слоя
140
(2.249)
13 w0
Решая последнее, получаем зависимость для толщины слоя
|
5 = 4,64 Х |
|
4,64 1/ЖГХ' |
V*
(2.250)
W о
Или в безразмерном виде
(2.251)
Теперь, подставив полученные выражения скорости (2.245) и температуры (2.248) в (2.241), вычислим интеграл в уравнении теплового потока в пределах теплового пограничного слоя, приняв 8Т ^ 8:
F Twx{h-t)dy= Г Tw,(3o-&)dy = Vv0 Г Tl,5^
|
-dx. |
|
8d8 |
|
(2.248) |
|
0,5 |
|
A v _ _ і 5 JL Оо ' 8Т |
Jo Jo J о L
|
0,5 |
|
Dy = &owoS |
|
1 - 1,5 |
|
28 I 8 |
|
8T |
JWV2 20 [ 8
Считая 8T/8 ^ 1, вторым слагаемым можно пренебречь и считать
»ST „ / с 2
(2.252)
Правую часть уравнения (2.247) найдем из (2.248)
(2.253)
Dyjy=0 ' 8Т
|
А, (2.254) |
Подставив значение интеграла (2.252) и (2.253) в интегральное уравнение теплового пограничного слоя (2.241), получим
З $о 1 / dS 2 dp
|
W* (So - 3) dy = — 90w08 f ^ |
|
J J с |
Или - vv0h3 8 — +2p282 ^
Где Р « 8Т/8.
Подставляя в это уравнение значение толщины пограничного слоя согласно (2.249) и (2.250), получим
|
Р3 + 4х{32 dp |
|
Dx |
|
Р3 + 4хр2 |
14 у 13 а
Подставляя Pr = V/A и считая 14/13 « 1, имеем
_ J_
Dx Рг'
Решением этого уравнения будет
Нгз:(2.255) 5 |/Рг
Показанное ранее соотношение толщин теплового и динамического пограничных слоев получило количественное выражение от Рг. Подставляя значение (2.251) в (2.255), получим окончательное выражение для 8Т:
8, = 4,64 _____ *__ .-. (2.256)
I/Re* ]/Рг
Определим коэффициент теплоотдачи
/ ч Л / Dt
A* (to - fe) = - А, у
А Л, /аэ'
АЛ. Э0 = - X — и а, = - г - —. .
Величина градиента температуры на поверхности пластины легко определяется из уравнения (2.253):
Д§Л _ 3_ 9о_
Ду)у = о 2 8 , ' откуда получаем
А* = - j (2.257)
Подставив 5Т согласно (2.256), получим окончательное уравнение для местного коэффициента теплоотдачи
Ах « 0,331 ~ |/Re^{/Pr, (2.258)
Или
А, = С!ГХ, (2.259)
Где С объединяет величины, не зависящие ОТ X.
Уравнение (2.258) легко привести к безразмерному виду, зная, что Nu* = OlXX/X:
Nu, = 0,331Re°-5Pr°-33. (2.260)
Среднее значение а для пластины длиной / определяется путем формального осреднения местного значения: І і
О о
Где а і — местный коэффициент теплоотдачи на конце пластины длиной /.
177
Согласно (2.261) среднее значение а будет
(2.262)
|
А = 0,662 у }/Re, f/Pr.
|
(2.263)
В формуле (2.263) за определяющую температуру принята средняя температура жидкости, а за определяющий размер — длина пластины вдоль потока. Анализ полученной зависимости для а позволяет выявить роль основных факторов, влияющих на теплообмен.
Как видно из формулы (2.259), коэффициент теплоотдачи уменьшается с увеличением х. Это объясняется тем, что температурный напор £0 — Tc При постоянной температуре поверхности плиты не меняет своего значения, а при увеличивающейся толщине 5х(х) пограничного слоя градиент температуры падает с увеличением х.
Коэффициент теплоотдачи зависит и от направления теплового потока, зависит от того, нагревается жидкость или охлаждается. Градиент температуры в пограничном слое при нагревании больше, чем при охлаждении. Как показывает опыт и анализ влияния градиента температуры в случае нагревания и в случае охлаждения жидкости вдоль пластины, коэффициент теплоотдачи при нагревании капельных жидкостей больше, чем при охлаждении.
По предложению М. А. Михеева, зависимость коэффициента теплоотдачи от направления теплового потока учитывается введением в критериальное уравнение множителя (Ргж/Ргс)0'25, где Prf относится к жидкости при температуре стенки. При нагревании жидкости эта поправка больше единицы, при охлаждении — меньше единицы.
|
|
|
(2.265) |
Окончательное расчетное уравнение теплоотдачи при течении жидкости вдоль плоской поверхности:
(2.264)
Для газов Рг мало зависит от температуры, поэтому формула (2.264) может быть упрощена. Так, для воздуха, приняв Рг = 0,72, получим расчетное уравнение
Nu., = 0,57Re-"f.
Следует отметить, что наличие необогреваемого участка в начале плиты влияет на формирование динамического и теплового пограничных слоев. Это следует учитывать особой поправкой, которая может быть найдена в справочной литературе.
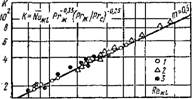
Приведенные зависимости, полученные на основе аналитического решения задачи теплообмена при ламинарном пограничном слое, совпадают с экспериментальными результатами обобщенных данных при постоянных физических свойствах жидкости (рис. 2.33). Такое совпадение свидетельствует о широких возможностях теории пограничного слоя при решении задач конвективного теплообмена. В этом разделе показан путь решения и анализ полученных результатов одной из
простых задач теплообмена. Для более сложных случаев мы ограничимся анализом результатов, полученных опытным путем.
Теплоотдача при турбулентном пограничном слое. Аналитический расчет теплоотдачи в турбулентном слое представляет большие трудности вследствие сложности самого движения и сложности механизма переноса количества движения и теплоты. Особенностью турбулентного течения является пульсационный характер движения. На рис. 2.34 показана осциллограмма колебаний скорости в фиксированной точке турбулентного потока. Отклонение мгновенной скорости w' от средней w называется пульсацией. Наличие пульсаций как бы увеличивает вязкость, и тогда полная вязкость турбулентного потока будет суммой двух величин — молекулярной вязкости и дополнительной турбулентной. Турбулентная вязкость рф не является физическим параметром теплоносителя, как коэффициент динамической вязкости, и характеризует интенсивность переноса количества движения в турбулентном потоке. Аналогично вязкости в уравнении движения, в дифференциальном уравнении энергии дополнительно к молекулярной теплопроводности появляется турбулентная теплопроводность їгр, характеризующая турбулентный перенос теплоты и также не являющаяся физическим параметром теплоносителя.
Аналитическое решение дифференциальных уравнений становится невозможным вследствие трудностей, связанных с определением пульса- циоиных характеристик и их связи с осредненными параметрами потока.
Теоретическое исследование теплоотдачи при турбулентном движении развивается на базе полуэмпирической теории турбулентности Прандтля или на базе гидродинамической теории теплообмена Рейнольдса, основанной на аналогии между процессами турбулентного переноса количества движения и теплоты. Рассмотрение этих вопросов не входит в задачи настоящего курса.
В заключение приведем расчетные формулы, полученные методом гидродинамической аналогии для расчета теплообмена в турбулентном потоке:
Рг
|
1) |
Nux = 0,0296 Re"'8 ---------------------- . (2.266)
І + ^-(Pr W'o
|
4 6 В Ю3 1 ¥ 6 8 10* 2 |
|
Рис. 2.33. Средняя теплоотдача пластин при ламинарном режиме течения: |
|
1 - воздух; 2 — вода; 3 - трансформаторное масло |
W,m/ci .
Рис. 2.34. Изменение скорости в неподвижной точке турбулентного потока
При Рг = 1 формула (2.266) принимает вид
|
(2.267) |
Nu,. = 0,0296 Re°>8
И
Nu, = 0,037 Re°'/8- (2.268)
В этом случае уравнения (2.267) и (2.268) очень хорошо совпадают с результатами эксперимента.
При Рг Ф 1 формула (2.266) должна быть скорректирована. В этом случае рекомендуются эмпирические уравнения:
Nux. = 0,03 Re°-8 Рг£-43 (Ргж/Ргс)0-25; (2.269)
Nu, = 0,037Re°',8 PrЈ43 (Pr3K/Prc)0-25. (2.270)
Для газов среднее значение а по длине пластины I может быть рассчитано по формуле
Шж1 = 0,032 Ре°.Д (2.271)
На рис. 2.35 приведены данные по теплообмену иа поверхности пластины. Критериальные зависимости (2.269) и (2.270) можно решить относительно а, подставив значения критериев. Тогда зависимость коэф-
|
^ЖІ |
J* |
< |
||||||||||||||||||
|
J |
||||||||||||||||||||
|
? |
Й |
|||||||||||||||||||
|
F |
||||||||||||||||||||
|
О - 1 - ® -2 Ф Х ф + -S Ф -7 е -8 ' а -9 ~ Е -10 я -11 « -12 © -13 ® -14 Fa ж І , |
||||||||||||||||||||
|
Т |
||||||||||||||||||||
|
М |
V |
7 / |
||||||||||||||||||
|
А |
/ |
T |
||||||||||||||||||
|
// с® |
'А |
/ |
/ |
|||||||||||||||||
|
'7 2 |
/ / |
|||||||||||||||||||
|
К |
/ // |
|||||||||||||||||||
|
Г |
||||||||||||||||||||
|
2 3 4 5 7 9 10ч 2 3 4 5 Є 8 10* 2 3 4 5 6 в 1Q6 2 3 Рис. 2.35. Местная теплоотдача пластины, омываемой продольным потоком воздуха: I — при ламинарном пограничном слое; II — при турбулентном пограничном слое (м/с): 1 - 260; 2 - 245; 3 - 220 ; 4 - 188; 5 - 162; 6 - 139; 7 - 82,5; 8 - 62,5; 9 - 42,3; 10 - 40,1; 11 - 34,1; 12 - 5,4; 13 - 13,2; 14 - 8,45 |
|
Ном течении жидкости |
Фициента а от определяющего линейного размера выразится формулой а = Сх~0,2, или а = С Г0,2, где С — величина, включающая скорость и физические параметры, не зависящие от х.
На рис. 2.36 приведены результаты обобщения опытных дагщых при турбулентном пограничном слое, полученные М. А. Михеевым. Приведенные формулы действительны при постоянной температуре тепло - обменной поверхности. За расчетную длину пластины / принимают длину обогреваемого участка.
Теплоотдача при вынужденном течении жидкости в трубах. Расчет теплоотдачи при движении жидкости в трубах представляет особый интерес, так как трубчатые аппараты и теплообменники нашли самое широкое распространение на химических производствах.
Течение жидкости в трубах отличается рядом особенностей. Понятия гидродинамического и теплового пограничного слоев в том смысле, в каком они были использованы для расчета теплообмена при плоском течении, сохраняют силу лишь для начального участка трубы, пока пограничные слои, утолщаясь по течению, не сомкнутся, заполняя поперечное сечение трубы. Начиная с этого момента влияние трения распространяется на все поле движения. Различают два режима движения в трубах — ламинарный и турбулентный. Критическое значение числа Рейнольдса ReKp = 2300. В чисто ламинарной области течения при
скоростях, соответствующих значению критического числа Рейнольдса Re < 2300, теплота передается только путем теплопроводности, перпендикулярно направлению течения. С ростом скорости ламинарное движение все более разрушается. При Re ^ 10000 устанавливается устойчивый турбулентный режим. Возникает перемешивание, интенсифицирующее конвективный теплообмен. Теплота передается теплопроводностью лишь в очень тонком ламинарном подслое, откуда она передается в глубь потока движущимися частицами жидкости, называемыми турбулентными полями. При увеличении скорости интенсивность турбулентного перемешивания растет, что ведет к уменьшению толщины пограничного слоя. При этом снижается термическое сопротивление пограничного слоя, что также ведет к интенсификации теплообмена.
Режим течения, соответствующий значениям критерия Рейнольдса 2300 < Re < 1 • 104, называется переходным. В этом случае в потоке могут сосуществовать ламинарная и турбулентная области.
При ламинарном изотермическом течении жидкости внутри технически гладкой трубы устанавливается параболический профиль скоростей. При турбулентном потоке распределение скорости по поперечному сечению имеет иной характер. Максимальный градиент скорости относится к ламинарному подслою, а в ядре потока эпюра скоростей имеет пологий характер усеченной параболы (рис. 2.37).
Как в случае ламинарного, так и в случае турбулентного движения стабилизация потока с характерным для этих режимов распределением скоростей по сечению наступает не сразу при входе потока в трубу. Во входном сечении трубы профиль скорости плоский, а эпюра имеет вид прямоугольника. Под действием сил трения образуется ламинарный пограничный слой, толщина которого растет по мере удаления от входного сечения и затем пограничные слои сливаются. При турбулентном режиме течения, при скоростях, соответствующих Re > 1 • 104, ламинарный слой разрушается и переходит в турбулентный пограничный слой с ламинарным подслоем. После смыкания пограничных слоев течение приобретает стабилизированный турбулентный характер (рис. 2.38). Начальный участок трубы, на котором устанавливается стаби-
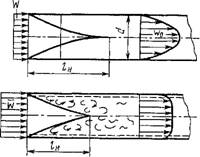
|
Re <2300 |
|
Re У 10 |
|
Рис. 2.38. Влияние начального участка трубы на образование пограничного слоя при ламинарном и турбулентном режимах течения |
|
|
|
Re<r2-W3 |
|
|
|
-Wo- |
|
2QU |
Re>10q
Рис. 2.37. Распределение скорости в трубе при ламинарном (Re < 2 • 103) и турбулентном (Re > 104) течении жидкости
Лизироваиное распределение скоростей, называется участком гидродинамической стабилизации 1И. Длина этого участка для ламинарного потока практически не зависит от Re и равна /„« 15 D.
Аналогично начальному участку гидродинамической стабилизации существует начальный участок тепловой стабилизации /нт. Качественный характер деформации эпюры температур на начальном участке тепловой стабилизации показан на рис. 2.39. Коэффициент теплоотдачи на начальных участках трубы уменьшается, так как вследствие увеличения толщины пограничного слоя растет его термическое сопротивление и падает градиент температуры. При турбулентном режиме течения ламинарный пограничный слой разрушается и коэффициент теплоотдачи увеличивается, затем стабилизируется при установившемся турбулентном режиме (рис. 2.40). На участках тепловой стабилизации коэффициент теплоотдачи принимает постоянное значение. Длина участка тепловой стабилизации при постоянной температуре стенки, при постоянных физических параметрах жидкости, при ламинарном режиме движения равна /,|Т = 0,055 Ре и при турбулентном режиме /нх = 50 D.
Аналитическое решение задач при ламинарном и турбулентном стабилизированном течении связано с решением системы дифференциальных уравнений теплообмена. Однако строгое решение этих уравнений связано с большими математическими трудностями даже для ламинарного течения. Результаты достаточно высокой точности удается получить благодаря обобщению большого числа экспериментов с использованием методов теории подобия.
При ламинарном ре ж и м е течения жидкости теплота передается теплопроводностью по нормали к общему направлению движения потока. Конвективная составляющая теплоотдачи будет больше или меньше в соответствии с распределением скоростей по сечению потока. При значительной разности температур в потоке возникает, как следствие, разность плотностей. На вынужденное движение накладывается свободное движение, турбулизирующее поток, и теплообмен интенсифицируется. Влияние свободной конвекции заметно при Gr • Рг > 8 • 105.
|
Рис. 2.40. Изменение локального коэффициента теплоотдачи по длине трубы при турбулентном течении жидкости |
|
Рис. 2.39. Начальный участок тепловой Стабилизации |
|
I/d ^ so |
Or'1
В этом случае средний коэффициент теплоотдачи рассчитывается по формуле
- 0,15 Re°;33 Pr°-33 (GrJK^Pr„c)0,1 ■ (Ргж/Ргс)°-2Ч (2.72)
За определяющую температуру принята средняя температура жидкости в трубе. Определяющий размер — внутренний диаметр трубы. Если труба не круглого сечения, то за определяющий размер принимается эквивалентный диаметр D3KB — (4F)/P, где F — живое сечение потока; Р — смачиваемый периметр. Например, для канала прямоугольного сечения а х fo:
D3KB = 4afo/[2 (А + fo)] = 2Ab/{A + fo). (2.273)
Для случая а <§; fo эквивалентный диаметр Dim — 2а. В числе Грасгофа Gr = рG&Dz/V2 разность температур $ = tc — ?ж, где T.M — средняя температура жидкости. Множитель (Ргж/Ргс)0,25 отражает влияние направления теплового потока. При нагревании теплоотдача выше, чем при охлаждении. В стабилизированной области (L/D ^ 50) поправка є, = 1. Поправка Е, на нестабилизированном начальном участке потока (L/D < 50) зависит от отношения L/D:
L/d.............................................. 1 2 5 10 15 20 30 40 50
Є,................................................ 1,90 1,70 1,44 1,28 1,18 1,13 1,05 1,02 1
Для воздуха формула (2.272) упрощается и принимает вид
ШЖІІ = 0,13 Re®;33 Gr®;,1 (2.274)
Влияние свободной конвекции с увеличением числа Gr видно из рис. 2.41, где
Ко = Рг. о.43 (рг j'pre)0,25 = 0,15 Re°;33 Gr^. (2.275)
В том случае, когда влиянием свободной конвекции можно пренеб-
|
Рис. 2.41. Средняя теплоотдача при ламинарном и переходном режимах течения жидкости в трубе |
Речь (или она отсутствует, например, в условиях невесомости), средний коэффициент теплоотдачи снижается. При вязком течении средний коэффициент теплоотдачи может быть определен по уравнению
1,55 ^Ре (2-276)
Эта формула действительна при ( 4-) < 0,01 и 0,02 < — ^ 1500.
V Ре d ) цж
За определяющую принята температура T — Tc — 0,5 Д? ср, где ATcp = = (АҐ — Ar")/ln (At'/At") — средиелогарифмический температурный напор; рассчитывается в соответствии с температурными графиками (рис. 2.42, а, б).
При стабилизированном турбулентном движении благодаря интенсивному перемешиванию температура ядра потока практически остается постоянной. Основной градиент температуры относится к пограничному слою. Для расчета среднего по длине трубы коэффициента теплоотдачи можно рекомендовать уравнение М. А. Михеева:
= 0,021 Re^8 Рг0-43 (Ргж/Ргс)°'25єг. (2.277)
Это уравнение справедливо для жидкостей при значениях числа Рг в пределах 0,6 ^ Рг ^ 2500. Для воздуха и двухатомных газов формула (2.277) принимает следующий вид:
Nu =0,018Re°;,8e,. (2.278)
Погрешность расчета по этому уравнению составляет ±5%, если плотность теплового потока на поверхности теплообмена Q < 1 • 105 Вт/м2.
За определяющую в формуле (2.277) принята средняя температура потока T.M = 0,5 (4 + T'.^). Средняя температура греющей стенки для
1 І
Определения Ргс определяется из соотношения Tc = — j0 Tc dx. Для каналов кольцевого поперечного сечения формула (2.277) справедлива для D2/Dx = 1...5.
Поправочный коэффициент єг для коротких труб с нестабилизи - рованным течением (//</ < 50) может быть выбран по табл. 2.1.
|
Т а б л и ц а 2.1
|
A, w
Как следует из формулы (2.278), а = -^g - -2. Коэффициент теплоотдачи увеличивается с увеличением скорости и с уменьшением диаметра трубы.
При движении жидкости в изогнутых трубах и змеевиках под действием центробежной силы возникает вторичная циркуляция. При уменьшении радиуса кривизны влияние центробежного эффекта увеличивается.
При движении жидкости в области развитой турбулентности коэффициент теплоотдачи для изогнутых труб аиз определяется по формуле
Аиз = EDct, (2.279)
Где а — коэффициент теплоотдачи в прямой трубе по формуле (2.277). Поправочный коэффициент єд определяется по формуле
£0=1 + 3,6 (D/D). (2.280)
В области переходного режима 2300 < Re < і • 10* большое влияние на теплообмен оказывает, как и при ламинарном движении, свободная конвекция. В настоящее время не имеется достаточно удовлетворительных методик расчета теплоотдачи в переходном режиме. Приближенно коэффициент теплоотдачи в этой области может быть оценен по данным рис. 2.42. Максимальное значение а соответствует турбулентному течению [уравнение (2.277)], наименьшее значение а может быть рассчитано по уравнению (2.272).
Теплоотдача при поперечном обтекании труб. В химической технологии большое распространение получили трубчатые теплообменники с перекрестным током. Трубы в этом случае обтекаются снаружи перпендикулярным их оси потоком жидкости. Турбулентность потока при этом повышается, что при одинаковых скоростях ведет к повышению теплоотдачи на внешней поверхности труб при поперечном обтекании по сравнению с продольным.
При поперечном обтекании одиночной трубы пограничный слой имеет наименьшую толщину в лобовой части трубы и нарастает, начиная от точки раздвоения потока к миделевому сечению (ср = 90°). Безотрывное плавное обтекание труб имеет место лишь при малых числах Рейнольдса порядка Re яа 5. При больших значениях имеет место отрыв струи и в кормовой части трубы образуется вихревая зона (рис. 2.43, а-в).
В кормовой части трубы (при ср > 90°) скорость снижается вместе с повышением (восстановлением) статического давления, под действием которого возникают возвратные течения и образуются вихри. Возвратные течения оттесняют пограничный слой, вызывают его обрыв и образование вихрей. На рис. 2.44 показано изменение относительного коэффициента теплоотдачи аф/а по окружности трубы при Re = = 2,19 • 105, где а — средний по окружности- коэффициент теплоотдачи. Коэффициент теплоотдачи с^ имеет максимальное значение там, где пограничный слой тоньше.
Положение точки отрыва струи не является стабильным и зависит от характера движения невозмущенного потока. При Re > 2 • 105 отрыв турбулентного пограничного слоя происходит при ср = 120... 140°. При турбулентном режиме обтекание цилиндра улучшается и теплоотдача увеличивается.
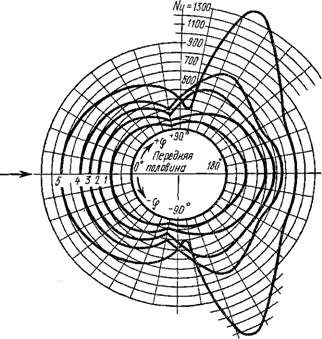
На рис. 2.45 показано распределение местных коэффициентов тепло-
|
Рис. 2.43. Поперечное обтекание цилиндра вязкой жидкостью: безотрывное (а); с отрывом струи (б); с образованием вихревой зоны (в) |
|
90 |
|
W |
|
Рис. 2.44. Изменение относительного коэффициента теплоотдачи при поперечном обтекании трубы |
|
(1) Не =53800 (2) Re =101300 (3) Re —110000 (4)Re =257600 (5) U^mooo |
|
Рис. 2.45. График распределения чисел Nu по поверхности цилиндра |
Рис. 2.42. Температурные графики для расчета среди ел or ар и фм ич е - ского температурного напора при постоянной температуре поверхности нагрева /с в процессе охлаждения (а) и в процессе нагревания (б) жидкости
|
Р |
|||||
|
|
F |
||||
|
V |
|||||
|
U |
|
W вО 120 160 (f>} град |
Отдачи по поверхности цилиндра при разных числах Рейнольдса. Значение Nu максимально в точке раздвоения потока (лобовая часть) и падает до значений, соответствующих углу отрыва пограничного слоя. Как видно из рисунка, при увеличении Re роль кормовой части трубы в теплообмене возрастает.
Сложный характер теплообмена, связанный со сложным движением жидкости при поперечном обтекании трубы (отрыв струи и образование вихрей), затрудняет теоретическое исследование процесса. Все приведенные ниже результаты получены экспериментальным путем. Экспериментальные результаты отдельных авторов могут совпадать лучше или хуже, но они сохраняют общую типичную картину теплообмена. Средний коэффициент теплоотдачи для случая поперечного обтекания одиночной трубы может быть определен по следующим формулам [4]:
При Re^ = 5... 1 • 103
/Рг °'25
Nu, rf = 0,5 Re.^5 Pr.°-38 p^-j ; (2.281)
При Rexd = 1 • 103...2- 10s
Nu«„ = 0,25 Re°i6 Pr°-38 (-^T-)0'23- (2-282)
Для воздуха и двухатомных газов эти формулы упрощаются: при Re*, = 5...1 • 103
Nu^ = 0,43Re^5; (2.283)
При Кежс1 = 1 ■ 103...2• 105
Тжё = 0,216 ReSi6. (2.284)
За определяющий геометрический размер принят наружный диаметр трубы, скорость отнесена к самому узкому сечению канала, в котором расположена труба.
Приведенные формулы справедливы при поперечном обтекании трубы, когда так называемый «угол атаки» J/ = 90 °С. При |/ < 90° коэффициент теплоотдачи определяется из соотношения
Обф = ЄфСХ, (2.285)
Где а — коэффициент теплоотдачи, найденный по формулам (2.281) — (2.284).
Поправочный коэффициент может быть взят из графика (рис. 2.46). При |/ < 90 величина ц < 1. При уменьшении угла атаки коэффициент теплоотдачи снижается.
Пучок труб. Компоновка труб в пучки или пакеты нашла широкое распространение в тепловой аппаратуре химической технологии. Типичное расположение трубных пучков — шахматное (рис. 2.47, а) и коридорное (рис. 2.47,6). Геометрическими характеристиками пучков яв
ляются относительный поперечный (относительно направления потока) sjd и относительный продольный S2/D шаги труб.
Движение жидкости в пучках при низких числах Re может сохранять ламинарный режим, но это сравнительно редкий случай. Чаще имеет место турбулентное движение. Значение ReKp для пучков обычно принимают ReKp = 1 • 105. При Re < 1 • 105 режим течения смешанный.
Процесс теплоотдачи в пучках осложняется тем, что трубы второго
И последующих рядов лежат в вихревом следе, создаваемом трубами первых рядов. По этой причине коэффициент теплоотдачи пучка труб выше, чем одиночной трубы, Омывание первого ряда труб в шахматных и коридорных пучках одинаково. Характер теплообмена на трубках первого ряда аналогичен изменению местного коэффициента теплоотдачи на поверхности одиночной трубы. Начиная с третьего ряда, режим течения и теплообмен стабилизируются. На рис. 2.48 показано изменение коэффициента теплоотдачи по периметру труб, расположенных в первом (1), втором (2) и последующих (3 — 7) рядах шахматного (рис. 2.48, а) и коридорного (рис. 2.48, б) пучков при смешанном режиме течения.
Рассмотрение кривых а =/(<р) позволяет сделать следующие выводы. Для шахматных пучков всех рядов труб локальные коэффициенты теплоотдачи имеют наибольшее значение при ср = 0. Для коридорных пучков ос,» при <р = 0 больше для первого ряда, а для рядов в глубине пучка (<р « 50°) oty имеет максимальное значение, т. е. там, где струя, движущаяся в пучке, «смывает» пограничный слой, утоньшая его при ударе о поверхность трубы. Теплоотдача труб третьего ряда выше, чем первого и второго рядов.
|
1,0 |
|
) |
||||||
|
0,8 |
|
0,6 |
|
SO |
|
70 |
|
Рис, 2.46. Поправочный коэффициент для а одиночной трубы при разных углах атаки |/ |
|
SO 30 |
|
To F , Град |
На основании исследований теплоотдачи в пучках, проведенных Н, В. Кузнецовым и другими, можно сделать общие выводы. Средняя теплоотдача первого ряда определяется начальной турбулентностью потока. Средняя теплоотдача стабилизируется, начиная с третьего ряда,
Rtf^
|
W |
Г Ф - t—&
-ІУ-4
A_.i—а.. 4—А
|
|
|
А |
|
-е |
|
-е- |
ГІфІІ^Гг-ф.
Рис. 2.47. Шахматная (о) и коридорная (б) компоновки трубных пучков
|
|
|
|
|
ОГу ~аГ 1,6 1,5 |
|
О, |
Рис. 2.48. Изменение относительного коэффициента теплоотдачи по периметру труб коридорного и шахматного пучков труб
Так как первые два ряда являются по существу системой турбулизи - рующих устройств. В глубинных рядах устанавливаются гидродинамика И теплообмен, зависящие от геометрии пучка и числа Re.
Теплоотдача первого ряда составляет 60% от теплоотдачи третьего ряда. Теплоотдача во втором ряду несколько выше и в коридорных пучках составляет 90%, а в шахматных пучках — около 70% от теплоотдачи третьего ряда.
Расчет среднего коэффициента теплоотдачи при 103 ^ Re < 105 рекомендуется вести по следующей эмпирической зависимости:
= cRe^PrЈ33(Pra;/Prc)°'24. (2.286)
Для шахматного пучка с = 0,41, п = 0,6; для коридорного с = 0,26, И = 0,65. Влияние компоновочных характеристик пучка определяется поправочным коэффициентом es, который определяется для шахматного пучка при SI/52 < 2 по формуле &S = {SJS2)L/6 и при Si/S2 > 2 Es — 1,12. Для коридорного пучка є5 = (S2/D)~0,15.
Решение уравнения (2.286) позволяет определить коэффициент теплоотдачи для труб третьего и последующих рядов. Для первого ряда коэффициент теплоотдачи ai = 1 = 0,6а; = 3; для второго ряда шахматного пучка <ун = 2 = 0,70 ai = 3 и коридорного ai = 2 = 0,90 аі = 3. В качестве определяющей температуры принята средняя температура потока жидкости, определяющим размером является наружный диаметр труб пучка. Скорость рассчитывается в самом узком сечении пучка.
Формула (2.236) применима при угле атаки vj/ = 90°, т. е. при чисто поперечном обтекании. В том случае, когда vj/ < 90°, средний коэффициент теплоотдачи определяется по формуле
О^ = єфа, (2.287)
Где а — средний коэффициент теплоотдачи по уравнению (2.286).
Поправочный коэффициент є^ может быть взят из графика (рис. 2.49). Средний коэффициент теплоотдачи для всего пучка определяется по средним коэффициентам теплоотдачи для отдельных рядов:
«- = t Рь ■ (2.288)
I=l i=l
Где N — число рядов в пучке; F{ — поверхность теплообмена І-Го ряда.
При равных поверхностях рядов среднее значение а„ определится как среднее арифметическое
А„ = (oc;=i + аг=2 + (и — 2) а{= 3)/и. (2.289)
Теплоотдача при свободном движении жидкости. При свободной конвекции движение возникает под действием разности плотностей нагретых и холодных масс неравномерно нагретой жидкости. Свободное движение полностью определяется наличием теплообмена. Теплообмен - первичная причина возникновения свободного движения.
Если жидкость находится в поле силы тяжести, то наличие неоднородного поля плотностей вызывает появление результирующих подъемных сил, приводящих жидкость в движение, "которое иногда называют гравитационной свободной конвекцией.
Характер свободного движения вдоль вертикальной нагретой пластины показан на рис. 2.50. Вдоль пластины снизу вверх движется ламинарный слой, толщина которого растет по мере того, как в процесс нагрева вовлекаются все новые частицы жидкости. На некоторой высоте ламинарный слой начинает разрушаться и переходит в турбулентный с ламинарным подслоем. Коэффициент теплоотдачи уменьшается с увеличением толщины ламинарного пограничного слоя и стабилизируется в области турбулентного движения.
|
/// |
V |
|||
|
У* |
|
|
1,0 |
|
90 10 50 30 у, ърад Рис. 2.49. Поправочный коэффициент для а пучка труб при разных углах атаки і|/ |
|
Рис. 2.50. Свободное движение теплоносителя вдоль вертикальной нагретой пластины и изменение локального коэффициента теплоотдачи |
|
Рис. 2.51. Пограничный слой при свободном движении у нагретой вертикальной поверхности |
|
0,8 0,6 |
В том случае, когда размеры теплообменной поверхности сравнительно невелики, настолько, что тепловое возмущение локализуется около этой поверхности, окружающую среду можно считать неподвижной. Распределение скорости и температуры в пограничном слое толщиной 8(х) показано на рис. 2.51.
Распределение скорости по толщине слоя напоминает параболическую эпюру. На поверхности теплообмена и на внешней границе скорость равна нулю. В отличие от вынужденного движения скорость сама является функцией определяющих параметров процесса и не входит в условия однозначности. Температура изменяется в пограничном слое, как и при вынужденном движении, от температуры теплообменной поверхности Tc до температуры гж окружающей среды.
Для аналитического исследования теплоотдачи в условиях свободного движения могут быть использованы методы теории пограничного слоя, применяемые при исследовании теплообмена при вынужденном движении. Однако, как показывает опыт, аналитические решения не всегда совпадают с экспериментальными результатами.
В отличие от вынужденной конвекции, в уравнение движения вместо силы тяжести рд, отнесенной к единице объема, должна быть введена подъемная сила рд|3$.
Определяющим критерием при свободном гравитационном движении является критерий Грасгофа Gr = ((3G&L3)/V2, который был получен выше.
Чаще для характеристики движения и интенсивности теплообмена используют произведение (Gr • Рг). Опыт подтверждает, что этот комплекс однозначно определяет значение числа Nu.
Общее критериальное уравнение теплообмена при свободной конвекции имеет вид
Nu = /(Gr • Pr). (2.290)
Для газов уравнение (2.291) может быть упрощено
Nu = f (Gr). (2.291)
Как было отмечено выше, критериальным уравнениям придается вид степенных функций. В этом случае расчетное уравнение имеет вид [5]
Nu = с (Gr • Рг);;,. (2.292)
На рис. 2.52 показаны результаты обработки экспериментальных данных для горизонтальных и вертикальных проволок и труб, вертикальных стенок, шаров, для капельных жидкостей и газов. Экспериментально установлено существование трех режимов, каждому из которых соответствуют пределы изменения комплекса (Gr • Рг)ш. При достаточно малых значениях произведения (Gr • Рг)ш число Nu перестает от него зависеть.
Для проволок диаметром порядка миллиметра и охлаждаемых на воздухе, как показывает опыт, число Nu принимает постоянное
13 ^ 1 M-C(Gv-Prf 1
•о -Ah Горизонтальные проволока и тру$ы
|
13 |
|
Ф Ф Шары Х а ЬДля капельных жидкостей о + д ф *> газов ( |
|
11 |
+ х Вертикальные » » » ЛА ~ стенки 'n^Px^Jk
11
. П-'Л +
|
£ = h18 |
|
0 |
|
■■■■ .. |
|
П = 0 X —о - '-о - L'^ ❖ -3 |
|
-о - -2 |
|
■н—+- |
|
M |
|
193 |
Iq(Gr-'Pp)
Увеличивается на 30%, если нагретая сторона плиты обращена вверх, и уменьшается на 30%, если горячая сторона обращена вниз.
Теплоотдача при свободном движении жидкости в ограниченном пространстве зависит от формы и размеров пространства, рода жидкости и температурных характеристик поверхностей, ограничивающих пространство. Примером ограниченного пространства могут служить воздушные изоляционные прослойки.
|
(2.293) |
|
9 |
|
Эквивалентная |
На рис. 2.53 показан характер циркуляции в замкнутом ограниченном пространстве вертикальной щели и кольцевом пространстве. Из-за сложности процессов определить коэффициент теплоотдачи обычным путем с учетом особенностей движения не удается. В практических расчетах тепловой поток через прослойки толщиной б рассчитывается по уравнению теплопроводности
Хэ
(tcl - te2),
Где Хэкв — эквивалентная теплопроводность, учитывающая конвективный перенос теплоты; fcl, Tc2 — температуры горячей и холодной поверхностей, разделенных прослойкой, теплопроводность определяется из соотношения
Хжв = еД, (2.294)
Где X — теплопроводность жидкости.
Поправочный коэффициент єк, учитывающий влияние конвекции, является функцией (Gr • Рг) и может быть взят из графика (рис. 2.54). За определяющий размер при этом принята толщина прослойки б, а за определяющую температуру — средняя температура жидкости tf.
Теплоотдача при кипении Однокомпонентних жидкостей. В химической промышленности многие технологические процессы связаны с испарением жидкости: дистилляция, ректификация, выпарка и др. Теплообмен при кипении используется не только в аппаратах, предназначенных для испарения жидкости, но также как интенсивный способ охлаждения поверхности. Коэффициент теплоотдачи при кипении на несколько порядков превышает коэффициент теплоотдачи при конвективном теплообмене с однофазной жидкостью.
|
Рис. 2.53. Характер циркуляции теплоносителя в замкнутом пространстве вертикальной щели и в кольцевом пространстве |
Движущей силой для теплового потока в процессе кипения является температурный напор, равный разности между температурой греющей поверхности и температурой насыщения жидкости при заданном давлении At = Tc — TH. Условием возникновения процесса кипения является перегрев жидкости и наличие центров парообразования. Центрами парообразования могут служить неровности и дефекты поверхности, газ, адсорбированный на поверхности или загрязнения. Установлено, что
4- Плоская газоВая прослойка} горизонтальная Х То жег Вертикальная ■о Цилиндрическая газо8ая прослойка
Цилиндрическая жидкостная прослойка ф ШароЗая газовая прослойка
(Gr-Pr)f
Ї01 I 4 6 Ю5 10* 10Ї Ює 107 ' 10s w9 Ю
|
< |
Рис. 2.54. &к =/ (Gr Рг) при естественной циркуляции в замкнутом пространстве
Кипящая жидкость всегда несколько перегрета и на границе раздела фаз всегда имеется небольшая разность температур. Характерное распределение температуры в кипящей воде при атмосферном давлении показано на рис. 2.55. Максимальный перегрев жидкости имеет место у поверхности нагрева, а температура жидкости ґж превышает температуру пара tH. График приведен для поверхностной плотности теплового потока Q = 22500 Вт/м2.
Перегрев может быть больше при больших плотностях теплового потока и зависит от физических свойств жидкости. В зависимости от плотности теплового потока на поверхности нагрева возникают отдельные пузырьки или образуется паровая пленка.
В первом случае режим кипения называют пузырьковым, во втором — Пленочным.
При пузырьковом кипении теплообменная поверхность омывается жидкостью, пограничный слой которой разрушается образующимися пузырьками пара. Пузырьки пара при достижении определенных размеров отрываются от поверхности и всплывают, увлекая за собой столб перегретой жидкости, турбулизируют жидкость, интенсифицируя теплообмен.
При больших плотностях теплового потока, а также при увеличении температурного напора Дг = Tc — T.M число центров парообразования увеличивается, количество образующихся пузырьков и скорость их образования возрастают настолько, что они не успевают отрываться и, сливаясь, образуют на поверхности сплошную паровую пленку, оттесняющую жидкость от нагретой поверхности. Наступает пленочный режим кипения. Паровая пленка может образоваться при меньших тепловых нагрузках вследствие плохой смачиваемости поверхности нагрева.
Интенсивность теплоотдачи при пленочном режиме на порядок ниже, чем при пузырьковом. Это объясняется большим термическим сопротивлением парового слоя на поверхности теплообмена вследствие низкой теплопроводности пара.
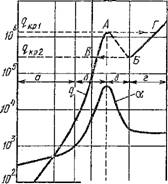
На рис. 2.56 показана зависимость коэффициента теплоотдачи при кипении воды от плотности теплового потока. Верхняя возрастающая ветвь OA соответствует пузырьковому кипению, нижняя ветвь БД — Режиму пленочного кипения. В точке А коэффициент теплоотдачи достигает максимального значения. При дальнейшем увеличении плотности теплового потока пузырьковый режим переходит в пленочный и коэффициент теплоотдачи резко падает до значений в области точки Г. На участке АБ режим кипения называют переходным, в этом случае могут сосуществовать пузырьковый и пленочный режимы кипения. Однако при фиксированном тепловом потоке переходный режим неустойчив и стационарно существовать не может.
Возврат от пленочного кипения к пузырьковому происходит при значительно меньших тепловых потоках (точка Б).
Таким образом, опыт показал существование определенного гистерезиса при переходе от пленочного кипения к пузырьковому.
Изменение температурного напора At = Tc — Tn в условиях фиксированного теплового потока (например, электрообогрев или излучение) показано на рис. 2.57 для кипения воды в большом объеме при нор-
СМодная /поверхность Поды
|
О |
Пар
О 1 г 5 Ь 5 Б 7 8 Расстояние от поверхности нсггреВа, см
|
T 109 108 107 106 105 № ЮЗ M 101 100 |
Рис. 2.55. Распределение температуры в кипящей воде при атмосферном давлении
|
А |
||||||||
|
Jv |
»> |
|||||||
|
/с. |
||||||||
|
Ь® I„ „ |
||||||||
|
Jb®1 |
[ |
|||||||
|
( вс |
Г |
+Д |
|
30 24 18 12 |
|
2 4 & 8 10 12 Q,'105f Вт/м" |
|
Рис. 2.56. Зависимость коэффициента теплоотдачи при кипении воды в большом объеме от плотности теплового потока |
Мальном давлении. Нагрев воды до начала кипения протекает при естественной конвекции (рис. 2.57, а). При At > 5 °С число действующих центров парообразования становится достаточным для начала развитого пузырькового кипения (рис. 2.57, б). Переход (рис. 2.57, в) пузырькового режима в пленочный (рис. 2.57, г) наступает при At = 25 °С (точка А). Стрелкой показано направление кризисного перехода («перескока») от пузырькового кипения к пленочному при постоянном Q (ЛГ). В практическом отношении перерождение пузырькового кипения в пленочное крайне нежелательно. При пленочном кипении температурный напор At = Tc — Tn резко возрастает и в соответствии с Q = A At коэффициент теплоотдачи падает. Температурный напор при пленочном кипении может достичь значений порядка сотен градусов. Температура поверхности может возрасти настолько, что наступает пережог металлической стенки и ее разрушение.
При снижении Q за пределы точки Б происходит переход («перескок») пленочного режима в пузырьковый. Эти «перескоки» можно избежать и сделать переходный режим устойчивым, если задавать не тепловую нагрузку, а тепловой напор At = Tc — TH. Тогда любую точку переходного режима можно реализовать при обогреве поверхности, например, конденсирующимся паром. Тепловой поток при этом будет уменьшаться по мере ухудшения условий теплообмена (участок АБ графика).
Изменение механизма теплоотдачи при переходе от пузырькового кипения к пленочному или от пленочного к пузырьковому называют кризисами кипения, а параметры, им соответствующие, — критическими. Максимальная плотность теплового потока в точке А называется первой критической плотностью теплового потока дкрЬ а минимальная плотность теплового потока при пленочном режиме кипения, соответствую
щая его переходу к пузырьковому кипению, — второй критической плотностью теплового потока с/кр2 = 2 ■ 105 Вт/м2 (рис. 2.56, 2.57).
Такой же характер механизм кипения имеет и для других жидкостей, кипящих в большом объеме на металлических поверхностях нагрева. Значения критических параметров зависят от физической природы кипящей жидкости. Например, для воды QKP, = 8,5 • Ю5 Вт/м2, для этилового спирта <7кР і = 0,6 • 106 Вт/м2, для бензола </нр і = 0,44-106 Вт/м2, для н-гептана QKp[ = 0,356 • 10й Вт/м2.
Теплообмен в режиме пузырькового кипения отличается наивысшей интенсивностью и находит широкое практическое использование.
Как видно из изложенного, процесс кипения жидкости на поверхности теплообмена отличается большой сложностью. Гидродинамические условия процесса определяются характеристиками возникновения роста и отрыва пузырьков пара. К таким характеристикам относят минимальный или критический радиус возникающего на поверхности нагрева парового пузырька RKp, отрывной диаметр пузырька D0 и среднюю скорость роста парового пузырька на поверхности нагрева w = D0F(М/с). Величина /(1 /с) соответствует частоте отрыва паровых пузырьков и определяется как
/=!/( хр + то), (2.295)
Где тр — время роста пузырька на поверхности жидкости; т0 — время омывания поверхности жидкостью между отрывом одного пузырька
И зарождением нового.
Установлено, что пар внутри пузырька испытывает не только давление жидкости, но и сжимающее действие поверхностного натяжения. Для сферической поверхности раздела фаз давление внутри парового пузырька определяется известным уравнением Лапласа
Рп = Рж + 2сг/Якр, (2.296)
|
(l18mjMi А} Вт/(м2-к) |
0,1 1 10 Мкр Юг 10S At,°С
Рис. 2.57. Зависимость плотности теплового потока Q и коэффициента теплоотдачи а от температурного напора At = Tc - r„
|
Рис. 2.58. Схема зарождения паровых пузырей в микротрещине |
Или
Ар = 2a/RKp, (2.297)
Где с — поверхностное натяжение.
При Ар ^ 2ст/Лкр паровой пузырек растет, а при Ар < 2<J/RKp — конденсируется и исчезает.
Чтобы вывести систему из равновесия в сторону роста пузырька, необходимо уменьшить давление в жидкости или увеличить ее перегрев. Если перегрев больше величины, соответствующей RKР, то начинается непрерывный рост паровых пузырьков до размеров, при которых они отрываются от поверхности (рис. 2.58).
С увеличением перегрева количество активных центров парообразования возрастает, так как вступают в действие микровпадины меньших размеров, соответствующих меньшим RKp.
Количественное соотношение между перегревом и RK Р получим из уравнения Лапласа (2.298) и уравнения Клапейрона — Клаузиуса
Г ' ~ 1 (2.298)
ДТ)п Та 1/р„ - 1/р„
Заменим производную конечными разностями. Получим Ар г F 1
(2.299)
АГ Т„ 1/р„ - 1/р,
Учитывая, что р„ <§; рж, получим
Ар = (2.300) Тк
Приравняем Ар [уравнения (2.297) и (2.300)] и получим окончательное выражение критического перегрева
28 Г
А* = U - *« = —• (2.301)
ГРЛкр
Из уравнения следует, что чем больше перегрев, тем больше активных центров парообразования, так как тем меньшего размера RKp микровпадины поверхности становятся действующими. На гладкой чистой поверхности (например, стекло) кипение может наступить при очень больших перегревах — порядка десятков градусов.
Среднее число действующих центров парообразования при заданном перегреве At определяется кроме рельефа поверхности ее адгезионными характеристиками и смачивающей способностью жидкости. Смачивающая способность жидкости определяется краевым углом 0. При 0 < 90° (рис. 2.59, а) жидкость смачивает поверхность (например, вода, спирт, ацетон, бензол, керосин), при 0 > 90 (рис. 2.59, б) — не смачивает (ртуть).
Если кипящая жидкость смачивает поверхность, то пузырек пара имеет тонкую ножку и легко отрывается, если жидкость не смачивает поверхность, то пузырек имеет широкое основание и отрыв его от поверхности связан с большими усилиями и его объем с момента отрыва больше, чем для смачивающей жидкости.
Ъ) Рост парового пузырька на
" " поверхности теплообмена проис
Ходит до определенного размера, при котором он отрывается от поверхности. Отрывной диаметр пузырька D о (м) достаточно удовлетворительно определяется формулой Do = 0,020, где 0 выражается в градусах.
Всплывающие пузырьки обычно не сферические, но за характеристический размер для удобства выбран диаметр сферы, имеющей тот же объем, что и действительный пузырек пара в момент отрыва от поверхности.
Произведение Dо на частоту отрыва пузырьков от поверхности / (2.295) называется скоростью роста пузырьков.
|
А) |
![]()
![]()
|
9. |
|
ШШШШР, ШШШШ7/, |
|
Рис. 2.59, Краевой угол 8 для смачивающих (а) и несмачиваю щих (б) жидкостей |
Если предположить, что скорость роста тр пузырька равна скорости его всплытия т0 в большом объеме, то для этой области кипения при Тр = То имеем
|
0,25 |
|
VQ (Р>, |
|
Ря) |
W = Daf= 0,59
Скорость роста (всплытия) пузырьков зависит от подъемной силы д{рж — Рм), поверхностного натяжения ст и плотности жидкости рж.
Как показывает опыт, скорость роста не зависит от материала поверхности, вязкости жидкости, тепловой нагрузки поверхности и уменьшается с ростом давления (за счет уменьшения D0).
При отсутствии экспериментальных данных для жидкостей скорость роста пузырьков может быть определена по формуле
W = 0,36- 10-3я-1,4 (2.302)
При тс = 0,1...0,4, где я = Р/Ркр — приведенное давление.
Интенсивность парообразования при кипении определяется из уравнения теплового баланса
КИП RpnF Rpn '
(2.303)
Как показывает опыт, действительная скорость пара w несколько выше, чем WK-ип и скорость всплытия отдельных пузырьков Dof. Обозначая согласно (2.303) W = QKp/Rpn, может быть определена первая критическая плотность теплового потока Qm. Коэффициент теплоотдачи при кипении выражается как
А = Q/(Tc - TH). (2.304)
Ввиду сложного характера пузырькового кипения в настоящее время не существует строгой количественной теории теплообмена при кипении.
В специальной литературе описан ряд подходов к оценке эффективности теплообмена при кипении жидкости, основанных на критериаль
ной обработке экспериментальных результатов. В качестве примера приведем некоторые из расчетных формул. Формула, предложенная Д. А. Лабунцовым:
Nu, K = cRe'-Pr1^3, (2.305)
XT al о та
Где Nu = -—, Re =------------- , Pr = —, а постоянные с и N равны: при
Л-ж V5K йж
Re < 0,01 с = 0,0625; п = 0,5; при Re > 0,01 с = 0,125; п = 0,65.
В качестве определяющего размера принята величина I =
= ]А/[> (Рж — Рп)]> пропорциональная отрывному диаметру парового пузырька, a wKIm определяется формулой (2.303). Физические параметры определяются при температуре насыщения. Формула, предложенная Г. Н. Кружилиным:
Nu — 0,082Рг~°'45ІС<І0,7.КІУ3> (2.306)
Q.P-J2 Рж — Рп ~ ~
Где Kq = -І---------------------- — критерии, определяемый числом действующих
Центров парообразования; Ки = —-------------------- —------ критерий, опреде-
Фж« Рп Рж - Рп
Ляемый частотой отрыва пузырьков; / _ ..
9 (Рж ~ Рп)
В. И. Толубинский предложил достаточно простую и физически обоснованную эмпирическую зависимость вида
Nu = 54К°'6Рг0'3, (2.307)
Где К = ^ — критерий кипения, представляющий собой отношение скорости кипения к скорости роста пузырьков. В качестве определяю-
Щего размера принята величина 1 = / ———г-.
/ У (Рж Рп/
Имеются и другие формулы, которые приводятся в специальной литературе, отечественной и зарубежной.
Трудности практического использования критериальных формул связаны в основном с отсутствием опытных данных о теплофизи - ческих свойствах многих веществ.
Как показал опыт, коэффициент теплоотдачи при развитом пузырьковом кипении воды зависит только от плотности теплового потока и давления насыщения. Для этого случая в диапазоне давлений (1 ...40)-105 Па могут быть рекомендованы расчетные уравнения М. А. Михеева:
А = 3,14<2°'7JP0,15; (2.308)
А = 33,4 Af2,33P0,5. (2.309)
При вынужденном течении кипящей жидкости в трубах интенсивность теплоотдачи зависит от соотношения турбулентных возмущений, вызываемых процессом парообразования и самим движением жидкости.
При небольших скоростях потока и при достаточно большой плотности теплового потока теплоотдача определяется процессом парообразования. При больших скоростях движения жидкости теплообмен определяется законами турбулентного движения а ~ vv0,8. С. С. Кутате - ладзе предложен простой и эффективный метод учета совместного влияния скорости циркуляции и плотности теплового потока на теплоотдачу при кипении. В этом случае влияние этих факторов оценивается соотношением предельных значений — коэффициента теплоотдачи при кипении а0о и коэффициента теплоотдачи к вынужденному потоку при отсутствии кипения а0. При а0о/«о < 0,5 принимают а = «о; при аоо/а-о > 2 а = а00- В области 0,5 < а.00/а0 < 2 коэффициент теплоотдачи рассчитывается по интерполяционной формуле
А/осо = (4ао + а00)/(5ос0 - а00). (2.310)
|
А. —С |
Для пленочного кипения характерно существование паровой пленки, покрывающей поверхность нагрева. Пленочное кипение происходит при большей разности температур между твердой поверхностью и жидкостью. Для воды (и большинства органических жидкостей) при атмосферном давлении этот температурный напор составляет > 100°. Пленочное кипение наблюдается в быстродействующих перегонных аппаратах, при кипении криогенных жидкостей, охлаждении двигателей на химическом топливе, охлаждении реакторов и др. При высоких давлениях коэффициент теплоотдачи при. пленочном кипении может так возрасти, что пережога поверхности нагрева не наступает. При высоких температурах при пленочном кипении значительное количество теплоты передается излучением, поэтому коэффициент теплоотдачи при пленочном кипении зависит от излучательных свойств поверхности теплообмена, поверхности жидкости и самого пара. Расчетные зависимости для коэффициентов теплоотдачи при ламинарном движении паровой пленки могут быть получены теоретическим путем. В развернутой форме эта зависимость имеет вид
^Фп(Рж-Рп)^ (23П)
LnAth ' к '
Где С — постоянный множитель, равный 0,667 в случае вертикальной стенки при неподвижной жидкости и 0,943 — при движении жидкости со скоростью, равной скорости движения пара на границе раздела фаз; для горизонтального цилиндра С = 0,53 и 0,72 соответственно, а вместо H следует подставить D.
|
Рп-+х( 1- р" |
|
5 (2.312) |
При вынужденном движении парожидкостной смеси внутри труб течение пара в пленке обычно турбулентное. В этом случае задача решается с использованием физической модели теплоотдачи однофазной жидкости. Для воды в диапазоне давлений от 4 до 20 МПа может быть рекомендована формула 3. Л. Миропольского:
0,8
1 — 0,11 кж Рп )°'4(1-х°'*) Ри
Рж Рж,
Где апл, х — коэффициент теплоотдачи при кипении в том сечении трубы,
в котором паросодержание равно х; а.„ — коэффициент теплоотдачи, рассчитанный по обычной формуле конвективного теплообмена при турбулентном течении однофазной жидкости при том же массовом расходе. Как видно из приведенной формулы, с ростом паросодер - жаиия х коэффициент теплоотдачи в области пленочного кипения увеличивается, что объясняется увеличением скорости движения смеси, а значит и пара в пленке.
Теплоотдача при конденсации. При соприкосновении пара с поверхностью, температура которой ниже температуры насыщения, пар конденсируется. При конденсации пара выделяется теплота фазового перехода, которая отводится через теплообменную поверхность. В зависимости от состояния поверхности конденсат образует на ней сплошную устойчивую пленку. Такая конденсация называется пленочной. Пленочная конденсация имеет место, если конденсат обладает способностью смачивать поверхность. Если конденсат не смачивает поверхность, например, в случае загрязнения ее маслом, то поверхность покрывается отдельными каплями конденсата. Такая конденсация называется капельной. При капельной конденсации пар непосредственно соприкасается с поверхностью теплообмена.
Пленочная конденсация устанавливается на шероховатых, металлических и покрытых оксидной пленкой поверхностях. Даже загрязненные поверхности под влиянием длительной эксплуатации самоочищаются и становятся смачиваемыми. Поэтому большинство промышленных аппаратов работает в режиме пленочной конденсации.
Коэффициент теплоотдачи при пленочной конденсации ниже, чем при капельной, так как стекающая пленка конденсата имеет большое термическое сопротивление. Исключение составляет пленочная конденсация паров жидких металлов, для которых характерна высокая теплопроводность.
При образовании пленки пар отделен от стенки. Принято считать, что температура поверхности пленки, обращенной к пару, равна температуре насыщения.
На рис. 2.60 показан вертикальный разрез пленки. При конденсации пара на вертикальной стенке толщина стекающей пленки конденсата увеличивается, начиная от поверхности кромки стенки. Режим течения конденсата определяют по числу Рейнольдса: Re = w5/vK, где w — средняя скорость течения пленки в рассматриваемом сечении; 8 — толщина пленки.
|
Рис. 2.60. Течение конденсата на вертикальной пластине; распределение скорости и температуры в сечении пленки конденсата |
Ламинарное течение наблюдается в верхней части пленки, когда толщина пленки и количество конденсата невелики. Ламинарное течение пленки может сопровождаться волновым, носящим установившийся периодический характер. При Re > ReKp течение пленки становится турбулентным. Для конденсации неподвижного пара принято считать ReKp = 400.
Взаимосвязь между тепловым потоком и расходом конденсата определяется уравнением
Q = гМ, (2.313)
Где г — теплота конденсации; М — массовый расход конденсата; в сечении / = 8/, М — ржWblz, где L — ширина пленки конденсата.
Вся теплота, выделившаяся при конденсации, отводится через пленку конденсата и по уравнению Ньютона — Рихмана равна
Q = A AtF = а At Xlz. (2.314)
Для ламинарно текущей пленки теплопроводность учитывается лишь в направлении у (рис. 2.60) и при стационарном тепловом режиме уравнение энергии (2.22) приводится к виду
D2T/Dy2 = 0. (2.315)
Уравнение движения (2.29) в этом случае будет
Нж dy2 = Рж9- (2.316)
Левая часть уравнения движения (2.35) равна нулю, так как процесс стационарный и инерционными силами пренебрегаем (vv* вдоль оси х не меняется). Градиент давления Dp/Dx = 0', так как он зависит от гидростатического давления пара вдоль оси х, а оно мало из-за малой плотности пара. Граничные условия:
При у = 0 T = Tc; Vv = 0;
(2 317)
Приу = 5 T=Tn; Dwjc/dy = 0.
Значение производной dvv^/dy = 0 вытекает из предположения, что скорость пара мала и трение на границе пленки конденсата отсутствует.
Интегрирование уравнения энергии с учетом граничных условий дает
Dt/dy = {tH - Tc)/Bx. Коэффициент теплоотдачи определим из уравнений Ньютона и Фурье:
(2.318)
Tn T с Tu Tc Ох
Т. е. коэффициент теплоотдачи обратно пропорционален толщине пленки конденсата и может быть определен, если известно 5Х.
Толщина пленки конденсата 8Х определяется из уравнения движения. Интегрируя уравнение (2.316) при граничных условиях (2.317), получим
W* = ~(2ду - 82). (2.319)
Параболическое распределение скорости показано на рис. 2.60. Средняя скорость течения:
Wx = ±§wxdy. (2.320)
Подставим wx из (2.319), тогда получим
W* = Рж0б2/3цж. (2.321)
Определим массовый расход конденсата через поперечное сечение пленки шириной, равной единице:
= = (2.322)
В сечении, лежащем ниже на величину dx, расход конденсата увеличивается:
DMx = p>Kd (wA • 1) = (2.323)
М'ЯС
Это приращение может быть определено следующим образом. Выразим массу сконденсированного пара через теплоту конденсации г и теплоту, выделившуюся при конденсации:
—а - п
= 5* " ' = ^L (2.324)
Г г г
Тогда увеличение расхода жидкости определится просто:
DМх = ~ — (T„ - Te) Dx. (2.325)
Ох г
Приравняв правые части уравнений (2.323) и (2.325), получим
= (іtH - tc) dx. (2.326)
М-ж r
Интегрируя это уравнение, получим
9Р%гЪ$
+ с.
4А, ж|дж (T„ Tc)
Постоянная с = 0, так как при х = 0 толщина пленки 5 = 0. Окончательное выражение:
|
X |
4 ___________________
4ржА. ж (Tn tc)x 327)
Р 2дг
Значение коэффициента теплоотдачи получим, подставляя (2.327) в формулу (2.318):
4М*н-**)*'
Среднее значение а по поверхности пластины найдем интегриро-
где H — длина участка осреднения. После интегрирования получаем
4
А = 0,943
В критериальном виде формула (2.330) будет
__ ±
Nu = 0,943 (ArPrK)4, (2.331)
Ос/з Gh3 . ,, »*
Где Nu = -—; Аг = —Jjz------------ —число Архимеда; К
К' V2 (1 - р„/рж) " ' (Ср)ж-Аґ
Число фазового перехода.
В том случае, когда р„/рж 1, вместо числа Аг следует пользоваться числом Галилея Ga = Gh3/V2.
Приведенный вывод принадлежит Нуссельту и относится к чисто ламинарному режиму течения пленки. П. Л. Капица показал, что при установившемся волновом движении средняя толщина пленки конденсата меньше, чем при строго ламинарном. Д. А. Лабунцов предложил поправку к (2.330) на волновое течение в виде функции от числа Рейнольдса ^ _ Re0.04 (2 332)
Для чисто ламинарного течения (Re <10) эта поправка близка к единице.
Таким образом, коэффициент теплоотдачи при конденсации чистого неподвижного пара определяется по формуле
А = адгЄиЄ,, (2.333)
Где Oln — коэффициент теплоотдачи по формуле Нуссельта (2.330); є, — коэффициент, учитывающий влияние температуры на физические свойства конденсата и определяемый из зависимости
Є, = (kc/K)3IB (P„/Pc)1/8. (2.334)
Поправка є, справедлива при 0,5 < 1„/Хс < 2 и 0,1 < р„/Рс < 1.
Для наклонных поверхностей вместо д следует ввести проекцию вектора ускорения свободного падения на ось х: дх — д cos Р, где (3 — угол между вектором силы тяжести и направлением движения
Пленки. Тогда для наклонных поверхностей анак = аверт j/cos [і
Полученные результаты применимы также при конденсации на наружных и внутренних поверхностях вертикальных труб, диаметр которых больше толщины пленки конденсата.
|
Ванием (2.328) по высоте H: |
|
А = ~—§Qaxdx, (2.329) |
Для горизонтальной цилиндрической трубы в случае непрерывного стекания конденсата величина (3 переменна. Для этого случая Нуссельт получил среднее значение коэффициента теплоотдачи на одиночной горизонтальной трубе в виде
а = 0,7251/ —<2"335) І Р. ж Tn TcJ И
За определяющий размер в этом случае принят наружный диаметр трубы D.
Для горизонтальных пучков коэф
Фициент теплоотдачи меньше, чем для одиночной трубы, и рассчитывается по формуле
О&пуч —~
Поправка ez берется по графику рис. 2.61 и зависит от расположения труб в пучке и числа рядов z. На рисунке кривая 1 для шахматного, кривая 2 для коридорного расположения труб. Уменьшение а в пучках связано с увеличением толщины пленки на трубах, расположенных в нижних рядах, где накапливается стекающий конденсат.
На вертикальных трубах для отвода конденсата с целью уменьшения толщины пленки устанавливаются специальные копденсато - отводиые колпачки.
При конденсации перегретого пара следует учитывать теплоту перегрева с]пп и вместо теплоты конденсации в расчет вводить сумму Г + с/,,,,, где <у,|П = //„„ — H", а Him и И" — энтальпии перегретого и насыщенного паров. Обычно перегрев незначительно меняет а и во многих случаях теплотой перегрева можно пренебречь.
Содержание в паре неконденсирующихся газов существенно снижает коэффициент теплоотдачи. Так, содержание 1 % воздуха в водяном паре снижает коэффициент теплоотдачи на 55...60%, а 2 % — почти в три раза. Это уменьшение а объясняется накоплением у стенки неконденсирующихся газов, чему способствует снижение парциального давления пара в парогазовой смеси. Пограничный слой с неконденсирующимся газом создает дополнительное термическое сопротивление.
Температурный напор At = f„ — fc в этом случае также снижается, так как снижается температура насыщения, соответствующая парциальному давлению пара.
В промышленных конденсационных установках воздух из пара удаляется специальными воздушными насосами.

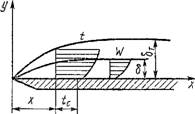
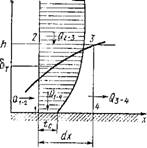
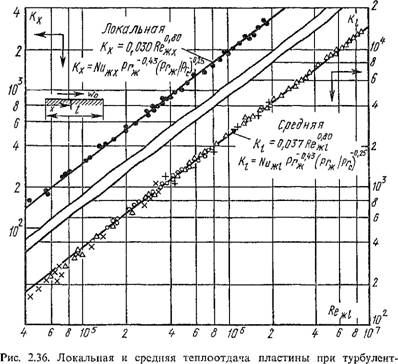
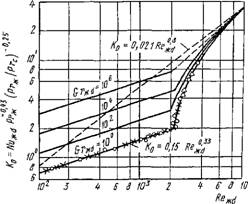
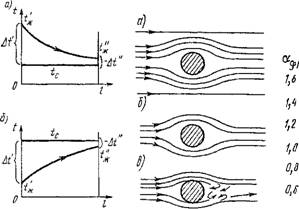
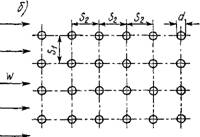
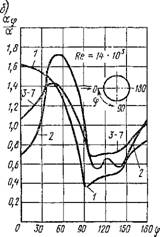
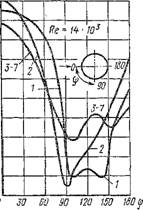
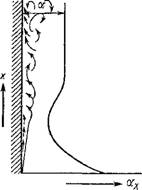
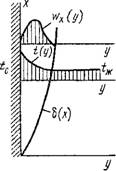

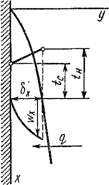
 Опубликовано в
Опубликовано в