Простейшим методом термодинамического анализа ЭХТС является энергетический, основанный на первом законе термодинамики. Этот метод позволяет оценить потери энергии в ЭХТС и в ее отдельных элементах, а также выявить элементы ЭХТС, процессы в которых протекают с наибольшими потерями. Существенным недостатком этого метода является то, что в нем не учитывается ценность различных видов энергии, т. е. их практическая пригодность, что неверно с точки зрения второго закона термодинамики. Как было указано выше, в реально протекающих процессах происходят потери энергии на необратимость. Поэтому в настоящее время приме­няются два метода термодинамического анализа систем, учитываю­щих необратимость термодинамических процессов: энтропийный (метод циклов) и эКсергетический. Оба метода были обоснованы в работах Р. К. Клаузиуса, Д. В. Гиббса и А. Стодолы. Существенный вклад в развитие и использование этих методов внесли советские ученые А. И. Андрющенко, В. М. Бродянский, Д. П. Гохштейн и др. Оба метода основаны на втором законе термодинамики и по существу решают одну и ту же задачу определения потерь работо­способности, потерь на необратимость реально протекающих процессов. Однако на базе эксергетического метода можно более тщательно провести термодинамический анализ ЭХТС и изыскать наиболее эффективные пути уменьшения затрат топливно-энергетических ресур­сов при одновременном повышении технологических показателей.

Энтропийный метод. Энтропийный метод термодинамического ана­лиза систем позволяет на базе первого и второго законов термо­динамики найти связь между внешними энергетическими потоками (количеством теплоты и работы) и параметрами системы, а также между некоторыми внутренними параметрами. Посредством анализа теплового баланса системы, в которой совершаются термодинами­ческие процессы, можно вычислить характеризующие их коэффи­циенты и сопоставить их с аналогичными коэффициентами идеальных термодинамических процессов. Это позволяет определить в данной системе суммарную потерю производимой и затрачиваемой работы вследствие необратимости процессов. Если для инженерного анализа системы этих данных недостаточно, то анализ циклов дополняется подсчетом возрастания энтропии в отдельных частях системы.

Для термодинамической оценки эффективности системы (данной установки) следует ответить на четыре вопроса, а именно: 1) насколь­ко велик к. п. д. обратимого цикла установки, от каких факторов он зависит и что следует предпринять для его увеличения; 2) насколько велики потери от необратимости в реальной установке; 3) как распре­деляются эти потери по отдельным элементам установки; 4) на усовершенствование какой части установки следует обратить внимание с целью уменьшения степени необратимости, в частности увеличения к. п. д. цикла, по которому работает установка. В соответствии с этими задачами термодинамический анализ установки проводится в два этапа: вначале анализируется обратимый цикл, а затем необратимый с учетом основных источников необратимости. В дальнейшем к. п. д. об­ратимого цикла

T|t _ - iiL= і _ Si.» IlL (1.208)

Ч Ч Чі

Будем называть термическим к. п. д., а реального

= (1.209)

Ч

Внутренним, подчеркивая тем самым, что речь идет о к. п. д. собственно цикла, который характеризует степень совершенства процессов, совер­шаемых рабочим телом.

Известно, что степень совершенства данного обратимого цикла ха­рактеризуется сравнением его термического к. п. д. с термическим к. п. д. цикла Карно в том же интервале температур, т. е. относительным термическим к. п. д.

T|q = ——. (1.210)

Л к

Для того чтобы оценить, насколько данный действительный (необра­тимый) цикл менее совершенен, чем теоретический (обратимый), вводят понятие относительного внутреннего к. п. д. цикла как отношение

11ш = Лі-=|_. (1.211)

Л< 'и

Однако кроме необратимых потерь, учитываемых Ло< (т. е. потерь, имеющих место в процессах, совершаемых собственно рабочим телом в цикле), в реальных условиях работы установки имеются потери, обусловленные необратимостью тепловых, механических, химических и электрических процессов в отдельных узлах ее. Поэтому эффективность реальной установки в целом характеризуется так называемым эффектив­ным к. п. д. Ле> который представляет собой отношение количества энергии (в форме теплоты или работы), отданной внешнему потреби­телю, к количеству энергии (в форме теплоты или работы), подведен­ной к установке. Эффективность системы может быть оценена также работоспособностью ее: подсчитав потерю работоспособности в каждом элементе, можно найти потерю работоспособности всей системы.

Обязательным элементом ее являются устройства, в которых за счет подвода работы извне осуществляются процессы сжатия (компрес­соры, турбокомпрессоры, насосы и т. д.), и устройства, в которых производится работа путем расширения (паровые и газовые тур­бины, турбодетандеры и т. д.). Реальные процессы расширения и сжатия сопровождаются потерями на необратимость и поэтому внут­ренний относительный к. п. д. каждого J-Го элемента системы находится следующим образом:

Для расширительных устройств

Л Kj = (і-212)

Где и LpJ — действительная и теоретическая работы расширения J-Vo элемента системы;

Для сжимающих устройств

Tfou =-т^Ч (1-213)

Где Lcj и — теоретическая и действительная работы сжатия J-Го элемента, которые совершаются за счет подвода энергии извне; здесь в действительном процессе сжатия приходится затрачивать энергию на сжатие (/£,) большую, чем в теоретическом процессе, на величину потерь на необратимость.

Таким образом, в установке обратимая работа цикла

K = Z4j~ Z4j> (1-214)

;= І J=I

А необратимая

'S= Zto - I (1-215)

J=I J=І

Или с учетом формул (1.212) и (1.213)

T^J^J-likjMoiJ - (1-216)

J= І ;= І

Тогда с учетом формулы (1.211) можно написать, что

J = Tl J = п

Е 1Р. А - Е (Hjfaoij) Лої = — —п ^ • <L217)

Е 1Pj - Е

J=i J=I

Внутренний к. п. д. цикла гн с учетом формул (1.208), (1.214) и (1.217);

TOC o "1-3" h z J=n j=n j=n j=n

E 1Рл$і - E Ocjfaou) E 1P.JNfiu - E (Kjmoij J=i j=i ^ j=i j=i

ЛІ = ЛоіПЇ =----------------- ;------------------- - =----------------------------------- •

/д q і

(1.218)

Величина потерь в каждом элементе системы характеризуется еще величиной эффективного к. п. д. этого элемента т}eJ. Перемножив между собой все эффективные к. п. д. элементов системы на абсолютный внутренний к. п. д. цикла, получим эффективный абсолютный к. п. д. для всей системы

J = N

Л С = Л 0І Л Г П reJi (1.219)

J= і

J = n

Где П reJ — произведение величин эффективных к. п. д., характеризую - j= і

Щих необратимые потери во всех п элементах системы.

К. п. д. г)с, показывает, какая доля выделенной в системе теплоты превращена в полезную работу, отданную внешнему потребителю;

*пол = Ле9і. (1.220)

Очевидно,

Ад = (1 - л.) (1-221)

Представляет собой долю теплоты qu не превращенную в работу, и включает в себя как теплоту q2, передаваемую холодному источнику, так и потери теплоты Aqn, обусловленные необратимостью про­цессов в отдельных элементах установки вследствие трения и ко­нечной разности температур, потерями в окружающую среду и т. д. Очевидно,

А <2 п = 1ц 'пол» (1.222)

Где /ц — работа, производимая в обратном цикле.

С учетом формул (1.208) и (1.220) можно написать, что

Aqn = л«<7і - Л,</і = (Л< - Л,)<?ь (1-223)

А так как максимальная обратимая работа цикла может быть получена только в обратимом цикле Карно, то, следовательно, максимальная потеря работоспособности А/„ в системе, равная максимальному зна­чению Aqw будет

А'п = <?i (Л* - Ле). (1-224)

В отличие от энергетических установок в ЭХТС наряду с машинами имеется очень много технологических аппаратов, в которых, как из­вестно, никакой работы не производится. Однако в этих аппаратах имеются большие потери на необратимость: конечная разность темпе­ратур, протекание химической реакции и т. д. В рассматриваемом методе термодинамического анализа они учитываются при определении эффективного к. п. д. Ле анализируемой установки. Однако определение этих потерь связано с большими трудностями и поэтому при термодинамическом анализе ЭХТС методом циклов очень важно оценить эффективность работы всех ее элементов — и машин и технологических аппаратов, подсчитав для каждого из них потерю на необратимость по формуле (1.207).

В соответствии с формулой (1.207) потеря работоспособности ЭХТС

А/^,тс = Т0 ДРХТС.

Изменение энтропии системы равно сумме изменений энтропии огдель ных ее элементов, т. е.

Д, ЭХТС= '^"д,. І-- 1

Умножая на температуру окружающей среды І о, получим

А/эхтс = Т0 As3XTC = T0Ast= Z А/ь (1-225)

1=1 1=1

Т. е. величина потери работоспособности всей системы в целом равна сумме потерь работоспособности в отдельных ее элементах. Найден­ные значения А/г покажут, в каких элементах ЭХТС необратимые процессы вносят основной вклад в величину А/эхтс и, следовательно, какие процессы в этих элементах системы должны быть в первую очередь усовершенствованы.

Эксергетический метод. Эксергетический метод термодинамического анализа ЭХТС основан на широком использовании эксергии. В самом общем смысле эКсергия вещества есть максимальная работа, которую оно может совершить в обратимом процессе с Окружаюіцей средой в качестве источника даровой теплоты, если в конце этого про­цесса все Участвуюіцие в нем виды материи переходят в состояние термодинамического равновесия со всеми компонентами окружающей среды.

Эксергетический метод является универсальным способом термоди­намического исследования различных процессов преобразования энер­гии в ЭХТС. Все реально протекающие процессы — необратимые, и в каждом случае необратимость является причиной снижения совер­шенства процесса. Это происходит не из-за потери энергии, а из-за Понижения ее качества, так как в необратимых процессах энергия не исчезает, а обесценивается. Так, например, дросселирование рабочего тела не изменяет его энергии (Hx — H2), а снижает ее пригодность к совершению работы или использованию в теплообменниках. Таким образом, каждое необратимое явление — это причина безвозвратной потери энергии. Универсальность эксергетического метода термодинами­ческого исследования ЭХТС следует рассматривать в том смысле, что характер процессов анализируемой системы (например, круговой или разомкнутый) не имеет принципиального значения: подход к решению задачи и метод ее решения не изменяются. В эксергетическом ме­тоде термодинамического анализа ЭХТС каждый ее элемент рас­сматривается как самостоятельная термодинамическая система. Эффек­тивность работы каждого элемента ЭХТС оценивается путем сравнения эксергии на входе в этот элемент с потерей в нем работоспособ­ности, т. е. с потерей эксергии в результате необратимых процессов, протекающих в этом элементе, и обусловленных как внутренней (потери на компенсацию в рабочем теле градиентов А р/р, Ар/р и А Т/Т и трение о стенки канала), так и внешней (потери на конечную разность температур при теплообмене) необратимостью. Таким обра­зом, при определении потерь эксергии в каждом элементе исследуемой ЭХТС выявляются и количественно оцениваются причины несовер­шенства протекающих в них процессов, что дает информацию о возможности повышения совершенства во всех элементах и позволяет создать наиболее совершенную ЭХТС. Это является основной целью эксергетического метода анализа ЭХТС.

Виды эксергии. Эксергия делится на два основных вида, а именно: эксергия видов энергии, не характеризуемых энтропией, для которых она равна самой энергии е — Э (механическая, электрическая и др.), и эксергия видов энергии, характеризуемых энтропией е ^ Э (внутрен­няя энергия, энергия излучения, термомеханическая, нулевая). Эксергия последних видов энергии подразделяется на эксергию вещества в замкнутом объеме, эксергию потока вещества и эксергию потока энергии. Эксергия вещества в замкнутом объеме состоит из термо­механической (физической), нулевой (химической — в реакторах периоди­ческого действия) и излучения. Эксергия потока вещества состоит из термомеханической и нулевой. Эксергия потока энергии состоит из эксергии теплового потока и эксергии излучения.

Эксергия вещества в замкнутом объеме е„ рассмат­ривается в закрытых системах. Определим термомеханическую эксер­гию вещества в замкнутом объеме, т. е. максимальную работу, которую может совершить вещество с начальными параметрами Р, V, Т, и, H, S при обратимом переходе в равновесие с окру­жающей средой, когда его параметры будут иметь значения р0, V0, Т0, U0, ho, So - Для того чтобы вещество перешло в равно­весие с окружающей средой, необходимо изменить его внутреннюю энергию за счет подвода (или отвода) к нему теплоты либо за счет совершения им работы, поскольку в соответствии с первым законом термодинамики du = 5q — 8/.

В обратимом процессе подвод теплоты к веществу либо отвод от пего теплоты в окружающую среду происходит при постоянной температуре, равной температуре окружающей среды Т0, т. е. Dq = TQ ds. Тогда эксергия вещества в замкнутом объеме Dev будет равна работе 5/ за вычетом работы, затрачиваемой веществом на преодоление им давления окружающей среды р0 Dv, т. е.

Dev = Ы — р0 Dv = Hq — Du — р0 Dv — TQ Ds — Du — P0 Dv, (1.226) или после интегрирования

Є„ = TQ (SQ - S) - (uQ ~ u) - Po (v0 - V) = (u - UQ) - To (s - So) + Po(v - Do).

(1.227)

Так как для данной среды, окружающей вещество, PQ, V0, Т0, и0 и s0 есть величины постоянные, то уравнение (1.227) можно представить в следующем виде:

Ev = и - T0S + P0V + с, (1.228)

Где с =- и0 + T0S0 - PQV0 — const, и следовательно, е„ является пара­метром состояния вещества и среды — эксергетической функцией.

Для определения термомеханической эксергии потока ве­щества требуется найти максимальную работу его при обратимом переходе от данного состояния, характеризующегося параметрами Р, V, Т, и, H и s, к равновесному состоянию со средой, т. е. с параметрами р0, V0, Т0, щ, H0 и S0. Очевидно, эксергия потока вещества е отличается от эксергии вещества в замкнутом объеме Ev на величину работы, связанной с перемещением потока. Для конечного изменения состояния эта работа будет равна работе Pv За вычетом работы P0V, затрачиваемой на преодоление давления среды,

Pv -P0V = V{P- Ро). Следовательно, эксергия потока вещества

E = Ev + V(P-ро). (1.229)

Подставляя в уравнение (1.229) значение е„ из уравнения (1.228), получим

Е = (и + Pv) - T0s - и0 -h T0S0 + P0v - P0v0 - P0v.

Учитывая, что и + Pv - H, a —U0 + T0SQ - PQv0 = с есть величина постоянная, окончательно получим

Е = H - T0S + с. (1.230)

Функция е, равно как и <?„, является эксергетической функцией, так как ее величина однозначно определяется параметрами вещества и среды.

Обычно в расчетах определяют разность величин Aev и Ае в двух состояниях системы. В этом случае Aev и Ае будут соответственно равны

Aev = Au-T0As + P0Av, (1.231)

Ае = Ah — Т0 As. (1.232)

Следует иметь в виду, что эксергия вещества в замкнутом объеме определяется взаимодействием его с окружающей средой только по температуре и давлению; состав окружающей среды значения не имеет.

Н у л е в а я (х и м и ч е с к а я) э к с е р г и я е0 связана с установлением равенства химических потенциалов между соответствующими компо­нентами вещества и окружающей среды и измеряется количеством работы, которая может быть получена в обратимом процессе установления равновесия компонентов вещества с соответствующими компонентами окружающей среды при р0 и Т0. Следует помнить, что процессы взаимодействия вещества с окружающей средой, связан­ные с обменом массы, не всегда сопровождаются химическими реакциями; примером этого являются процессы разделения, смешения и растворения. В химических реакторах нулевая эксергия является основной. Для определения с о необходимо знать состав окружающей среды. Однако состав окружающей среды весьма неоднороден, и поэтому расчет абсолютных значений eQ с такой же точностью, как расчет е и Ev, принципиально невозможен. Обычно для практи­ческих целей вводят упрощающие допущения в расчете е0, однако при условии соответствия требований эксергетического анализа и строгого термодинамического обоснования.

Вычислим нулевую эксергию при химических превращениях. Пусть в химическом реакторе протекает реакция

+ >2А2 + ...^ \А + V2A'2 + ..., (1.233)

Где vb v2,... и v'x, v2 ... — стехиометрические коэффициенты соот­ветственно исходных Ati А2,••• и получающихся А'ъ А2,.., веществ.

В инженерной практике расчет нулевой эксергии при химических превращениях, протекающих в химических реакторах, ведется на осно­вании формулы эксергии потока вещества е (1.230).

Если реакция протекает при температуре Т = 298 К, то эксергия Ехр (кДж/моль) определится по формуле

Ехр~Аг°298 ~%Е0ф (1.234)

J

Где AZ°298 = ]Гуг(ЛZ°298)I ~ ZvHAZ°298)'I = І>г(ДЯ°98)£ - ЈvJ(A - І і і і

~ ~ ZvK^sX]; А2298 — стандартный изобарно-изотерми-

І і

Ческий потенциал при 7"= 298 К, ' кДж/моль; (АН298)' и (АН29В) - стандартные значения энтальпий (теплоты образования) конечной и начальной составляющих реакций соответственно, кДж/моль; (s298)' и (Агов) — стандартные абсолютные значения энтропии конечной и начальной составляющих реакции соответственно, кДж/(моль-К);

YJEQj — сумма значений нулевых эксергий дополнительных веществ, J

Участвующих в реакции [левая часть уравнения (1.233)], взятых при ро и Т0 (например, в реакции получения СаСОэ по уравнению Са + 0,502 + С02 = СаС03 дополнительными веществами являются 02 и С02).

Методику определения нулевых эксергий дополнительных веществ и таблицы их значений для элементов наиболее распространенных неорганических соединений можно найти в монографии «Эксергия» Я. Шаргута, Р. Петела (М., 1968).

Если реакция протекает при температурах выше 298 К, то с достаточной для инженерных расчетов точностью нулевую эксергию химического превращения в реакторах можно подсчитать по формуле

Ехр = AZ°t-]TЈOj, (1.235)

Где

(

Т 298

2'31g 298~~1+ ~Т~}

А^р.298 = 1>г(цср>298)г - Х>і (ЦСр. гевХ;

І і

(|ісРі298)г и (|xc'p>298X - - мольные изобарные теплоемкости при темпера­туре 298 К начальной и конечной составляющих реакции соот­ветственно, кДжДмоль • К).

При вычислении AZ°T надо брать абсолютное значение величины ДМ<Ср,298-

Если дополнительные вещества в окружающей среде находятся не

В виде соединения с другими веществами, а в свободном состоянии (как, например, газы атмосферного воздуха), то нулевая эксергия J-Ro компонента вещества E0J определяется минимальной работой, необходимой для получения его в чистом виде при параметрах среды Ро и Т0. В этом случае в соответствии с формулой (1.230)

EQj = АН0 + Т0 (S0 — S) = Т0 (S0 - S) = Rj-IjT0 In {P0/Pj (1.236)

Где AH0 = 0 при T0 = const для любого компонента воздуха, рас­сматриваемого как идеальная газовая смесь компонентов; так как парциальное давление /-го компонента этой смеси — Vjp0 = Njp0, где rj и Nj — объемные и мольные доли компонентов в смеси, то окончательно:

E0j = R[ijT0n(l/Nj). (1.237)

В этом случае, например, эксергия потока воздуха (Д/г0 =0): Е = H - T0s + с + е0 = срт(Т - Т0) - - Т0 [cpm In (Т/То) ~ R In (р/ро)} + Z RiT0 In (l/rЈ) = = срт(Т~ То) - Т0 [срш In(T/TQ) ~ R In(Р/Ро) ~ IR; In (l/rdl

Где изменение энтропии As написано в соответствии с формулой (1.83), а г; — объемная доля компонента в воздухе.

Эксергия Eq теплового потока Q рассчитывается по урав­нению

= Ї 8ft - Е ^ (1-238)

1=1 І (=1

Гдете = 1 — (Т0/Т) называется эксергепшческой температурной функцией.

В частном случае при Т = idem и те = 1 — (Т0/Т) — idem формула (1.238) представится в виде

Eq = Qxe. (1.239)

Функция те имеет универсальное значение: она пригодна для оценки максимальной работоспособности в круговых и разомкнутых термо­динамических процессах.

Можно доказать, что частная производная термомеханической эксер­гии потока по энтальпии при постоянном давлении равна т4>, т. е.

(Ј)f-V (1.240)

Так как (8H)P = 8Qp или (Ah)P = Qp, то из уравнений (1.238) и (1.239) следует, что

(Ае)р = (Ah)PXe = Qp т, = (Eq)P, (1.241)

Т. е. изменение эксергии потока рабочего тела в изобарном процессе равно эксергии Eq связанного с этим процессом теплового потока. Следовательно, во всех процессах теплообмена, протекающих при постоянном давлении, эксергию теплового потока можно вычислять

По разности эксергий потока вещества Де. Это значительно упро­щает расчеты, когда точный расчет непосредственно еч является трудоемким, как, например, при переменной температуре.

Эксергия излучения ес определяется максимальной работой, которая может быть совершена в обратимом процессе приведения этого излучеиия в состояние равновесия с окружающей средой (при 7'0). Ее вычисляют по уравнению

, (1.242)

Где є — степень черноты поверхности; С0 — коэффициент лучеиспускания абсолютно черного тела.

Эксергетические диаграммы состояния. Эксергетические диаграммы широко применяются при термодинамическом анализе энерготехноло­гических систем: из них непосредственно определяются величины е, Eq и их составляющие для различных веществ и их смесей, значения те при заданных значениях Т и Т0, а также наглядно и просто проводятся решения соответствующих задач. Среди известных эксер - гетических диаграмм наибольшее распространение получили следующие: Hs- и Ts-диаграммы с линиями е — idem и Eh-Диаграмма. Обозна­чим через Т% — нормальную температуру кипения.

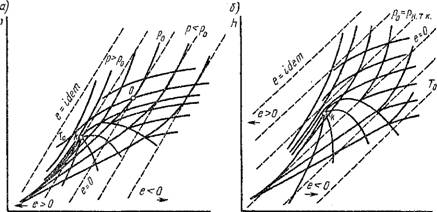
На рис. 1.48 изображены Hs-Диаграммы с нанесенными на них линиями е = idem: А — при Т0 > Т*; б — при TQ = Т*. Точка начала отсчета (нулевое состояние) определяется только параметром Tq И в некоторых случаях р0. Как видно из этой диаграммы, эксергия вещества для данного термодинамического состояния определяется посредством равномерной сетки прямых е — idem. Выше линии е = О расположена область положительных значений эксергии (е> 0), ниже — отрицательных (е < 0).

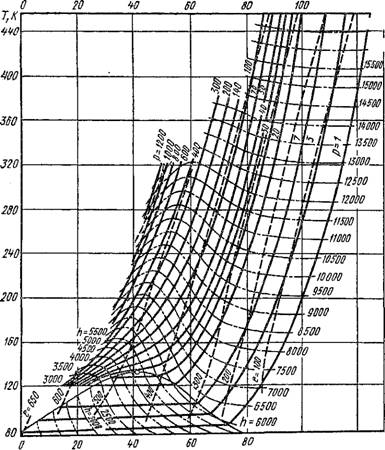
На рис. 1.49 представлена Ts-диаграмма воздуха с нанесенными на ней линиями е = idem, которые, в отличие от предыдущей диаграм-

Рис. 1.48. /Zs-диаграмма паров с нанесенными на ней линиями е = Idem

І

S

S

120 130

Moo

WO 120 W б, КДж!(К моль • к)

Рис. 1.49. ^-диаграмма воздуха с нанесенными на ней линиями е = Idem

Мы, являются неэквидистантными линиями (за исключением области влажного пара).

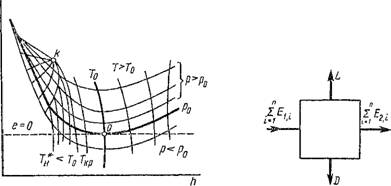
На рис. 1.50 изображена е/г-диаграмма при Т0 > Т*. Нулевая точка определяется пересечением изобары р0 с изотермой Т0, находящейся в области перегретого пара или газа. Если в любой точке пере­сечения изотермы с изобарой провести касательную к последней, то тангенс угла наклона а ее будет численно равен эксергетической температурной функции тс, поскольку в соответствии с формулой (1.240)

При этом возможны три случая: если Т > Т0, то tgap>0 и, 78 следовательно, tL, > 0; если Г < Т0, то tg ар < 0 и хе < 0, если Т — Т0, То tg ар — 0 и х(, = 0.

С помощью ей-диаграммы можно найти работу и другие характе­ристики разомкнутых процессов и циклов.

Эксергетические балансы и эксергетические к. п. д. ЭХТС и ее Отдельных элементов. При исследовании ЭХТС в первую очередь составляются материальный и тепловой балансы, а затем уже эксер - гетический.

Тепловой баланс не отражает степень приближения ЭХТС к идеаль­ной, ее термодинамическое совершенство. В отличие от теплового баланса эксергетический баланс учитывает потери от необратимости в ЭХТС и тем самым отражает степень приближения системы к идеальной, для которой эксергетический к. п. д. равен единице.

Перед составлением балансов необходимо выделить систему, подле­жащую исследованию, для чего мысленно отделяют ее от других объектов контрольной поверхностью, а эксергии всех проходящих через нее потоков вещества и энергии включаются в эксергетический баланс.

Для ш кг вещества в единицу времени или за определенный период эксергетический баланс ЭХГС имеет следующий вид:

I Ей = Ї E2J + '£" Ц + X А, (1-243)

І=І Г = і і = і

Или

ZD, = I Еи - (уІЕгл + £ іЛ (1.244)

І = І ;=і І=І І=І /

I-N I~N

Где £ EJti и £ E2,I — сумма входящих в ЭХТС эксергий и выходящих і = 1 і = 1

Из нее соответственно, сюда входят все виды эксергии, рассмотренные

Рис. 1.50. Eh-Диаграмма Рис. 1.51. К определению Эксергетического баланса машины

І я и I = п

Выше; Е Li — сумма работ, совершаемых в ЭХТС; Е — сумма эк - «=і /=і

Сергетических потерь ЭХТС.

В открытых системах эксергия Ev — 0. В закрытых системах, где отсутствует обмен веществом через границы системы, равны нулю эксергии потока вещества и нулевая эксергия. Однако в химических реакторах периодического действия нулевая эксергия при химических превращениях является основной.

На основании эксергетического баланса определяются относительные или абсолютные характеристики ЭХТС и ее отдельных частей.

Рассмотрим эксергетические балансы отдельных элементов ЭХТС. Любая ЭХТС в общем случае состоит из машин и всевозможных аппаратов.

Эксергетический баланс любой машины составляется на основании схемы, изображенной на рис. 1.51: для т кг вещества

Xf £1>г= £ E2.T + L+D; (1.245)

/= 1 i=l

При D — 0

L='f Еи - '£Е2>і, (1.246)

1=1 і = 1

Т. е. при обратимом процессе в машине работа, совершаемая ею или затраченная на ее действие, равна изменению эксергии на входе и выходе из нее.

Для 1 кг вещества эксергетический баланс машины напишется аналогичным образом

EVi=' 'Јe2ti + l + d. (1.247)

І- 1 i=l

Для любого аппарата ЭХТС эксергетический баланс запишется в виде для т кг вещества

ЈEU= Ё" E2J + D; (1.248)

І=1 1=1

Для 1 кг

І = п І = п

Е «1.1 = Е + d. (1.249)

Ї=1 і = 1

І = п і = и

При D = 0 Е EUi — Е Е2,і, Т. е. при обратимом процессе в аппарате i=i I=I

Эксергия вещества, находящегося в нем, не изменяется. 80

Очевидно, совершенство ЭХТС и ее элементов тем выше, чем меньше потери эксергии, и поэтому степень совершенства ЭХТС и ее элементов обычно характеризуют так называемым эксергети - ческим к. п. д., который определяется из эксергетического баланса, а именно: для ЭХТС

І-п і = и і — п І = И

І е2,І + Z и Z EU - Z DI I=l Ј=1 (=1 i=l

Л« = -------- Г=ПІ-------- =---------- ^-------------- ; (1.250)

Z Z Eu

І = І і = і

Для машин

2 Е2,І + L Z El,I - D

Л« = ^------------ = ^------------- Ї d-251)

Z Eи Z Eu

X = 1 1=1

Для аппаратов

ЈE2J X Eu-D

^------------------------------- • (1.252)

Z Eu £ Eu

Очевидно, для ЭХТС и ее элементов при отсутствии потерь

І = 11

На необратимость (потерь эксергии), т. е. при £ D,- = 0, эксергетиче-

І = 1

Ский к. п. д. будет равен 1.