ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ ДЛЯ РАБОЧЕГО ТЕЛА, НАХОДЯЩЕГОСЯ В ОТНОСИТЕЛЬНОМ ПОКОЕ (ЗАКРЫТАЯ СИСТЕМА)
 19 марта, 2013
19 марта, 2013  admin
admin В данном случае, поскольку центр массы рабочего тела не перемещается, внешняя кинетическая энергия рабочего тела будет величиной постоянной и изменение ее будет равно нулю. Тогда первый закон термодинамики можно записать в следующем виде:
Q = AU + L, (1.30)
|
(1.25) (1.26) (1.27) (1.28) |
Где L— работа расширения-сжатия для т кг рабочего тела, Дж.
Для 1 кг рабочего тела первый закон термодинамики выглядит так:
Q = Аи + I. (1.31)
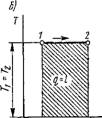
Найдем математическое выражение работы расширения-сжатия и дадим ей графическое толкование. Пусть в результате протекания термодинамического процесса рабочее тело массой т кг увеличится в объеме на DV (рис. 1.1). В случае равномерного распределения по поверхности рабочего тела давления среды элементарная работа против этого давления в результате увеличения объема тела от V до V + D К будет равна сумме элементарных работ перемещения элементарных площадок d/ первоначальной поверхности рабочего тела на элементарном пути DS, т. е.
Со
SL = X>d/dS = fpd/dS, і
Где р Df — элементарная сила.
На элементарном пути dS давление р можно считать постоянным и тогда элементарная работа будет:
5L = р Jd/dS = pdV, (1.32)
Так как J Df DS — есть сумма бесконечно большого числа бесконечно малых объемов, т. е. приращение объема рабочего тела DV.
Так как всегда р > 0, то работа будет положительной, если DV > 0, т. е. когда рабочее тело расширяется. Следовательно, положительная работа есть работа расширения. Если DV < 0, т. е. рабочее тело сжимается, то работа будет отрицательной; следовательно, Отрицательная работа есть работа сжатия, совершаемая внешним источником энергии над газом.
В соответствии с уравнением (1.32) элементарная работа 1 кг рабочего тела
8/ = р Dv, (1.33)
Где 8 — знак неполного дифференциала.
Когда рабочее тело изменяет свое состояние от значений параметров Pt, Ті и VІ до рг, Т2 и V2, оно совершает работу, равную
L = ^pdv. (1.34)
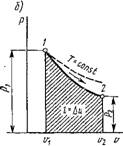
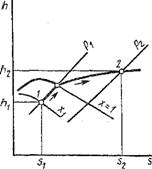
В координатах р, v (рис. 1.2) изобразим равновесный термодинамический процесс 1-2. При изменении объема 1 кг рабочего тела на бесконечно малую величину Dv можно считать давление постоянным. Тогда площадь заштрихованной элементарной площадки будет равна рDv, а вся площадь а2Ь - сумме этих элементарных площадок, т. е.
Пл. A2B — J"1 р di' = /.
Следовательно, работа расширения-сжатия численно равна площади
в координатах р, и, ограниченной кривой процесса, начальной и конечной ординатами и осью абсцисс.
|
Рис. 1.2. Графическое изображение работы расширения- сжатия в координатах р, V |
|
Рис. 1.1. К определению работы расширения-сжатия |
Из рис. 1.2 и формулы (1.34) следует, что в отличие от внутренней энергии работа является функцией процесса, а не состояния.
|
(1.35) (1.36) |
|
(1.37) |
Зная математическое выражение работы расширения-сжатия, формулы (1.30) и (1.31), представляющие собой математическое выражение первого закона термодинамики, можно представить в виде
Q = AU + fv2lPdU; q — Аи 4- J^J р dv
И в дифференциальной форме
8 Q — du + р dv.
Из этих формул видно, что теплота, равная изменению внутренней энергии и работы, будет зависеть от характера протекания термодинамического процесса. Отсюда следует, что если дифференциал внутренней энергии есть полный дифференциал, то дифференциал теплоты, так же как и дифференциал работы, не является полным дифференциалом.
|
|
|
Dp. (1.40) |
|
(1.38) |
|
(1.39) |
Подставляя в уравнение (1.37) значения du из уравнений (1.25) — (1.27), получим
Если в уравнение (1.37) подставить р Dv — d (Pv) — V Dp, то получим 5Q = Du + D(Pv) — Vdp = D(U + Pv) — и dp. (1.41)
Так как данным значениям р и V соответствует единственное значение и, то (и + Pv) есть функция термодинамического состояния рабочего тела, т. е. его параметр состояния; этот параметр называют Энтальпией и обозначают H. Ее единица — Дж; единица удельной энтальпии — Дж/кг. Следовательно, с учетом уравнения (1.41) первый закон термодинамики может быть записан так:
6Q = dh — v dp. (1.42)
В изобарном процессе (р = const) V dp = 0 и, следовательно,
5 qp = dh, (1.43)
Т. е. количество энергии, сообщенное рабочему телу в форме теплоты в изобарном процессе, равно изменению его энтальпии.
Теплоемкость газов. Отношение количества теплоты, сообщаемой системе (телу) в каком-либо процессе, к соответствующему изменению температуры называется теплоемкостью. Теплоемкость тела, соответствующая бесконечно малому изменению температуры, называется истинной теплоемкостью, т. е.
С = SQ/DT. (1.44)
Теплоемкость тела, соответствующая изменению температуры на конечную величину, называется средней теплоемкостью тела, т. е.
Ст = Шг - fx). (1.45)
Теплоемкость единицы массы называется массовой удельной теплоемкостью или просто массовой теплоемкостью и обозначается буквой с, ДжДкг • К).
Теплоемкость единицы объема при нормальных условиях называется объемной удельной теплоемкостью или просто объемной теплоемкостью. Она обозначается буквой с', Дж/(м3 ■ К).
Теплоемкость 1 кмоля тела называется мольной теплоемкостью Цс, ДжДкмоль • К). Из этих определений вытекает следующая связь между массовой, объемной и мольной теплоємкостями:
С = с' V = цсДі. (1-46)
Так как теплота зависит от процесса, то теплоемкость есть функция процесса, и поэтому всегда говорят о теплоемкости того или иного процесса. Это обстоятельство учитывается при написании той или иной теплоемкости, например: массовая теплоемкость при постоянном давлении обозначается ср, мольная теплоемкость при постоянном объеме — объемная средняя теплоемкость при постоянном объеме — C'Vm и т. д.
С учетом уравнения (1.39) массовая теплоемкость термодинамического процесса любого рабочего тела
|
Я I +Р Dv IT |
Ди
_ Bq _ / ди c~~df~[~df] +
Из этой формулы можно получить выражение массовой теплоемкости в любом термодинамическом процессе. Так, массовая теплоемкость при постоянном объеме, или изохориая теплоемкость, очевидно, будет равна
- __ / D" С°~ Dт~дт);
(1.48)
Отсюда следует, что если известно с„ для реального рабочего тела, то можно найти изменение его внутренней энергии в изохорном процессе:
Duv = cvdT. (1.49)
Согласно квантовой теории теплоемкости изохорная теплоемкость идеального газа является функцией только температуры и поэтому для него в любом термодинамическом процессе изменение внутренней энергии может быть рассчитано по формуле
Du = cv dT, (1.50)
Или
Au = ^c0dT. (1.51)
С учетом (148) теплоемкость термодинамического процесса для любого рабочего тела может быть выражена уравнением
|
D Г' Dv IT |
|
Ди |
|
(1.53) |
|
- Д (RT |
|
Dv ~дТ |
|
= 0; |
|
(1.54) |
Dy
(1.52)
C = cv-1-
Отсюда изобарная теплоемкость
Cp = Cv +
Для идеального газа
МЛ = FcvdT dv )т dv )т
И, следовательно, для него
(1.55)
Ср = Cv + R.
Эта формула, называемая законом Майера, является одной из важнейших в теории теплоемкости. Из формулы (1.54) видно, что
|
R |
Р Dv
(1.56)
ДТ
Т. е. газовая постоянная есть удельная работа газа в изобарном процессе при изменении температуры на один градус.
Умножая формулу (1.55) на ц, получим, что мольная теплоемкость идеального газа
Цср = цс„ + 8314. (1.57)
Поделив уравнение (1.57) на объем 1 кмоля, при нормальных условиях, т. е. на 22,4 м3/кмоль, получим, что объемная изобарная теплоемкость идеального газа
С'р — C'V 4- 371,2. (1.58)
Так как изменение энтальпии численно равно теплоте изобарного процесса, то массовая изобарная* теплоемкость может быть рассчитана по формуле
Отсюда следует, что изменение энтальпии любого рабочего тела в изобарном процессе может быть рассчитано через изобарную теплоемкость:
Dhp = с pdT. (1.60)
Согласно квантовой теории теплоемкости изобарная теплоемкость идеального газа зависит только от температуры, и поэтому в любом термодинамическом процессе идеального газа изменение энтальпии может быть найдено из формулы
Dh = cpdT. (1.61)
Как указывалось выше, молекулярно-кинетическая теория для идеального газа дает линейную зависимость внутренней энергии от температуры [см. формулу (1.24)]. В этом случае теплоемкость идеального газа не зависит от температуры, так как
Ь DT dT v
Для одноатомных газов І = 3, и поэтому для них цс„ = 4155 • 3 — = 12465 и іср »цс„ + 8314 = 20779 ДжДкмоль • К). Соответственно для двухатомных газов (/ = 5) xcv = 4155 • 5 = 20 775 и цср = 20 775 4- 8314 = = 29 089 ДжДкмоль • К). Наконец, для трехатомных газов и более (г = 7) цс„ = 4155 • 7 = 29085 и цср = 29085 + 8314 = 3,74-104 ДжДкмоль • К). Найденные опытным путем мольные теплоемкости для реальных одно - и двухатомных газов при температурах 15...20°С удовлетворительно согласуются с вычисленными по формуле (1.62) величинами. Однако для трехатомных газов получаются большие расхождения вычисленных значений мольных теплоемкостей с экспериментально найденными. Опытами установлено, что для двух- и многоатомных газов теплоемкость зависит от основных параметров состояния и в первую очередь от температуры. Для реальных газов, практически подчиняющихся уравнению состояния Менделеева — Клапейрона, теплоемкость можно принять не зависящей от давления. Однако для сжатых газов и паров влияние давления на теплоемкость весьма значительно.
Как общее явление, теплоемкость газов возрастает с повышением температуры. Согласно новейшим опытным исследованиям зависимость теплоемкости от температуры весьма сложная и для каждого газа имеет свой характер, и поэтому при всех термодинамических расчетах следует пользоваться таблицами, составленными по опытным материалам.
Отношение изобарной теплоемкости к изохорной называют коэффициентом Пуассона и обозначают буквой к:
К = cp/cv = c'p/c'v = xcp/[icv. (1.63)
Согласно молекулярно-кинетической теории газов, можно написать,
Что
Iicv + 8314 4155/ + 8314 < 2
К =----------------- =--------- ——------ = 1 + —. (1.64)
Lie, 4155/ І 1
Для одноатомных газов / = 3 и, следовательно, к = 1,667, для двухатомных газов І = 5 и /с = 1,4 и, наконец, для трехатомных газов и более / = 7 и к = 1,29. Опытные данные по определению коэффициента Пуассона для реальных газов удовлетворительно согласуются с расчетными по формуле (1.64) только при невысоких температурах. Так как для реальных газов теплоемкость возрастает с повышением температуры, то, очевидно, величина к должна уменьшаться:
H __ [LCP _ VLCp + 8314 _ 1 8314 _ 8314
Fc — — -------------------- — 1 Н-------- — 1 + ------ ;—----------- .
|іс„ цс„ |іс„ а + bt + ...
Так, для двухатомных газов экспериментально установлено, что К = 1,4 - 0,00005г.
Зная теплоемкость газов, нетрудно вычислить теплоту данного
Термодинамического процесса. В самом деле, из формул (1.44) и (1.45) следует, что
&Q = cdT, q = с dt, (1.65)
Или
Q = cm{t2 - її). (166)
Понятно, что в технических расчетах формула (1.66) предпочтительнее формулы (1.65). При пользовании формулой (1.66) необходимо уметь вычислять среднюю теплоемкость в заданном интервале температур от до T2. Для этой цели выразим среднюю теплоемкость ст в интервале температур от fx до T2 через средние теплоемкости от 0 до H и от 0 до T2, которые обычно приводятся в справочной литературе. Зависимость теплоемкости от температуры дана на рис. 1.3, из которого видно, что площадь заштрихованной элементарной площадки равна Cdt — Bq, и, следовательно, площадь а!2Ь, Равная сумме этих элементарных площадок, т. е. jj^Cdt, есть теплота процесса на участке 1-2. Построив прямоугольник а34Ь, равновеликий пл. а12Ь, получим в качестве высоты его среднюю теплоемкость с,„, построенную на участке 1-2. Таким образом, можно написать, что
Пл. Al2B — с dt = Q — cm(i2 — 11). (1.67)
Аналогично можно написать, что
Пл. Oola = Jfl cdt =
= cMi {h ~ 0)°= cmlti (1.68)
Пл. Oo2b = $hcdt = = C„2 ih - 0) = cm2t2. (1.69) Из рис. 1.3 видно, что пл. al2b =
= пл. Oo2b — пл. Oola. Подставляя в уравнение (1.70) вместо площадей их выражения через средние теплоемкости по уравнениям (1.67), (1.68) и (1.69), получим
|
(1.71) |
- *i) = cm2t2 - cmitu
Откуда
Ст2Ї2 ~ Cml^L T2 - ti
Если газовая смесь находится в равновесном состоянии, то, очевидно, количество теплоты смеси равно сумме теплот компонентов,
Л
Т. е. бсм = Y, 6ь и поэтому, например, массовую теплоемкость смеси 1
|
(1.72) |
Можно найти следующим образом:
FnCMcCMAtCM = ]Г mjCj AtCK
Откуда
И и
|
Рис. 1.3. Зависимость теплоемкости от температуры |
= ) Ci = ) Qid.
|
(1.74) |
Li™™ Zj
Рассуждая аналогичным образом, получим формулы для вычисления объемной и мольной теплоемкостей смеси:
(1.73)
ЦСсм = X ri1Ci-
Энтропия. В математике доказывается, что если дифференциал какой-либо функции нескольких переменных не есть полный дифференциал, то всегда можно найти такую функцию, при умножении на которую этот дифференциал превращается в полный. Такая функция называется интегрирующим множителем.
Интегрирующим множителем дифференциального уравнения теплоты является величина, обратная абсолютной температуре, т. е. 1/Т. Напишем, например, уравнение (1.39) с учетом уравнения (1.48):
|
Dv |
|
(1.75) |
Ди
■ +р
Ь Q = cvdT +
Dv
И умножим его на интегрирующий множитель 1/Т, тогда получим полный дифференциал некоторой функции термодинамических параметров состояния
|
Bq_ Т |
|
Dv T |
|
D T С» - jr + |
|
(1.76) |
|
Ds |
|
+ P |
Для того чтобы показать, что уравнение (1.76) действительно является полным дифференциалом, надо иметь конкретную зависимость между термодинамическими параметрами состояния. Так, для идеального газа duT=f«dT и р = RT/v, тогда, подставляя эти значения в уравнение (І.76), получим
СIT _ Dv
|
8Q |
|
(1.77) |
|
Ds = |
Су —=r + R — T v
Нетрудно видеть, что уравнение (1.77) представляет собой полный дифференциал. В самом деле, интегрируя это уравнение, получим
F
S2 ~ Si
Из этого уравнения видно, что изменение параметра s не зависит от процесса, а определяется исключительно начальными и конечными значениями Т и v. Величина s, являющаяся функцией параметров состояния, сама может быть рассмотрена как функция состояния. Впервые эту функцию нашел Р. Клаузиус при анализе второго закона термодинамики и назвал ее энтропией. Он показал (см. с. 65), что дифференциал энтропии ds = бq/T является полным дифференциалом для реального рабочего тела, находящегося в любом агрегатном состоянии. Как следует из уравнения (1.76), единица удельной энтропии — ДжДкг • К).
Поскольку три основных параметра рабочего тела связаны между собой уравнением состояния, энтропию его можно выражать не только как s — f(T, v), но и как s = ср (Т, р) и s = v|/ (р, v).
|
1 , D, у2 Cv In —;—b R 111-- 71 |
|
(1.78) |
Для реального рабочего тела уравнение (1.40) путем несложных преобразований [с учетом формул (1.40), (1.53) и (1.59)] можно привести к виду
|
Bq |
|
C'pdT |
(1.79)
И, следовательно,
|
Л |
|
Ds |
(1.80) 21
Dp
Ds = с,
S2 - Sl = ср In (Т2/Ті) - Л In (р2/ра). (1.83)
Следовательно, если для данного рабочего тела известна его энтропия и один из основных параметров состояния, то тем самым термодинамическое состояние этого тела вполне определено.
Отсюда следует, что линия в любых координатах Т, S; р, Т или Т, V будет изображать равновесный термодинамический процесс. Наряду с координатами р, V в термодинамике находят широкое применение координаты Т, S, поскольку в них можно графически определить теплоту процесса и истинную массовую теплоемкость. Докажем эти два весьма ценные - свойства Т, s-диа - граммы.
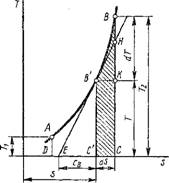
На 75-диаграмме, изображенной на рис. 1.4, кривая АВ представляет термодинамический процесс. Если пренебречь бесконечно малой величиной высшего порядка, то площадь заштрихованной элементарной площадки будет равна Tds, а так как ds = Bq/T, то, следовательно, эта площадь равна Tds = 8Q. Площадь ABCD равна сумме элементарных площадок, т. е. пл. ABCD = j Т ds = j 8Q = Q - теплоте термодинамического процесса АВ, что и требовалось доказать.
Так как всегда Т > 0, то положительному приращению^ энтропии соответствует положительное приращение энергии в форме теплоты. Другими словами, увеличение энтропии связано с подводом теплоты в данном термодинамическом процессе и, наоборот, уменьшение энтропии — с отводом теплоты. Следовательно, процесс, изображенный на рис. 1.4, протекает с подводом теплоты к рабочему телу.
Если провести касательную к линии процесса АВ в точке Вто подкасательная ЕС дает значение массовой теплоемкости в данном состоянии рабочего тела по величине и знаку. В самом деле, из подобия треугольников ЕВ'С и В'НК следует, что ЕС/СВ' = KB'/КН. Так как С'В' = Т; В'К = DS и КН = dТ, (с точностью до второго порядка малости), то
|
Св, |
ЕС
В'К
СВ'
~Df
КН d Т
|
Для идеального газа ~ <r J)p~j |
|
|
|
Или |
|
Рис. 1.4. Графическое изображение теплоты и теплоемкости процесса в координатах Т, S |
|
Dv ІТ |
|
(1.81) |
|
Подставляя выражение (1.81) в уравнение (1.80), получим |
|
6Т Т |
|
R |
|
(1.82) |
|
Ds |
Что и требовалось доказать. Подкасательная положительна, т. е. с > 0, Если она лежит влево от вертикали, проведенной через данную точку кривой, и, наоборот, отрицательна, если лежит вправо.
Термодшмяшзе процессы, протекающие в идеальном газе. Термодинамический процесс, протекающий в идеальном газе при постоянной теплоемкости, называется политропным. Политропный процесс характеризуется заданны;.! коэффициентом а распределения теплоты между изменением внутренней энергии Дм и работой /. Для каждого поли- тропного процесса а — Au/Q — const. Выведем уравнение политропы.
Для идеального газа в соответствии с уравнениями (1.37), (1.42), (1.50) и (1.61) можно написать:
БQ = с„ с! Т ~ с, D Т + pdv и 5Q = с„ с1Г = с,, сГГ- v dp,
Или
(с„ - cv)dT=pdv, (1.84)
(с'п - с,,) dT — - vdp. (1.85)
Поделив уравнение (1.85) на (1.84), получим
(с„ - с,,)/(сп - С) = - V Dp/ip dv).
Так как из определения политропного процесса теплоемкости являются величинами постоянными, то, обозначив
(с„ - с,,)/(с„ - с„) = п, (1.86)
Получим
Vdp Du dp
П ---------- f - или п — + - І - = 0. (1.87)
Pdv v р
В результате интегрирования этого уравнения имеем п in v + In Р — = const, или In (Pv") — const, или
Pvn = const. (1.88)
Уравнение (1.88) называется уравнейием политропы, а показатель этого уравнения п — показателем политропы.
Исследование политропного процесса, как и других термодинамических процессов, будем проводить в такой последовательности.
/ I. Найдем связь между основными параметрами состояния: так как РIf" = Pzv'L то
Рї/Р2 = (vz/viT и оаМ = (Pl/р2)1/п. (1.89)
Совмещая уравнения (1.89) с уравнением состояния идеального газа (1.3), получим
Ті/Тг = (v2/vi)"- Или TJT2 = {ру/ргГ'Х),п- 0-90)
2. Работа газа: l — f^pdv. Подставляя в это выражение р-р11?Г/г?",
Получим
(1.91)
V Jlj
Заменяя в этом уравнении отношение объемов на отношение температур из уравнения (1.90), получим
I = —~(Тг - Тг) = —Ц-(Рі»І - p2v2). (1.92)
N — 1 n — I
Подставляя в уравнение (1.91) вместо отношения объемов отношение давлений из уравнения (1.89), получим
/= ^[1-(P2/P1)(',-1)/'']. (1.93)
П — і
3. Теплоемкость процесса найдем из формулы (1.86): сп~с,,= — яе„ — пс,„ или сп — кс = пс„ — пс„, откуда
П — к
Сп = --------- г - (1.94)
П — 1
4. Теплота процесса
Q = | cudT= IС, ILJLDf = c0 ^—^(h - tx). (1 95)
1 1 n — 1 n — l
'і
5. Изменения внутренней энергии, энтальпии и энтропии не зависят от процесса и поэтому д ія любого процесса, протекающего в идеальном газе, их можно вычислить по формулам (1.50), (1.61), (1.78) и (1.83). Наряду с этим при исследовании политропных процессов для: вычисления энтропии нашла применение следующая формула:
БQ Г1 N-K DT п - к Т2
|
As |
-г - L п— ~т ^ е> —1пТі • (1%)
6. Доля теплоты, идущей на изменение внутренней энергии,
А" * / п ~ ^ а п—І
А =-- = с„ Д// с„------ At =--------- -. . 1.97
Q п — I J п — к
7. Доля теплоты, идущей на работу,
: / , 1 - к
— = 1 - а = ~----------- т (1.98)
Q к — п S '
8. Показатель политропы можно определить путем логарифмирования формулы (1.89):
N=>g(pxlpi)/g{vi/vx). (1.99)
Основные термодинамические процессы в идеальном газе — частные случаи политропных процессов. При п = 0 уравнение политропы (1.88) принимает вид р = const, т. е. в этом случае будем иметь изобарный процесс. Для этого процесса уравнение состояния принимает вид
В/Г = R/P = const. (1.100)
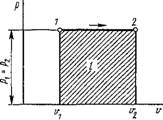
На рис. 1.5 изобарный процесс представлен в координатах р, V. Площадь заштрихованного прямоугольника есть работа процесса, равная
/„ = р Dv = р (v2 - Vi) = R(T2 — 71). (1.101)
Теплота процесса
|
Її) = Ah. |
|
(1.102) |
Qp = $'*Cpdt = Cp(T2 Изменение энтропии в процессе
Г 5q Г» cpdT
|
In |
|
(1.103) |
|
V |
= J J ^ t~ = cp
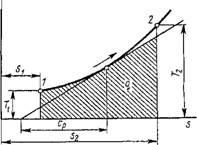
Откуда следует, что в координатах Т, S процесс изображается логарифмической кривой 1-2 (рис. 1.6). В соответствии с вышеизложенным, на рис. 1.6 графически изображены теплота и теплоемкость процесса: при направлении процесса от І к 2 теплота подводится к газу и теплоемкость имеет положительное значение.
Как следует из формулы (1.97), а= 1/к. Это значит, что, например, для двухатомных газов
А = 1//с = 1/1,4 = 0,714,
Т. е. из всей подведенной в процессе теплоты со 71 % расходуется на изменение внутренней энергии и только со 29 % — на работу.
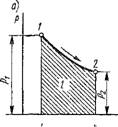
Напишем уравнение политропы (1.88) в виде P1/NV = const. Тогда, подставляя п= ±оо, получим V — const — изохорный процесс, который в координатах р, V изображается прямой, параллельной оси ординат (рис. 1.7, а). Отсюда следует, что работа в изохорном процессе равна нулю. Для этого процесса уравнение состояния Менделеева — Клапейрона примет вид
Р/Т = R/V - const. Теплота изохориого процесса
Qv = J't*c„ dT = Cv (t2 - Ti) = Au. Изменение энтропии в процессе
|
(1.104) (1.105) (1.106) |
|
Asv |
|
Т |
Г' cvdT
Т
С„ In
Гу
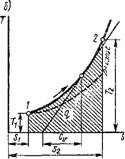
Откуда следует, что в координатах Т, S процесс изображается логарифмической кривой 1-2 (рис. 1.7, б). В соответствии с вышеизложен-
|
Рис. 1.5. Изображение изобарного процесса в координатах р, V |
Т
|
Рис. 1.6. Изображение изобарного процесса в координатах Т, S |
|
1/, ITj tr |
|
Рис. 1.7. Изображение изохор - ного процесса в координатах р, и и Т, S |
|
Рис. 1.8. Изображение изотермического процесса в координатах р, V и Т, S |
|
3-J $2 $ |
Ным, на рис. 1.7,6 графически изображены теплота, подведенная к газу, и положительная теплоемкость процесса.
При сравнении формул (1.103) и (1.106) можно видеть, что если Ср > ct„ то в одном и том же интервале температур Ті и Т2 изменение энтропии в изобарном процессе будет больше, чем в изохорном. Отсюда следует (см. рис. 1.7,6), что кривая изохорного процесса 1-2 будет круче кривой изобарного процесса 1-2' ив одном и том же интервале температур теплота изобарного процесса будет больше теплоты изохорного процесса (на величину работы).
Для изохорного процесса а = 1, т. е. вся теплота идет на изменение внутренней энергии газа.
При п — 1 уравнение политропы принимает вид Pv = const или Т = const — изотермический процесс. Так как связь между параметрами этого процесса будет рIt»i = P2V2, то кривой процесса в координатах Р, V будет равнобокая гипербола (рис. 1.8, а). Площадь под кривой 1-2 — Это работа процесса, равная
PlVl = PiVl In -2- = RTn (1.107)
Рг
Vi
|
H |
|
P dv — |
Так как в этом процессе Ди = Cv(T2 — fi) = 0, то
QT- Ди + / = /,
Т. е. в изотермическом процессе подведенная к идеальному газу теплота расходуется только на совершение ею работы расширения, и, следовательно, в этом процессе а = 0.
Изменение энтропии в изотермическом процессе
Д*Г= f-^Uifs = (1.109)
Отсюда следует, что в координатах Т, S (рис. 1.8,6) теплота изотермического процесса равна площади прямоугольника с основанием As и высотой Т.
При п = к уравнение политропы принимает вид Pvk = const. Это уравнение является уравнением изоэнтропийного, или обратимого, адиабатного процесса, основным свойством которого для любого рабочего тела является отсутствие теплообмена между последним и окружающей средой, поскольку 6qs — сп dt = 0, так как
П — к к — к
Си = Cv -------- = с„ ---------- = 0.
П — 1 п — 1
Как будет показано ниже, уравнение адиабатного процесса Pvk = const
Справедливо только при протекании его в идеальном газе. Уравнение же 5Qs = 0 справедливо для протекания адиабатного процесса в любом рабочем теле, и поэтому оно является наиболее общим уравнением этого процесса.
Связь между параметрами состояния, а также работа адиабатного процесса в идеальном газе находятся по соответствующим формулам для политропного процесса с заменой показателя политропы п на показатель адиабаты к. Отсутствие теплообмена при протекании адиабатного процесса указывает на то, что в соответствии с первым законом термодинамики работа в этом процессе совершается за счет внутренней энергии: Qs — Аи + I — 0, т. е.
H = ux-u2. (1.110)
Другими словами, адиабатное расширение связано с понижением температуры рабочего тела и, наоборот, сжатие — с повышением ее. Так как в адиабатном процессе Bqs = 0, то для него ds = Bq/T — 0, или
5 = COnSt, (1.111)
Т. е. обратимый адиабатный процесс является процессом изоэнтропий - ным. Следовательно, в координатах Т, S (рис. 1.9, а) адиабатный процесс изобразится в виде прямой, параллельной оси ординат. В координатах р, V адиабата изображается неравнобокой гиперболой Pvk = — const, а так как к > 1, то адиабата 1-2 будет круче изотермы 1-2' (рис. 1.9, б). Отсюда следует, что при одинаковой степени расширения г2/і'і работа адиабатного расширения будет меньше работы изотермического расширения и, наоборот, при одинаковой степени сжатия V2Jx> Работа адиабатного сжатия на участке 2-1 будет больше работы изотермического сжатия.
Классификация политропных процессов позволяет качественно оценить любой термодинамический процесс в идеальном
|
N--H
|
|
/7=+оо N = k |
Рис. 1.9. Изображение адиа - Рис. 1.10. К классификации
Батиого процесса в коорди - политропных процессов
Натах р, v и Т, s
|
|
|
V |
|
Sfh |
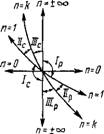
Газе, не прибегая к аналитическому решению. На рис. 1.10, а, б изображены основные термодинамические процессы в идеальном газе, а бесконечно большое количество остальных политропных процессов будут расположены между ними. На Pv- и Ts-графиках (рис. 1.10, а, б) изохора п = +00 делит все политропные процессы на протекающие при расширении газа (справа от изохоры) и протекающие при сжатии газа (слева от изохоры). Сначала установим классификацию для случая расширения газа. В изобарном процессе расширение газа имеет место только при подводе теплоты к рабочему телу, при этом внутренняя энергия увеличивается, а следовательно, температура газа возрастает (рис. 1.10, б). В изотермическом процессе расширение газа также связано с подводом к газу теплоты, причем внутренняя энергия его не изменяется. В адиабатном процессе расширение газа происходит за счет внутренней энергии, а следовательно, температура газа уменьшается (рис. 1.10,6). Очевидно, изохора с показателем политропы п=+ со Есть изохора охлаждения, т. е. в этом процессе теплота отводится и внутренняя энергия уменьшается. Тогда изохора п = — оо есть изохора нагревания; в этом процессе теплота подводится и идет на увеличение внутренней энергии газа. Вышесказанное позволяет разбить все политропные процессы с и от - со до +оо при расширении газа на три группы, а именно:
I группа: — соси. <1. В этой группе, как видно из рис. 1.10,6, dT> 0, а следовательно, du = cvdT> 0 и dH = cpdT> 0; здесь ds > 0, а следовательно, bq > 0. Так как cn = 5g/dT>0, то теплоемкость в этой группе процессов положительная. Подведенная к газу теплота расходуется на увеличение внутренней энергии и на совершение им работы расширения;
II группа: 1 < п < к. Как видно из рис. 1.10,6, для этой группы dT< 0, а следовательно, du < 0 и dh < 0; ds > 0 и, следовательно, bq>0 Теплоемкость в процессах отрицательная, так как сп = bq/dT < 0. Термодинамические процессы второй группы характерны тем, что работа расширения совершается как за счет подведенной к газу теплоты, так и за счет внутренней энергии;
III группа: к<п<+со. Здесь (рис. 1.10,6) при расширении газа все параметры состояния уменьшаются (dT < 0, du < 0, dh <0, ds < 0), 6Q < 0, но теплоемкость cn = bq/dT> 0, т. е. положительная. В процессах этой группы расширение газа происходит с уменьшением его внутренней энергии и отдачей теплоты в окружающую среду.
Как видно из рис. 1.10, а, б, в случае сжатия газа все политропные процессы делятся на те же три группы, но с противоположными знаками у параметров состояния и теплоты. Теплоемкость процесса в каждой группе, естественно, будет иметь те же знаки, как и при расширении газа.
|
(1.112) (1.113) |
|
|
|
|
|
|
Термодинамические процессы, протекающие в реальном газе. В инженерной практике, за исключением процессов, протекающих в компрессорах, мы встречаемся с четырьмя основными термодинамическими процессами, а именно: изобарным, изохорным, изотермическим и адиабатным. Обычно при р <§; /;кр и Т» Ткр реальные газы можно рассматривать как идеальные и для них уравнением состояния является уравнение Менделеева — Клапейрона (1.4). В этом случае связь между основными термодинамическими параметрами и работа расширения-сжатия рассчитываются по формулам, приведенным в предыдущем параграфе. Изменение внутренней энергии, энтальпии и энтропии в термодинамическом процессе рассчитывается по нижеследующим формулам с учетом температурной зависимости теплоемкости:
А и - J J с0 D Т = cvm (Т2 - ТО; А/? = cpdT= cpm(T2 — Tj);
- для изобарного процесса;
(1.115)
- для изохориого процесса;
— для изотермического процесса, поскольку при условии зависимости Cv только от температуры в этом процессе А и — 0.
Теплота в изохорном процессе равна А и, в изобарном Ah и в изотермическом I.
При высоких давлениях или температурах, близких к критическим, газы не подчиняются уравнению Менделеева — Клапейрона; внутренняя энергия и энтальпия, а следовательно, и теплоемкость зависят не только: от температуры, но и от давления. Для реальных газов связь между основными параметрами состояния устанавливается уравнением Ван дер Ваальса, если можно пренебречь энергией ассоциации молекул. В тех случаях, когда энергией ассоциации молекул пренебречь нельзя, связь между р, v и Т можно найти из уравнения (1.19). Однако это уравнение пока не нашло практического применения из-за сложности вычисления вириальных коэффициентов. Поэтому связь между Р, V и Г находят либо из соответствующих таблиц для данного газа, приведенных в теплотехнических справочниках, либо из эмпирических уравнений.
Для составления эмпирического уравнения состояния какого-либо газа используют опытные данные, полученные по зависимости между P, V и Г, или по зависимости теплоемкости этого газа от основных параметров состояния, или по температурному эффекту дросселирования.
Рассмотрим, например, составление эмпирического уравнения состояния для реального газа на основании опытных данных по его теплоемкости. Используя свойство полного дифференциала, из уравнения (1.80) можно написать, что
Dp Tjr дт дТ Откуда
На основании опытных данных составляется эмпирическое уравнение ср — ф (Г, р). Берется частная производная (сср/др)т и подставляется в уравнение (1.11 7):
Щ - -
Интегрируя дважды это уравнение, получают эмпирическое уравнение состояния для данного реального газа.
Энтальпию реального газа для данного р и Г либо находят непосредственно из соответствующих термодинамических таблиц, либо рассчитывают по формуле
H = cpmt, (1.119)
Где гг„. — средняя изобарная теплоемкость от 0 °С до T — берется из соответствующих таблиц теплоемкостей данного газа при данных р и T.
Внутреннюю энергию реального газа для данного его состояния, характеризующегося параметрами р, V и Г, вычисляют по очевидной
Формуле
H — pv.
Энтропию реального газа для данных р и Г находят непосредственно из соответствующих термодинамических таблиц.
Для реальных газов, не подчиняющихся уравнению Менделеева — Клапейрона, в изотермическом процессе теплота процесса рассчитывается через энтропию, т. е. qT— T(s2 — .Vi), а работа —
Через первый закон термодинамики LT= QT— А и. Для адиабатного процесса, поскольку Qs = 0, работа процесса также найдется через первый закон термодинамики, а именно: Ls = — Аи = (Их — H2) - (PiVi - P2V2)- Теплоты изобарного и изохорного процессов соответственно равны Ah И Aw. Работа в изобарном процессе, очевидно, равна
1Р = р Du = р (У2 - fi).
Термодинамические процессы, протекающие в парах. С качественной точки зрения поведение паров всех веществ одинаково и поэтому процесс превращения жидкости в пар рассмотрим на примере самого распространенного на Земле и самого изученного вещества — воды.
|
Рг-диаірамма Водяного Пара |
|
(1.120) |
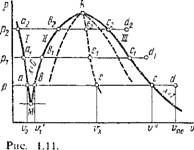
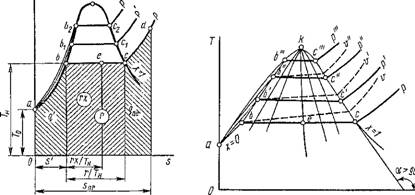
Пусть мы имеем 1 кг воды в момент получения ее из твердого состояния, т. е. при температуре плавления. Все параметры жидкости при температуре плавления будем обозначать индексом «0». Изобразим это состояние жидкости, в частности воды, при некотором давлении р графически в системе координат р, V некоторой точкой а, имеющей координаты р и vo (рис. 1.11). Если теперь при постоянном давлении р сообщить ей теплоту, то, как показывает опыт, температура ее будет непрерывно повышаться до тех пор, пока она не достигнет температуры кипения f„, соответствующей данному давлению р. Одновременно с этим, как правило, будет увеличиваться и удельный объем от г0 до v' (исключение имеет вода, при нагревании которой от 0 до 4 °С удельный объем уменьшается до минимального, после чего непрерывно увеличивается вплоть до V'). Все параметры кипящей жидкости, кроме давления, будем обозначать одним штрихом. Как показывает опыт, при подводе теплоты к кипящей жидкости происходит постепенное превращение ее в пар. Этот процесс испарения происходит не только при постоянном давлении, но и при постоянной температуре до тех пор, пока последняя частица жидкости не превратится в пар удельного объема V", который называется сухим насыщенным паром (на графике в координатах р, V его состояние обозначено точкой с). Следовательно, Сухим насыщенным паром называется пар, имеющий температуру насыщения при данном давлении а не содержащий жидкой фазы. Впредь все параметры сухого насыщенного пара будем обозначать двумя штрихами. Следует отметить, что вообще насыщенным паром называется пар, находящийся в термическом равновесии с жидкостью, из
которой он получается. Если этот пар не содержит жидкости, то он будет сухим. Насыщенный пар, содержащий в себе капельки жидкости, мы будем называть влажным паром. Таким образом, влажный пар есть смесь двух фаз: жидкой и паровой.
Отрезок изобары Ъ — с отвечает процессу парообразования. Между точками Ь и с имеется смесь жидкости и сухого насыщенного пара. Если считать, что при этом капельки жидкости равномерно распределены в паре, то на указанном участке изобары b — с мы будем иметь влажный пар с изменяющимся содержанием в нем сухого насыщенного пара от х = 0 в точке B до х = 1 в точке с. Эту массовую долю сухого насыщенного пара во влажном паре, обозначенную нами буквой х, называют степенью сухости. Аналогично содержание жидкой фазы во влажном паре называют степенью влажности или влажностью; ее будем обозначать (1 — х). Нетрудно видеть, что при х = О мы будем иметь кипящую жидкость, а при х = 1 — сухой насыщенный пар. Впредь параметры влажного пара будем обозначать индексом «х».
В процессе парообразования удельный объем рабочего тела резко возрастает, поскольку удельный объем сухого насыщенного пара несравненно больше объема кипящей воды. Если к полученному нами сухому насыщенному пару состояния с продолжать подводить при том же давлении р теплоту, то, как показывает опыт, температура его будет увеличиваться, и мы получим перегретый пар некоторого состояния D. Следовательно, перегретым паром называют пар, температура которого больше температуры насыщения TH при данном давлении р < ркР. Впредь все параметры перегретого пара, кроме давления, будем обозначать индексом «пе». Участок с — D на графике в координатах р, V (рис. 1.11) соответствует процессу перегрева пара при постоянном давлении от температуры насыщения до заданной температуры tne, в результате чего удельный объем пара увеличивается от V" до Vne.
Теперь возьмем воду при температуре плавления и при давлении Pi > р. Так как с увеличением давления удельный объем жидкости уменьшается, то точка аь характеризующая состояние жидкости при температуре плавления и давлении рь должна лежать левее точки а. Процесс подогрева жидкости при рх = const на графике в координатах Р, V изобразится отрезком аг — Ьи причем точка Ьх должна лежать правее точки Ь, что объясняется следующим обстоятельством. Для всех жидкостей с увеличением давления повышается температура кипения. Таким образом, с одной стороны, увеличение давления жидкости уменьшает удельный объем ее, но, с другой стороны, с повышением давления увеличивается температура кипящей жидкости, вследствие чего удельный объем ее должен увеличиваться. Как показывает опыт, влияние температуры на повышение удельного объема кипящей жидкости больше, чем давления.
Процесс парообразования при р^ — const изобразится на графике Р, V отрезком Bi — Ci, причем точка сх лежит левее точки с, так как для сухого насыщенного пара воды и подавляющего числа других веществ зависимость V" от р имеет вид Pv'" — const, где т <K.
Рассматривая процесс превращения жидкости в перегретый пар при
постоянном давлении р2 > рь мы получим изобару нагрева жидкости С12 — Ь2, изобару-изотерму испарения ее Ь2 — с2 и изобару перегрева пара C2—D2. Если через точки а, аи а2, ... провести кривую /, то она будет характеризовать состояние жидкости при температуре плавления и различных давлениях. Эта линия является пограничной кривой следующих состояний вещества: слева — двухфазная система лед + жидкость, справа — жидкость. Проведя через точки Ь, Ьь Ь2, ... кривую II, Получим пограничную линию двух состояний вещества: слева — жидкость и. справа — влажный пар. Кривая II характеризует состояние жидкости при температурах кипения и называется пограничной кривой жидкости. Наконец, проведя через точки с, с2, ... кривую III, Получим пограничную кривую двух состояний вещества: слева — влажный пар и справа — перегретый пар. Кривая III характеризует состояние сухого насыщенного пара и называется пограничной кривой пара. Нетрудно видеть, что пограничные кривые жидкости и пара сходятся между собой в точке /с, которая называется критической точкой. Эта точка характеризует критическое состояние вещества, при котором исчезает физическое различие между жидким и газообразным состояниями вещества. Термодинамические параметры вещества при его критическом состоянии называются критическими и обозначаются индексом «к». Согласно новейшим данным, вода имеет следующие значения критических параметров: рк = 22,115 МПа, Тк — 647,27 К, VK = = 0,003147 м3/кг, И к = 2095,2 кДж/кг. Очевидно, критическая температура есть максимально возможная температура жидкости и ее насыщенного пара.
Из рис. 1.11 видно, что с понижением давления кривые I и II Сближаются так, что в точке М они пересекаются. Точка М называется тройной; в ней вещество существует одновременно в трех состояниях: твердом, жидком и газообразном. Каждое вещество в тройной точке имеет присущие только ему значения давления и температуры, например для воды рш = 0,000611 МПа, Тт = 273,16 К и Vm = 0,001 м3/кг.
Параметры состояния жидкости и пара определяются с помощью таблиц, а для насыщенных и перегретых паров — также по /is-диаграмме.
В таблицах насыщенных паров для каждого давления или температуры приведены значения всех термодинамических параметров (кроме внутренней энергии) сухого насыщенного пара и кипящей жидкости. В таблицах перегретых паров для каждого давления при различных температурах приведены значения упе, /іпе и s„e для перегретого пара и некипящей жидкости.
Влажный пар, как двухфазная система, подчиняется закону аддитивности (суммирования) и, следовательно, каждый параметр его Пх можно рассчитать по формуле
Пх = П"х + П'( - х). (1.121)
Из этой формулы можно найти степень сухости пара
X = (Пх - П')/{П" - П'), (1.122)
|
33 |
Если кроме р или T„ задан какой-либо параметр влажного пара 17х.
2 А. В. Чечеткин, Н. А. Занемопец
Из рис. 1.11 видно, что Be/Bc = [Vx — V')/(V" — V') = л'ь Если провести ряд горизонталей Be, BiCГ и т. д. и разделить каждую из них в отношении Be/Bc = Ьіві/ЬіСі = ..., то, соединив все точки плавной кривой, получим линии постоянной степени сухости Xi = Be/Bc. Аналогичным образом получим х2, х3 и т. д. Пограничная кривая жидкости будет х = 0, а пограничная кривая пара — х = 1.
Зависимости р = / (г„) и р = ф (У') или t„ = |/ (V') находятся из опыта.
Зависимость р = / (у") или t„ = ср (и") находится либо экспериментально, либо рассчитывается по известному из курса физической химии уравнению Клапейрона - Клаузиуса, если известна экспериментально найденная зависимость скрытой теплоты парообразования г от температуры.
По решению VI Международной конференции по свойствам водяного пара за начало отсчета внутренней энергии и энтропии принята внутренняя энергия и энтропия жидкой фазы воды в тройной точке, т. е. ит = 0 и Sm = 0. Так как температура в тройной точке у воды и большинства жидкостей близка к температуре плавления, то представляется в химической технологии более целесообразным вести отсчет этих параметров от температуры плавления, т. е. принять м0 = 0 и s0 = 0 при T0 и рт. Тогда H0 = и0 + Pmv0 = P,„V0.
Для воды удельный объем жидкой фазы в тройной точке v„, — = 1 • Ю-3 м3/кг, при t0 = 0°С у0 = 1,0001 • 10"3 м3/кг и, следовательно, К ~ PmV0 = 0,611 Дж/кг йй 0.
У воды при t0 = 0 °С при повышении давления от 0,1 до 10 МПа удельный объем уменьшается только на 0,5 % —с 1,0001-10"3 до 0,9951 • 10"3 м3/кг. Следовательно, воду и другие жидкости практически можно рассматривать как несжимаемые жидкости.
Так как в изобарном процессе нагрева жидкости от Т0 до Т„ теплота жидкости Q' = сртж (Т„ - Т0) = (и' — и0) + P{V' - V0) = и' + Pv' — Pv0, А энтальпия кипящей жидкости H' = и' + Pv', то, очевидно,
H' - Q' + Pv о = Cpm ж (Ті, - Т0) + Pv о, (1.123)
Где Cpmx — средняя изобарная теплоемкость жидкости в интервале температур от Т0 до Тн берется из справочной литературы.
Аналогично, для недогретой до кипения (некипящей) жидкости
H = ср„,ж (Т— Т0) + pv0.
Процесс парообразования есть процесс изобарный, и поэтому энтальпия сухого насыщенного пара будет равна
H" = h' + r, (1.124)
Где г — теплота парообразования, т. е. количество теплоты, необходимое для превращения 1 кг кипящей жидкости (при постоянном давлении) в сухой насыщенный пар.
Теплоту парообразования либо определяют экспериментально, либо рассчитывают по уравнению Клапейрона - Клаузиуса.
Для того чтобы 1 кг сухого насыщенного пара превратить в перегретый пар того же давления и температуры Тпе, необходимо к нему подвести теплоту, равную
<Jne — Cpm (Tirw Ти).
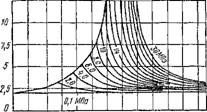
Эту теплоту называют теплотой перегрева. Здесь ерт есть средняя массовая изобарная теплоемкость перегретого пара, которая является сложной функцией давления и температуры. В качестве примера на рис. 1.12 и 1.13 приведена опытная зависимость срт = ф (/>, T) для водяного пара соответственно в до крити ческой и закритической областях давлений.
Очевидно, энтальпию перегретого пара вещества можно рассчитать по формуле
/іпс = H" + = H" + Срт {Тие - Т],). (1.126)
Внутреннюю энергию вещества в любом физическом состоянии будем вычислять через энтальпию по формуле
И — H — pv. (1.127)
|
(1.125) |
Принимая условно энтропию жидкости при температуре плавления s0 = О, впредь вместо изменения энтропии вещества будем говорить об его энтропии в данном состоянии. Тогда энтропия кипящей жидкости (а также некипящей с заменой Тн на Т<Ти):
1 Тн
|
Гт„ |
|
" 5 Q |
|
D Т |
|
-рж |
|
(1.128) |
|
С |
Рт ж In -—;
Энтропия сухого насыщенного пара
|
(1.129) |
|
S' + |
|
5' + |
|
Тп |
Dr_ Тп
И, наконец, энтропия перегретого пара
Гг„
|
Ср dT Т |
|
(1.130) |
S пс = 5 "4"
Обычно при составлении таблиц перегретого пара энтропия подсчи - тывается по формулам, полученным из дифференциальных уравнений термодинамики и опытным данным по теплоемкости ср.
|
П22№р |
||||||
|
WW |
||||||
|
I, |
||||||
|
-400 |
||||||
|
-5005зр |
||||||
|
52^ |
||||||
|
... 1... 1 |
|
Ср, кдж/(кг ас) 32 |
|
300 350 {кр 400 |
|
550 600 T.'c |
|
Рис. 1.13. Зависимость изобарной теплоемкости водяного пара от температуры и давления в закритической области |
|
Ср, кДж/(кг ■ °С)
Too ПО 100 220 260 300 Ж Ш Ш W 500 5W 580 T,°c Рис. 1.12. Зависимость изобарной теплоемкости водяного пара от температуры и давления в докритической области |
|
M m |
|
35 |
2*
|
К |
|
|
|
Рис 1.14. Ts-диаграмма пара |
|
Рис. 1.15. К построению 7$-дмаграммы пара |
|
Т |
Ts-д и а г р ам м а. Как и в случае газов, в термодинамике паров находит широкое применение Ts-диаграмма, в которой площадь под кривой процесса дает количественное выражение теплоты процесса. На рис. 1.14 в системе координат Т, s представлен изобарный процесс превращения 1 кг воды при температуре плавления в перегретый пар заданной температуры перегрева, соответствующей состоянию в точке D. Кривая ab представляет изобарный процесс нагрева воды от Т0 = = 273 К до Тн при данном давлении р; поэтому площадь под кривой процесса будет представлять q'. В процессе подогрева жидкости зависимость s = ф (Т) выражается уравнением (1.128), откуда следует, что кривая ab в первом приближении есть логарифмическая линия. Площадь под кривой be есть теплота парообразования г. В соответствии с уравнением sx = s"x + s' (1 — х) = s' + гх/Ти в процессе парообразования sx — s' — rx/TH и, следовательно, площадь под прямой be есть гх. Очевидно, площадь под кривой cd есть теплота перегрева <jnc. Процесс перегрева описывается уравнением (1.130), которое приближенно можно представить в виде sne — s" яз Cpm In (TnJTH). Следовательно, в первом приближении линия cd есть логарифмическая кривая. Так как для воды СрЖ > ср, то кривая перегрева пара cd идет круче кривой нагрева воды Ab. Степень сухости влажного пара давлением р в точке е определится как отношение отрезков be к be, так как be: be = (rx/TH): (r/Tn) = x. Как видно из рис. 1.14, 1.15, при увеличении давления точки b и с, оставаясь в каждом отдельном случае на горизонтали, сближаются и при критическом давлении сливаются в одну точку к. Соединив между собой точки bi, b2, b2 и т. д., соответствующие состоянию кипящей жидкости при различных давлениях, получим пограничную кривую жидкости х = 0. Аналогичным образом получим пограничную кривую пара х = 1, соединив между собой точки с, Сі, С2 и т. д., соответствующие состоянию сухого насыщенного пара при различных давлениях. Подобно пограничным линиям ри-диаграммы, пограничная кривая
жидкости на Ts-диаграмме разделяет область существования жидкого состояния вещества (слева от нее) от области влажных паров его (справа от кривой). Аналогично, пограничная кривая пара на Ts- Диаграмме разделяет область влажных паров (слева от нее) от области существования перегретого пара (справа от кривой).
Построим Ts'-диаграмму для водяных паров. Чтобы определить характер кривых изобар, найдем значения (dT/ds)p = tg Ар для изобары и (dT/ds)v = tg а„ для изохоры. Так как s — функция состояния, то ds — есть полный дифференциал, и, следовательно, можно написать, что
|
|
(1.131)
(1.132)
|
Сравнивая уравнение (1.131) с уравнением (1.80), а (1.132) с (1.76), получим соответственно:
|
|
(1.133) |
|
|
(1.134)
Где Ир и <ха — углы наклона касательной к изобаре и изохоре соответственно. Для воды срж я* £'11Ж и, следовательно, в соответствии с уравнениями (1.133) и (1.134) изохора нагрева воды практически совпадает с изобарой. В настоящее время установлено, что изобара нагрева воды практически совпадает с пограничной кривой жидкости х — 0. Следовательно, для воды в первом приближении пограничная кривая жидкости одновременно является и изохорой нагрева жидкости (рис. 1.15). Так как процесс парообразования является одновременно процессом и изобарным и изотермическим, то в области влажного пара изобары Be, B'C', B"C" и т. д. есть прямые, параллельные оси Os (рис. 1.15). В изо - хорном процессе подвод к влажному пару теплоты, а следовательно, и увеличение энтропии приводит к увеличению его давления и температуры; следовательно, (dT/ds)Vt Х = tg а„, * > 0, т. е. изохорная теплоемкость влажного пара положительна. Конкретный вид изохоры в области влажного пара дан на рис. 1.15.
Для воды (дТ/дх)х=і <0, следовательно, в соответствии с уравнением (1.133) с = сх=1 = T(ds/dT)x= і < 0, т. е. теплоемкость сухого насыщенного пара воды отрицательная. Это значит, что при нагревании этого пара теплота будет не поглощаться, а выделяться. Как видно из рис. 1.15, угол наклона касательной к пограничной кривой пара х= 1 изменяется в диапазоне от 90 до 180°, т. е. с#=ь оставаясь все время величиной отрицательной, в критической точке равна минус бесконечности. Для всех веществ в критической точке ск = — оо, а так как сх=1 есть непрерывная функция температуры, то, следовательно, для всех веществ вблизи критической точки теплоемкость сухого насыщенного пара отрицательна. Однако есть вещества, как, например, дифенилоксид (рис. 1.16), у которых при невысоких температурах насыщения сл=і > 0; с повышением Тп она убывает, становится равной нулю (при а — 90°), затем принимает отрицательное значение, возрастая до —оо в критической точке.
|
5 Рис. 1.16. 7s-диаграмма паров дифенилоксида |
|
Т |
|
О |
|
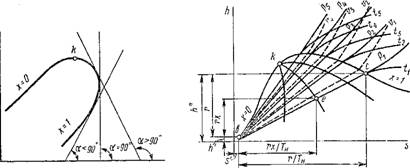
Рис. 1.17. /^-диаграмма паров |
Изобарная и изохорная теплоемкости перегретого пара — положительные и, следовательно, изобары и изохоры в области перегретого пара в первом приближении есть логарифмические линии, поднимающиеся вверх с увеличением энтропии. Так как ср > cv, то изохоры идут круче изобар. Изоэнтропы на Ts-диаграмме есть прямые, параллельные оси ОТ, а изотермы — прямые, параллельные оси Os.
Hs-дИаграмма. Одним из основных достоинств этой диаграммы (рис. 1.17) является то, что в ней теплоты жидкости, парообразования и перегрева пара в изобарном процессе изображаются прямолинейными отрезками. Пограничные кривые строятся по точкам h' и s' — для кривой х = 0 и по точкам h" и s" — для кривой х = 1. Значения этих величин берутся из таблиц сухого насыщенного пара. Так как для изобарного процесса ds = dQp/T= dh/T, то (Dh/ds)p = T= tg ap > 0, или а. р < 90°. Отсюда следует, что на /is-диаграмме изобары представляют собой восходящие кривые (сплошные линии). Чем больше давление, тем выше располагается соответствующая изобара. В области влажного пара Т= Тх = Ти = const, и, следовательно, ар = const, т. е. в этой области изобары — прямые линии. Как видно из рис. 1.17, отношение Ъе:Ъс = (гх/Т„):(Г/Тп) = х. Соединив кривой все точки на изобарах с одинаковым значением степени сухости х, получим линии постоянной степени сухости х = const.
В области влажного пара по указанной выше причине изотермы совпадают с изобарами. В этой области длина прямолинейного участка изотерм уменьшается с увеличением Т и при Т = Тк обращается в точку. Следовательно, в критической точке (dh/ds)j — Тк > 0 и поэтому критическая точка к находится на нисходящей части пограничной кривой пара х = 1. От пограничной кривой пара х = 1 изотермы резко поворачивают вправо и при больших степенях перегрева идут практически параллельно оси Os, т. е. изотермический процесс становится одновременно изоэнтальпийным, что характерно для идеального газа (dh/ds)T = (с,, dT/ds)r ~ tg а г = 0, т. е. а г = 0. Вблизи кривой насыщения (х = 1) tgccr>0, и в этой области изотермы представляют собой кривые выпуклостью вверх. Чем больше температура, тем выше располагается соответствующая изотерма.
В /is-диаграмме изохоры изображаются пунктирными кривыми с Tg OlV — (Dh/Ds)V > 0. Чем больше удельный объем пара, тем ниже располагается соответствующая изохора.
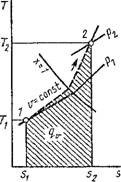
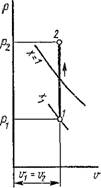
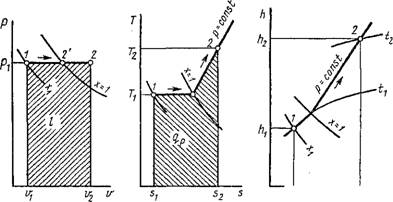
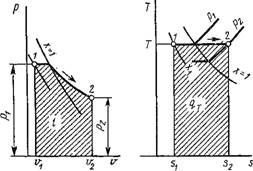
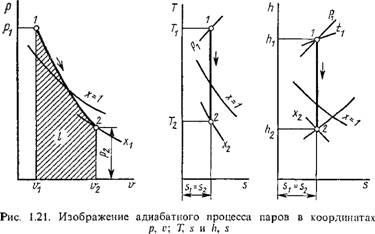
Термодинамические процессы в парах. Обычно рассматриваются четыре процесса: изобарный (р = const), изохорньгй (и = const), изотермический (Т = const) и изоэнтропийный, или обратимый адиабатный (s = const). На рис. 1.18 изображен изобарный процесс, на рис. 1.19 — изохорный, на рис. 1.20 — изотермический и на рис. 1.21 — адиабатный.
|
Т, s И h. s
|
|
|
Термодинамические параметры состояния в начале и конце этих процессов находятся или непосредственно из /is-диаграммы, или из таблиц сухого насыщенного и перегретого пара. Во втором случае необходимо прежде всего определить состояние рабочего тела в начале и в конце процесса. Для изобарного, из ох орного и изотермического процессов эти состояния определяются путем сравнения заданного
|
|
|
S/ |
'z s |
|
|
В координатах р, V |
||
|
H |
Y |
|
|
І/ |
Ь |
|
|
N |
Z4J |
|
|
Л |
[4 7 |
Рис. 1.19. Изображение изохорного процесса паров в Координатах р, v;
Т, S И h, s
|
|
|
Рис 1.20. Изображение изотермического процесса паров в координатах р, V; Т, s И h, s
|
Удельного объема v с удельными объемами сухого насыщенного пара и кипящей жидкости при заданной температуре или давлении. При этом возможны следующие случаи: 1) если V > V", то пар — перегретый и все остальные параметры его берутся из таблиц перегретого пара для заданного р или t; 2) если v = v", то пар — сухой насыщенный и все параметры его берутся из таблиц сухого насыщенного пара для заданного р или г; 3) если V = V то задана кипящая жидкость и все параметры ее берутся из таблиц сухого насыщенного пара при заданном Р или f; 4) если Vq < v < v', то задана некипящая жидкость и все параметры ее берутся из таблиц перегретого пара (выше горизонтальной черты); 5) если v' < v < v", то пар — влажный; степень сухости его определится из формулы (1.122), а энтальпия и энтропия — из формулы (1.121), причем входящие в эти формулы параметры пара и жидкости берутся из таблиц сухого насыщенного пара при заданном р или t.
|
|
Для адиабатного процесса состояние рабочего тела в начале процесса определяется аналогичным образом; в конце же процесса — путем
сравнения известной энтропии s2 = «і с энтропией сухого насыщенного пара и кипящей жидкости заданного давления р2 или температуры t2, При этом возможны те же пять случаев, а именно: если s2 > s2> то пар перегретый, если s2 — s2, то пар сухой насыщенный, если s2 — S'2, То это кипящая жидкость, если s0 < s < s то это некипящая жидкость, и, наконец, если s' < s < s", то пар влажный. Определив состояние пара в конце и начале адиабатного процесса, все параметры состояния находятся так же, как в указанных выше трех процессах.
Изменение внутренней энергии, теплоту процесса и работу рассчитывают так же, как и для реальных газов, не подчиняющихся уравнению Менделеева — Клапейрона.

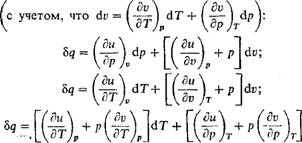
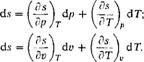
 Опубликовано в
Опубликовано в