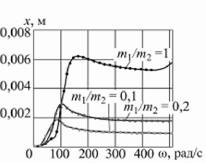
Анализ установившихся режимов колебаний проводился при различных значениях постоянного напряжения пи­тания U0. На низковольтных режимах U0=1 В при малых средних угловых ско­ростях ю = 35-50 рад/с колебания рабоче­го органа носят выраженный полигармо­нический характер (рис. 3), что связано с наличием гармонических составляющих в угловой скорости вращения дебаланса.

Возникновение колебаний в угловой скорости обусловлено переменностью момента дебаланса относительно оси его вращения в поле силы тяжести и колеба­ниями самой оси вращения. При этом чем больше относительная масса дебаланса, тем больше оказывается амплитуда гар­монических составляющих в законе изме­нения угловой скорости и, соответствен­но, в законе колебаний рабочего органа. Точно так же влияет и технологическая нагрузка от взаимодействия с обрабаты­ваемой средой: по сравнению со случаем, когда сила F3=0, амплитуды дополни­тельных гармоник увеличиваются.

Л", м_

	Л	1		Г
					Vy-
			1

0,0002

-0,0002

-0.0004

V, l"

1,7 1,{! 1,4 Рис. 3. Перемещение рабочего органа при m1/m2=0.2, U0=1 В

С ростом напряжения питания сред­няя угловая скорость вращения дебаланса монотонно увеличивается (рис. 4 а, б). При этом оказалось, что значение сум­марной силы вязкого трения незна­чительно влияет на характер зависимости

Ю(и0).

С повышением напряжения питания средняя угловая скорость возрастает, и по мере приближения к области резонанса закон колебаний рабочего органа при­ближается к гармоническому, а амплиту­да его колебаний увеличивается.

При достижении напряжении пита­ния значения U0=12 В и выходе системы в зарезонансную область колебаний дви­жение рабочего органа становится почти гармоническим, несмотря на полигармо­нический характер изменения угловой скорости ф, что вызвано увеличением влияния колебаний оси дебаланса.

Частотные зависимости амплитуды колебаний рабочего органа Х(ю) приве­дены на рис. 4 в, г.

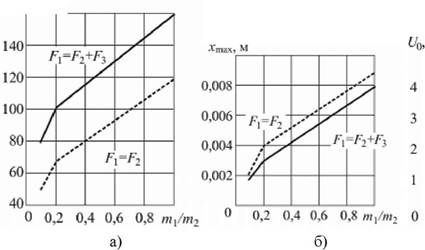
С увеличением относительной массы дебаланса mj / m2 резонансная амплитуда Xmax и частота Qres увеличиваются (рис. 5, а и б); при этом для поддержания резо-

		1 Т^/т-х
	Т	Jm2	=0j2_
				' 1 Ш(	'п>2-
		F

400 300 200 100 0

2 4 6 8 10 а)

Нансных колебаний подаваемое напряже­ние U0 должно быть больше (рис. 5, в). Увеличение резонансной амплитуды свя - ш, рад/с 500

Зано с ростом силы инерционного возбу­ждения при уменьшении массы рабочего Органа. ш, рад/с 500

,= 1

Ц>,

		Т1/т2 і	"0,2
	Ffl]/	Т2 =	0,1
				ТП]А	«2=1

400 300 200 100 о

2 4 6 8 Uih В Б)

			ПЛ/т	2-І
		/т-, It	- п 1
	4	—1—	= 0,2

0 100 200 300 400 рад/с

Г, м 0,01

0,008 0,006 0,004 0,002

В) Г)

0>rt,4, Рад/с

Рис. 5. Зависимости резонансной частоты Qres (а) и резонансной амплитуды Xmax (б) Колебаний рабочего органа и подаваемого напряжения U0 (в) от относительной массы дебаланса m1/m2: 1 - F1=F2; 2 - F1=F2+F3

Рис. 4. Зависимости средней угловой скорости вращения дебаланса от напряжения: а - Fj = F2, б - Fj = F2 + F3, амплитудно-частотные характеристики системы: в - Fj = F2, г - Fj = F2 + F3

-/'і		F-
	У	* У
/	У	У'	'' Л
#'

0,2 0S4 0,6 m{/m2 В)

Упруго-вязко-пластическое взаимо­действие инструмента с обрабатываемой средой (случай F = F2 + F3), по сравне­нию с упруго-вязким (случай Fj = F2),

Приводит к увеличению резонансной час­тоты (см. рис. 5, а) и уменьшению резо­нансной амплитуды (см. рис. 5, б). Резо­нанс при меньших напряжениях без дей­ствия упругопластической силы F3 техно­логической нагрузки объясняется отсутст­вием потерь энергии на сухое трение, спад АЧХ в этом случае менее пологий.

В зарезонансной области увеличение относительной массы дебаланса приводит к уменьшению амплитуды колебаний ра­бочего органа, которая оказалась практи­чески не зависящей от действия техноло­гической нагрузки.

Заключение

В работе была рассмотрена динами­ка виброинструмента, оснащенного деба - лансным электроприводом, рабочий ор­ган которого взаимодействует с обраба­тываемой средой.

Результаты численного интегриро­вания нелинейных дифференциальных уравнений позволили проанализировать стационарное движение рабочего органа и влияние на движение свойств электро­привода и параметров модели технологи­ческой нагрузки.

Установлено, что при малых коэф­фициентах вязкости и небольшой относи­тельной массе дебаланса влияние техно­логической нагрузки проявляется в немо­нотонном характере изменения средней мощности от средней скорости вращения в виде резонансного пика, а при зна­чительных массах дебаланса происходит сглаживание резонансного пика.