Арифметические инструкции
 8 января, 2013
8 января, 2013  admin
admin На языке СПД ЧПУ можно описывать различные вычислительные операции. Для вычислительной операции составляется арифметическое выражение, состоящее из скалярных констант, скалярных переменных и стандартных функций, объединенных арифметическими операторами.
О скалярных константах и скалярных переменных говорилось выше. Стандартные функции задаются идентификатором функции, определяемым служебным словом языка, и аргументом, находящимся за ним в скобках. Стандартные функции включают арифметические и геометрические функции: SINF — тригонометрический синус; COSF — тригонометрический косинус; TANF — тригонометрический тангенс; SQRTF — квадратный корень; ATANF — арктангенс; ABSF — абсолютная величина.
Аргументы тригонометрических функций должны выражаться в градусах, десятичным числом, содержащим целую и дробную части.
Так, запись В =20*SINF(30.5) означает, что скалярной переменной, обозначенной идентификатором В, присвоено значение, равное произведению числа 20 на синус угла 30°30'.
Аргументы функций могут быть заданы скалярными константами и скалярными переменными, значения которых определены предварительно, а также любым допустимым арифметическим выражением, например:
ALF=ATAN(45.3-20.8)*COSF(23.35)/ 28.44
DELT=56.8*SINF(ALF)
Здесь предварительно определено значение скалярной переменной ALF как значение арктангенса, аргументом которого является конкретное арифметическое выражение. Затем ALF используется как аргумент функции синуса в арифметическом выражении для определения скалярной переменной DELT.
Большое практическое значение имеют геометрические функции как функции извлечения канонических форм из ранее установленных геометрических элементов (особенно из предварительно найденных точек): XGEOF, YGEOF, ZGEOF. Точка определена, если известны ее координаты по всем осям, т. е. х, у, г.
Допустим, Р15 — идентификатор ранее найденной точки. Тогда выражения
A=XGEOF(P15),B=YGEOF(P15), C=ZGEOF(P15)
Свидетельствуют о том, что скалярной переменной, обозначенной идентификатором А, присваивается значение, равное по величине значению координаты х точки, обозначенной идентификатором Р15. Аналогично определяются другие скалярные переменные (В, С), с той лишь разницей, что их значения будут равны соответствующим координатам точки Р15 по осям Y и Z.
Отсюда видно, что аргументом геометрической функции может быть только идентификатор геометрической переменной.
|
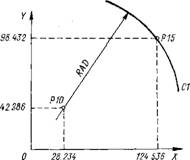
Рис. 10.18. Определение радиуса окружности |
Пример. Вариант практического использования геометрических функций. Допустим, имеются две точки (рис. 10.18): РЮ (28.234, 42.286) и Р15 (124.536, 98.432). Необходимо провести окружность С1, центром которой будет точка РЮ, при этом окружность должна пройти через точку Р15. Для определения >» окружности необходимо знать координаты центра и радиус. Координатами центра С1 являются координаты точки РЮ, радиус R — = (Дх2 + Ду2)|/2. В СПД радиус можно найти следующим образом:
RAD=SQRTF((XGEOF(PI5)-XGEOF(PI0)* (XGEOF(PI5)-XGEOF(P10))+(YGEOF(PI5) - YGEOF(PIO))*(YGEOF(P15)-YGEOF(P10))) CI=CIRCLE/CENTER,P10,RADIOS,BAD
Здесь RAD — идентификатор скалярной переменной, соответствующий радиусу окружности С1.
Из приведенного примера видно, что СПД ЧПУ обладает довольно широкими возможностями для выполнения различных вспомогательных расчетов, которые в других аналогичных системах автоматического программирования осуществляются вне вычислительного процесса на ЭВМ.

 Опубликовано в
Опубликовано в