Плоское контурное фрезерование
 6 января, 2013
6 января, 2013  admin
admin В практике наибольшее применение находит плоское контурное фрезерование, обеспечивающее обработку деталей, контур которых состоит из отрезков пря-
|
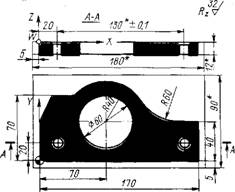
Рис. 8.18. Деталь типа «крышка» в системе координат детали |
Мых и дуг окружностей. При составлении РТК и определении координат опорных точек траектории движения центра фрезы при обработке деталей фрезерованием обычно исходят из эквидистантного характера траектории. В соответствии с этим на РТК указывают обрабатываемый контур и эквидистантную ему траекторию движения инструмента с опорными точками. Естественно, определить координаты опорных точек эквидистанты более просто, если известны координаты всех опорных точек контура детали. Эти последние удобнее всего задавать в системе координат детали в виде таблицы (табл. 8.3).
|
Таблица 8.3. Координаты опорных точек контура обрабатываемой детали
|
Рассмотрим деталь (рис. 8.18), в которой предполагается фрезерование контура фрезой с радиусом /?„ = 10 мм и расфрезеровка отверстия диаметром 60 мм (траектория движения фрезы — от центра к окружности). Для захода фрезы в центре выполнено отверстие диаметром 22 мм.
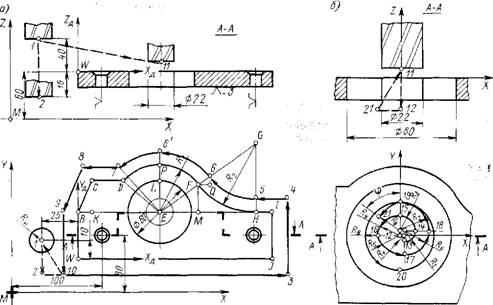
Координаты опорных точек эквидистанты (рис. 8.19, а) могут быть рассчитаны в соответствии с определенными методиками [15], кратко изложенными в гл. 7. Числовые значения координат представлены в табл. 8.4.
|
Рис. 8.19. Схема построения траектории движения фрезы при обработке детали типа «крышка»: » а — при обработке контура; б — при обработке отверстия |
Траектория фрезы при обработке отверстия диаметром 60 мм построена по принципу четырехполюсной спирали для окружности радиусом R, = 20 мм и диаметра фрезы £>фр =
|
Таблиц а 8.4. Координаты опорных точек эквидистанты (траектории движения центра инструмента) при обработке детали типа «крышка»
|
|
1 |
-25 |
10 |
40 |
|
2 |
-25 |
-10 |
— 16 |
|
3 |
180 |
-10 |
— 16 |
|
4 |
180 |
50 |
-16 |
|
5 |
150 |
70 |
-16 |
|
6 |
110 |
80 |
-16 |
|
7 |
40 |
80 |
— 16 |
|
8 |
8,77 |
80 |
-16 |
|
9 |
-10 |
42,36 |
-16 |
|
10 |
-10 |
-10 |
-16 |
|
11 |
70 |
40 |
5 |
|
12 |
70 |
40 |
— 16 |
|
= 2R„ = 20 мм (рис. 8.19,6). Шаг спирали определен из условия h = R3/a = 20/2=10 мм, где число витков спирали а = 2 выбрано как большее целое нижнего предела множества чисел, удовлетворяющих условию |
RЭ ^ 20 _|67 > R, = 0,60фр 0,6-20 ' 0,8Дфр
Сторона четырехполюсника B=H/A = = 10/4 = 2,5 мм.
Координаты начальных точек (хи, у„) И центров (Хи, уи) дуг окружностей участков спирали, вычисленные в местной системе координат X, У, а также радиусы R этих дуг окружностей приведены в табл. 8.5.
Фрезу от контура обратного отверстия отводят по дуге окружности радиуса RB = 17,5 мм с центром в полюсе (хц = 0; уц = 2,5 мм) до точки 21, определенной углом ф = 45°. Координаты точки 21:
*2i = х„— RВ sin ф = 0— 17,5 sin 45° =
= — 12,37 мм;
Y2i=ya + RB cos ф = 2,5+ 17,5 cos 45° =
= 14,87 мм.
|
Таблица 8.5. Координаты опорных точек траектории «четырехполюсная спираль»
|
|
12—13 |
0 |
0 |
2,5 |
0 |
2,5 |
|
13—14 |
2,5 |
— 2,5 |
2,5 |
0 |
5,0 |
|
14—15 |
7,5 |
2,5 |
0 |
2,5 |
7,5 |
|
15—16 |
0 |
10,0 |
0 |
0 |
10,5 |
|
16—17 |
-10,0 |
0 |
2,5 |
0 |
12,5 |
|
17—18 |
2,5 |
-12,5 |
2,5 |
2,5 |
15,0 |
|
18—19 |
17,5 |
2,5 |
0 |
2,5 |
17,5 |
|
19—20—19 |
0 |
20,0 |
0 |
0 |
20,0 |

 Опубликовано в
Опубликовано в