ОСОБЕННОСТИ РАСЧЕТА ТРАЕКТОРИИ ИНСТРУМЕНТА
 3 января, 2013
3 января, 2013  admin
admin
Расчет траектории инструмента при ручном программировании состоит прежде всего в определении координат опорных точек на контуре детали и (если траектория является эквидистантной к обрабатываемому контуру) на эквидис - танте. При этом предполагается (см. гл. 1), что принятую траекторию, фиксированную опорными точками, при обработке последовательно обходит центр инструмента.
При расчете траектории инструмента уточняют параметры резания (скорость резания и подачу) на отдельных участках траектории.
Расчет координат опорных точек на контуре детали. Начальный этап расчета— определение координат опорных точек контура детали в выбранной системе координат. Для этого используют заданные на чертеже деталей размеры и данные РТК - Координаты опорных точек контура детали вычисляют с помощью уравнений, описывающих геометрические элементы контура детали, и соотношений в треугольниках. Точность вычислений обычно ограничивается дискретностью задания перемещений, определяемой конкретной схемой УЧПУ и используемым станком.
Наиболее часто в процессе программирования контурной обработки решаются задачи определения координат опорных точек, лежащих на прямых, окружностях и пересечениях этих элементов.
Прямые линии описываются уравнением Y = Kx--By представление которого зависит от исходных данных. В уравнении прямой K — угловой коэффициент, рав-
|
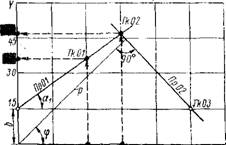
0 15 Ш Ш во 75 X Рис. 7.3. К определению параметров прямой |
Ный тангенсу угла наклона прямой к оси абсцисс; 6 — начальная ордината, равная ординате точки пересечения прямой с осью ординат (рис. 7.3).
Например, при начальной ординате й=15 мм и угле oci=35° уравнение прямой (ПрО 1) будет иметь вид
У = /ex + ft = х tg 35° + 15 = 0,7х + 15.
Пользуясь этим уравнением, нетрудно для любой точки прямой определить одну координату по заданной другой.
Например, при известной абсциссе х, — = 30 мм ордината точки Тк01 будет у — = 0,7-30+15 = 36 мм. При хг = 45 мм ордината уг = 0,7-45+ 15 = 46,5 мм.
При известных координатах одной точки (хт, г/т) и угле наклона прямой уравнение этой прямой имеет вид
Y = K(X — Хт) +уг.
Если координаты точки Тк02 хг = 45 мм и Уг = 46,5 мм, а угол ai=35°, то уравнение прямой Пр01
Y = k(x — x-i) +i/2 = tg 35°(х— 45) +
+ 46,5 == 0,7л - -0,7-45 + 46,5 = 0,7х + 15.
|
У2 — У1 Л'2 — Х| |
Уравнение прямой, проходящей через две заданные точки Тк01 (х, уI) и Тк02 (Х2, У2), записывается в виде
(X — Xi) + у,.
При Тк01 (30; 35) и Тк02 (45; 46,5) уравнение прямой Пр01 примет вид
46,5-36
(х— 30) +36 =
75-30
= 0,7 (х— 30) +36 = 0,7х + 15.
Уравнение прямой Пр02 при известных точках Тк02 (45; 46,5) и ТкОЗ (75; 15)
15-46,5
(х — 45) +46,5 =
75-45
= — 1,05 (х — 45) + 46,5 = — 1,05* + 93,75.
Уравнение прямой при необходимости можно выразить полярным расстоянием р (перпендикуляр из начала координат к прямой) и полярным углом ф (угол между перпендикуляром и осью абсцисс):
Х cos Ф + у sin ф —р=0.
При р = 64,58 мм и ср = 43,55° уравнение прямой Г1р02
Х cos 43,55° +у sin 43,55° —64,58 = 0.
После подстановки значений тригонометрических функций это уравнение приводится к уравнению прямой в общем виде:
0,7247х + 0,6889;/ — 64,58 = 0,
Или
0,7247 , 64.58 - х + -
0,6889 ^ 0,6889 '
Или
У= — 1,05* +93,75.
Точка пересечения двух прямых определяется решением системы уравнений, описывающих эти прямые. Решением системы уравнений
Y = K)X--Bi 1/ = &2Х+Й2 '
Являются координаты точки пересечения:
XT=(b2-b,)/(fel-fe2); Ут = K[XT-- Ь.
Так, для прямых Пр01 и Пр02 (см. рис. 7.3), уравнения которых
У = 0,7х+15; у= — 1,05л:+ 93,75,
Координаты общей точки Тк02:
X2=(b, — bi)/(kx—ki) = (93,75- -15)/(0,7+1,05) =45 мм;
1/2 = 0,7х+ 15 = 0,7-45+ 15 = 46,5 мм.
Уравнение окружности радиусом R с центром 0(х о, у о) имеет вид
/?= (х-х0)2 + (у — уо)'2,
Или, когда оно разрешено относительно ординаты,
|
У = |
У = Уо± [Л2— (х —х0)2] '/2.
Точке на окружности, заданной абсциссой хт, соответствуют два (точки Тк04 и Тк04') значения ординаты:
Гл = 1/о± [tf2-(xT-xо)2]""2,
А точке, заданной ординатой ут — два значения абсциссы: - .
Хт = х0 + [^-(^-уо)2]1/*.
Требуемое решение выбирают из этих значений по признаку расположения искомой точки.
Если выражение в квадратных скобках равно нулю, что имеет место при задании предельных значений одной из координат, то другая координата точки определяется однозначно.
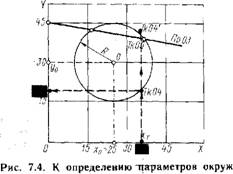
Например, окружность радиуса R = 15 мм с центром О(хо = 25 мм; уо = 30 мм) описывается (рис. 7.4) уравнением
У = Уо± !R2- (Х — Хо)2] 1/2 = 30 + [152-
— (х —25)2]1/2. и:
Ордината Тк04 при заданной абсциссе *4 = 35 мм
У = 30+ [152- (35-25)2]1/2 = 30+ 11,18.
Искомая ордината соответствует меньшему из двух ее возможных значений: у = 30-г - -11,18=18,82 мм.
Точки пересечения прямой и окружности определяются решением системы описывающих их уравнений. Решение системы уравнений прямой и окружности, а также двух окружностей, приводит к выражению вида
Х = а+ [...]1/2,
Где величина в квадратных скобках может быть больше, равна или меньше нуля; соответственно точек пересечения будет две, одна (элементы касаются) или ни одной (элементы не пересекаются).
Так, окружность (рис. 7.4) с радиусом R = 15 мм, с центром О (х0 = 25 мм; уо = 30 мм) описывается уравнением
У = 30± [152— (х — 25)2]1/2, прямая ПрОЗ — уравнением
У= —0,14х + 45.
Решение системы этих уравнений позволяет определить координаты точек Тк05 и Тк04:
-0,14х + 45 = 30 + [ 152 — (х — 25)2] 1/2,
|
Ности |
Или 15 — 0,14х = + [152 — (х — 25)2] 1 /2, или (15 — 0,14х) 2 = 152 — (х —25)2, или х2 —53,158х + 612,985 = 0;
Х-2=—р/2± [ (р/2)2 — Q]1/2 = 26,579 +
+ (706,443 —612,985)1/2 = 26,579 + 9,667.
Искомые координаты точек пересечения:
Х5 = 36,246; Хб= 16,912;
Уъ = — 0,14xi + 45 = — 0,14 • 36,246 + 45 =
= 39,92;
Уе= —0,14x2 + 45= — 0,14 • 16,912 + 45 =
= 42,63.
Совместным решением уравнений можно также достаточно просто определить точки пересечения двух окружностей, точки касания прямой с одной и двумя окружностями, а также точку касания двух окружностей и т. д. [15, 28].
Расчет координат опорных точек на эквидистанте. Координаты опорных точек эквидистантной траектории инструмента наиболее просто представить как приращение координат опорных точек контура детали. Целесообразность предварительного определения опорных точек контура очевидна, поскольку в плоскости обработки в большинстве случаев траектория центра инструмента представляет собой линию, эквидистантную обрабатываемому контуру.
Эквидистанта как геометрическое место точек, равноудаленных от контура детали на расстояние, равное радиусу Rи инструмента, строится справа или слева от элементов этого контура в зависимости от расположения инструмента
275
|
А)
|
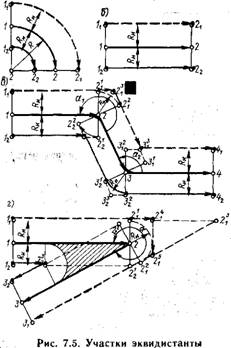
Относительно обрабатываемого контура. Эквидистантой к дуге окружности 1—2 является дуга концентричной ей окружности /1—21 или h—2ч с тем же центральным углом (рис. 7.5, а), а к отрезку прямой 1—2 — отрезок, параллельный данному (рис. 7.5,6).
Метод соединения элементов эквидис - танты выбирают в зависимости от угла а, образованного соседними элементами контура, если смотреть со стороны расположения инструмента при обходе этого контура (рис. 7.5, в, г). Этот угол для пары отрезков измеряют непосредственно между ними. Если же элементом контура является дуга окружности, то угол а измеряют относительно касательной к этой дуге в общей точке рассматриваемой пары элементов контура детали. Так, при а> 180° элементы эквидистанты соединяются сопрягающими дугами окружностей радиусом RH, центры которых находятся в общих точках элементов контура. При а<180° общей точкой элементов эквидистанты является точка пересечения этих элементов (рис. 7.5, в).
Для сопряженных элементов контура (а = 180°) элементы эквидистанты также сопряжены.
Движение центра инструмента вдоль сопрягающей дуги окружности эквидистанты при обработке острого угла контура может привести к «зарезам» из-за изменения величин и направлений сил резания. В этом случае более технологичной является траектория центра инструмента, в которой дуги сопрягающих окружностей заменены отрезками прямых, продолжающих участки эквидистанты к элементам контура. Для случая, приведенного на рис. 7.5, в, левой эквидистантой является линия h—2—2— <??—41, а более технологичной траекторией—линия 1—23(А)—Зъ—4.
При обходе углов а> 300° во избежание значительных отклонений траектории инструмента от эквидистанты необходимо сделать дополнительные построения. Примером может служить перпендикуляр, опущенный из точки 2 (рис. 7.5, г). Поэтому для рассматриваемого случая левой эквидистантой будет линия U— 2F—2F—3, или /,— 2?—3,.
При вычислении опорных точек эквидистанты различают три типовых случая сопряжения дугой (радиусом Rи) участков эквидистанты: прямая — прямая, прямая — окружность и окружность — окружность (табл. 7.2). Как уже говорилось, координаты опорных точек траектории инструмента чаще всего рассчитывают путем определения приращений координат опорных точек контура детали. Для нахождения этих приращений существуют определенные зависимости. Возможны и другие схемы расчета [15].
Трудоемкость вычисления координат опорных точек•при ручном программировании во многом зависит от опыта технолога-программиста, его знаний и способности ориентироваться при постановке и решении геометрических задач. Систематизация встречающихся геометрических задач и способов их решения не исключает индивидуального подхода к конкретной задаче, что часто позволяет найти более простое ее решение. Ускоряет решение задач и использование справочной литературы, содержащей типовые
|
Схема |
Примеры геометрических построений [28, 48, 57].
Особенности расчета с использованием ЭВМ. Трудоемкость процесса определения координат опорных точек существенно снижается при использовании микроЭВМ. Такие ЭВМ имеют математическое обеспечение в виде минимальных систем подготовки УП. Язык системы содержит ограниченное число вычислительных процедур и позволяет решать задачи по определению точек стыков геометрических элементов траектории перемещения центра инструмента. Обычно исходные данные в такие микроЭВМ вводят через клавиатуру печатающего устройства или дисплея.
При использовании микроЭВМ можно также решать ряд других. задач, например рассчитывать частоты вращения шпинделя на каждом переходе при заданной скорости, находить максимально допустимый крутящий момент, определять скорости подачи по контуру и др. Достаточно прост при этом вывод рассчитываемой траектории на графопостроитель, что позволяет более четко контролировать разрабатываемую УП.
При программировании токарной обработки составляют РТК. При составлении РТК учитывают типовые схемы обработки отдельных элементов детали и определяют траектории всех инструментов, назначенных для выполнения операции.
Программирование обработки винтовых поверхностей. Крепежные и ходовые. резьбы, червяки, шнеки и другие винто - ; вые поверхности могут обрабатываться на станках с ЧПУ, имеющих связь между поступательным и вращательным движениями рабочих органов. Эта связь, в отличие от жесткой механической связи на токарно-винторезных станках с ручным управлением, осуществляется синхронизацией движения подачи с вращением шпинделя с помощью установленного на нем датчика углового положения.
Принципиально на станках с ЧПУ могут быть реализованы разнообразные схемы перемещения инструмента для нарезания одно - и многозаходных цилиндрических и конических резьб, а также винтов различного профиля с постоянными или изменяющимися по заданному закону шагами винтовых поверхностей.

 Опубликовано в
Опубликовано в