Многие реальные структурно-неоднородные (много­фазные) тела не обладают каким-либо одним механиче­ским свойством. Процесс деформирования их сложен и в ряде случаев не может быть описан уравнениями гид­родинамики или теории упругости, так как по своим де - формативным характеристикам структурно-неоднород­ные тела занимают некоторое промежуточное положение между вязкими жидкостями и реальными твёрдыми те­лами.

Такие сложные системы характеризуются реологиче­скими свойствами. Для. их изучения используются ме­ханические модели, адекватные реальным телам. По­добные модели могут состоять из упругих пружин, гид­равлических амортизаторов трущихся элементов, кото­рые, вообще говоря, не имеют точных аналогов в реаль­ных материалах.

Три основные свойства материалов — упругость, вяз­кость и пластичность — могут быть представлены сле­дующими механическими моделями: упругость (тело Гу - ка — Н) изображается спиральной пружиной, а ньюто­новская жидкость — моделью (N) в виде пробирки, на - - полненной очень вязким маслом, в котором перемещает­ся поршень. Пластическое твёрдое тело можно предста­вить моделью Сен-Венана (st. У), состоящей из груза, с шероховатой поверхностью, соприкасающейся с плос­костью какого-либо другого тела, между которыми дей­ствует сухое трение; чтобы изобразить поведение пла­стического тела, груз надо соединить с гуковой пружи­ной и перемещать его по плоскостям скольжения.

При построении моделей тел со сложными реологи­ческими свойствами простейшие модели (элементы) сое­
диняют либо парал­лельно (Ь), либо по­следовательно (—). В случае параллель­ного соединения эле­ментов напряжения, действующие в них, суммируются, тогда как скорости удлине­ния каждого элемента сохр ан яются один а ко - выми. При последова­тельном соединении элементов скорости-уд­линения их суммиру­ют, при этом каждый элемент испытывает одно и то же напряже­ние. Эти два принципа являются определяю­щими при составлений реологических уравне­ний. Модели могут быть выражены струк­турными формулами, например Н—N или H|N.

Исследованиями [4, 5, 86, 116] показано, что реоло­гические параметры цементного геля при сдвиге могут быть экспериментально определены с привлечением уравнений Бингама и Букингама, а кинетика деформи­рования с учетом временных эффектов описана соот­ветствующим сочетанием элементов Кельвина и Макс­велла.

Поведение пластично-вязкого тела изображается мо­делью (рис. 2.1), отвечающей следующей структурной формуле: B = N — StV. (2.1)

Эта формула и модель соответствуют телу Бингама, которое способно сопротивляться пластическому тече­нию как посредством статического трения (тело Сен-Ве - наца), так и вязкостью (тело Ньютона), или пластиче­ской вязкостью — 1пл-

Кроме указанных трёх видов деформаций тел (упру­гость, вязкость и пластичность) важным свойством яв - 72
Ляется запаздывание упругих деформаций (эластич­ность). Механической модели, воспроизводящей свойст­ва жёстковязкого (эластичного) тела Кельвина (иногда его называют телом Фойгта), отвечает структурная фор­мула

К — H/N. (2.2)

Из модели (рис. 2.2,а), соответствующей этому урав­нению, следует, что при разгрузке пружина должна воз­вращаться в исходное положение и её вязкое сопротив­ление идентично вязкому сопротивлению твёрдого те­ла — которое оказывает тормозящее действие как при проявлении, так и исчезновении упругих деформаций. Суммируя напряжения, цолучим известное реологическое уравнение тела Кельвина. При больших значениях ^ап. деформация тела Кельвина будет развиваться непрерыв­но, но с убывающей скоростью. Такое медленное тече­ние по своему характеру аналогично явлению ползуче­сти, наблюдаемому в реальных твёрдых телах под влия­нием постоянно действующей нагрузки. В предельном случае при T=Oo величина сдвига составит T/GK (где GK— Модуль сдвига), в связи с чем упругий сдвиг произойдет не мгновенно а с запаздыванием (под влиянием упру­гого «преддействия»), характеризуемым временем (пе­риодом) запаздывания /зап..

Если в момент T=T разгрузить тело, т. е. т=0, тог­да вследствие упругого последействия или эластичности тела деформация сдвига медленно спадет и может вовсе исчезнуть теоретически при T—Oo (рис. 2.3).

Если соедините элементы Н и N последовательно, т. е. суммировать не напряжения при одной общей де­формации, а скорости относительных деформаций, то образуется реологическая, модель Максвелла со струк­турной формулой М=Н—N, характеризующая упруго - вязкое тело. Последнее представляет собой вещество (жидкость), так как под влиянием постоянно действую­щей нагрузки оно течет. Упругость сдвигл такого веще­ства, присущая большинству коллоидных (структуриро­ванных) систем, в отличие от твердых тел, не постоянна во времени и подвержена релаксационным процессам. Релаксация проявляется в виде затухания или ослабле­ния напряжений с течением времени при постоянной (не­изменной) деформации тела. Если время релаксации велико, то тело релаксирует медленно, когда же время
релаксации мало, то ослабление системы происходит быстро. Система, обладающая релаксационной текуче­стью, обусловленной способностью медленно течь при действии на нее постоянной нагрузки, превышающей предел текучести, обычно не обнаруживает упругого по­следействия, которое, как это было показано, свойствен­но кельвиному твердому упруговязкому (или жестковяз - кому) телу.

Из опытов с цементным гелем нормальной густоты следует [4, 116], что при мгновенном напряжении т меньше предела упругости туп цементный гель ведет себя как нерелаксирующее тело, претерпевающее, одна­ко, упругие деформации. При быстром приложении на­грузки полная деформация системы сразу не достига­ется. Деформация длится несколько минут. После снятия нагрузки она постепенно исчезает. При этом диаграмма

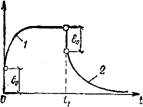
«т—е» показывает наличие мгновенной упругой дефор­мации ео как при нагруже - нии, так и при снятии деа - грузки. При напряжениях, превышающих предел теку­чести тт, намечаются участ­ки (рис. 2.4), характеризую­щие запаздывание деформа­ций. В момент приложения нагрузки возникает мгно­венная упругая деформация нейный участок упругопла - стических (эластических) деформаций, переходящий 8q, затем следует криволи-

В прямолинейный участок чисто пластических деформа­ций. В момент снятия нагрузки деформация мгновенно уменьшается на величину, равную мгновенной упругой деформации ej, и в последующем происходит постепен­ный спад деформаций в результате упругого последей­ствия. Затем исчезает запаздывающая деформация, и система переходит в состояние текучести.

В общем случае цементный гель является упруго-пла­стично-вязким телом, однако при В/Ц=Ки. т он претер­певает только упругие деформации до напряжения сдви­га 124—132 Па, в то время как при напряжениях 148— 150 Па появляются деформации, характеризующие ре­лаксационную текучесть системы. Следовательно, при достаточно мадых напряжениях сдвига т<тт кйнетика развития деформации ограничивается одним упругим последействием, при" этом вся возникшая деформация обратима.

При т^тт кривые показывают непрерывное нараста­ние остаточной деформации с переходом к стационарно­му течению после того, как упругое последействие в по­токе завершено. Вдоль такой кривой Dz/Dt стремится к наименьшему постоянному значению (De/Dt)0Ст. Разгруз­ка, фиксируемая в любой точке кривой после появления текучести системы, показывает, что остаточная деформа­ция нарастает с момента нагружения с той же постоян­ной скоростью, как и после разгрузки. В области малых напряжений сдвига т<тт наблюдается медленное тече­ние, характеризующееся текучестью с постоянной пре­дельно большой вязкостью, поскольку течение обуслов­ливается периодическим восстановлением нарушенной коагуляционной структуры.

С дальнейшим повышением напряжения сдвига по­степенно разрушается связность системы и в момент, когда T^Sto (где то — предельное напряжение сдвига)/ наблюдается скачок, при котором наступает лавинное разрушение структуры.

Как следует из рис. 2.4, а также результатов исследо­ваний [42, 107, 119], упруго-пластично-вязкие сйстемы обладают свойствами', присущими элементам Кельвина и Максвелла.

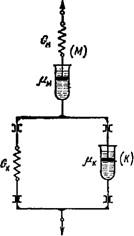
Реологическая модель, учитывающая упруговязкие и эластические свойства цементного геля, может быть по­лучена при последовательном соединении комплексов К и М (рис. 2.5). В этом случае наличие вязкого элемента

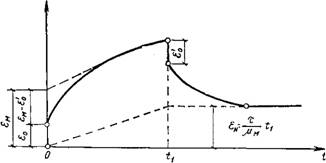
Позволит моделировать непрерывное увеличение дефор­мации во времени, т. е. имитировать незатухающее те­чение (ползучесть) цементного геля под влиянием постоянной нагрузки. Модель такого типа предложена Бюргерсом, а затем исследована в работе [102, 108] для условий, когда действует постоянное напряжение сдвига, наиболее распространенное на практике. Деформация тела Бюргерса определяется суммой деформаций комп­лексов К и М. Под влиянием постоянного напряжения в теле Бюргерса возникают два типа деформаций: в нача­ле— запаздывающая упругая де­формация, которая постпенно за­тухает и теоретически исчезает через бесконечно большой проме­жуток времени. Эта эластическая деформация восстанавливается после снятия нагрузки и, зату­хая при постоянно действующем напряжении, переходит в вязкое течение с постоянной скоростью (рис. 2.6).

Полная аналогия механизма деформирования, изображенно­го на рис. 2.6 с эксперименталь­ной кривой (см. рис. 2.4), свиде­тельствует о том, что реологичес­кая модель тела Бюргерса, близ­кая по своим свойствам к моде - Рис. 2.5. Реологическая ли Кельвина — Максвелла, до - Модель Бюргерса статочно хорошо описывает по-

Е

Ведение цементного геля при оговоренных ранее консистенциях. С увеличением количества воды в це­ментном геле все большее значение приобретает комп­лекс М, т. е. вязкий элемент модели, поскольку водона - сыщенная система утрачивает в той или иной мере упругие свойства, присущие комплексу К: С другой сто­роны, на сильно концентрированный цементный гель вязкая составляющая модели оказывает исчезающе ма­лое влияние и преобладает комплекс /С.