РЕОЛОГИЧЕСКИЕ ПАРАМЕТРЫ ЦЕМЕНТНОГО ГЕЛЯ
 2 января, 2013
2 января, 2013  admin
admin Из приведенного выше следует, что по абсолютным величинам (модулям сдвига, пределу прочности структуры) упругие свойства структурированных систем малы по сравнению с упругими свойствами твердых тел, поэтому ими обычно пренебрегают, рассматривают лишь структурную (пластическую) вязкость, которая является сравнительно очень высокой, более; заметной и легкоизмеримой.
В области малых напряжений сдвига пластическая вязкость, соответствующая телу Бингама, будет наибольшей и не зависящей от скорости сдвига. Это свидетельствует о медленном течении систем с нарушенной (но не разрушенной структурой), которая успевает восстанавливаться в, самом процессе течения.
Если возникающие (при течении) напряжения сдвига выше предела упругости для данной системы, то в таком случае коэффициент вязкости будет зависеть от степени нарушения структурной связности и может достигать наименьшего значения при полном ее разрушении, поэтому понятие о вязкости, как о величине постоянной, не может быть в общем случае распространено на структурированные системы. В широком диапазоне скоростей сдвига подвижность таких систем зависит от степени нарушения структуры, поэтому вязкие свойства правильнее характеризовать двумя параметрами; коэффициентом вязкости и соответствующим напряжением сдвига. Как известно, для многих неньютоновских жидкостей кривые течения могут быть описаны уравнением Бингама:
Система, течение которой следует этому уравнению, является идеально пластичным веществом. Под действием напряжений меньше предела пластичности оно вообще не течет, т. е. т—т0=0. Однако большинство так называемых вязкопластических систем обнаруживает отклонения от уравнения (2.3). Результаты многих исследований показывают, что цементный гель не является идеально-пластическим телом, поэтому уравнение (2.3) не может быть использовано в том виде, в каком его предложил Бингам.
Учитывая вязкопластические свойства цементного геля в диапазоне X от 1 до 1,65, в уравнение (2.3) Н. В. Шведовым введена вместо Рт величина предельного напряжения сдвига то, являющаяся более характерным параметром текучести при скоростях сдвига, возникающих при вибрации, перекачивании насосами и т. п. [5, 86]. В этом случае применительно к условиям течения цементного геля по цилиндрической трубе, уравнение (2.3) примет вид:
Dv 1
Dp Ц
Где т — напряжение сдвига, соответствующее данному градиенту скорости; и — общая вязкость системы, состоящая из двух слагаемых:
^ = (2.5)
Fxjv — нормальная или ньютоновская вязкость; [лСтр — структурная вязкость, вызванная добавочным сопротивлением движению со стороны разрушенных элементов структуры цементного геля
Для бесструктурных жидкостей то=0, |iCTP=0 и уравнение (2.4) будет соответствовать уравнению гидродинамики Ньютона, интегралом которого для случая истечения через цилиндрическую трубу (капилляр) является известное выражение Пуазейля:
Согласно уравнению Шведова — Бингама (2.4), течение цементного геля через цилиндрическую трубу представляется следующим образом. Движущаяся система рассматривается^ как состоящая из бесконечного числа коаксиальных полых цилиндров, перемещающихся относительно друг друга с различной скоростью, которая возрастает от стенки трубы к ее оси. При этом предполагается, что скорость слоя, прилегающего к стенке трубы, равна нулю, а скорость слоев, близких к оси трубы, наибольшая. В связи с этим в структурных связях, обусловив
ленных силами Ван-дер-Ваальса возникают напряжения сдвига, убывающие с увеличением скорости от стенки Трубы в направлении оси потока. Часть потока, ограниченная поверхностью радиуса г0, перестает течь и движется йодобно упругопластическому телу с одинаковой скоростью VR.
Вследствие отмеченных явлений распределение скоростей в цилиндрической трубе в направлении, перпендикулярном потоку, должно происходить по усеченной параболе (рис. 2.7).
Соответствующий профиль распределения скоростей при вязкопластическом течении системы формируется следующим образом: весь поток в трубе может рассматриваться как бы состоящим из двух частей: так называемого входного участка и области структурного течения. : Во входном участке материал^поступающий в трубу, испытывает тормозящее действие стенок. В связи с этим первоначальный "прямолинейный профиль скоростей постоянно преобразовывается и принимает вид усеченной параболы, пределом которого при вязком течении жидкости является пуазейлевский (параболический) профиль.
Длина входного участка, в пределах которого формируется профиль распределения скоростей по сечению потока, зависит, очевидно, от толщины пристенного слоя, с его увеличением диаметр внутреннего ядра потока будет уменьшаться. Уменьшение диаметра ядра сопровождается ускорением течения, поскольку общее количество протекающей массы должно оставаться постоянным. После
Прохождения потоком Рис- 2-7- Распределение скоростей Некоторого участка в поперечном сечении потока
Трубы формирование профиля распределения скоростей заканчивается, и течение происходит уже по установившейся закономерности.
|
|
В целях проверки применимости уравнения (2.4) к свойствам цементного геля были изучены режимы течения по цилиндрическим трубам диаметром от 0,016 до 0,1 м и длиной от 1 до 4 м при постоянном и переменном напоре.
Ом
|
Рис. 2.$. Характерные профили потока цементного геля в зависимости от значений X
Нии в цилиндрической трубе I . ■ , I T Рис. 2.10. Зависимость г/г0 от 1 1,2 Tf W Tf 1,6 X для цементного геля |
В опытах использовали несколько сортов цемента различного минералогического состава. Было установлено, что при характер движения цементного геля резко меняется (рис. 2.8). При водоцементных отношениях, соответствующих упругопластическому состоянию, система не деформируясь скользит по стенке цилиндрической трубы и ядром служит все сечение трубы г0=г. В этом случае при Х=1 в пристенном слое возникают напряжения (около 150 Па), что значительно меньше предельного напряжения сдвига (246—260 Па), поэтому в пристенном слое течение цементного геля обусловливается пластическими деформациями, т. е. релаксационной ползучестью. С увеличением водоцементного отношения, сопротивление цементного геля сдвигу становится меньше» чем напряжение сдвига, возникающее у стенок трубы. В связи с этим ядро занимает в потоке сравнительно меньшее место: г0=г/п.
|
Кнг 1,25 Кнг 1,52Кнг Кп^65Киг >Кп
|
Как уже указывалось, если напряжение сдвига т незначительно превосходит т0 (при небольших перепадах давления) и цементный гель течет как вязкопластичес- кая масса, тогда можно пренебречь инерционными силами по сравнению с большими силами трения. Приняв для этого случая, что то есть величина. постоянная, определим радиус ядра цементного геля. Если — площадь
Сечения ядра, то сила, сдвигающая его, будет равна (рис. 2.9):
Т = яг20Р, (2.7)
Где Р —разность давлений на концах трубы, приходящаяся на единицу площади ее сечения.
Сила трения, преодолеваемая ядром по длине потока - (длине трубы /), будет равна
Г = 2яг0/т0. (2.8)
При равновесии этих сил, т. е.
Jv§P — 2л;го/то = 0,
Находим, что
Г.-^. (2.9)
Будем исходить из того, что давление, необходимое для преодоления только начального сопротивления сдвига то, равно Роу тогда из рассмотрения равновесия сил на стенках трубы найдем
T0=-^-/V (2.10)
Аналогично для любого цилиндрическбго потока радиуса р>г0 имеем
R = Fp. (2.11)
Экспериментально установлено [4], что величина радиуса ядра потока при вязкопластическом течении цементного геля зависит не только от прочности структуры, но и от диаметра трубы. Однако отношение г/г0 для данного значения X является величиной постоянной (рис. 2.10).
Проинтегрируем уравнение (2.4) в пределах от г до го и подставим в него вместо т его значение (2.11). В результате получим закон распределения скоростей по сечению трубы:
Часть потока, ограниченная радиусой г0, не деформируется и движется внутри трубы как упругопластическое тело со скоростью
Г.). (2.13)
При отсутствии в потоке ядра, т. е. г0=0 и т0=0, вещество течет как обычная вязкая жидкость с осевой скоростью:
»оси=^. (2.14)
Сравнивая формулы (2.14) и (2.13), мы видим, что последняя отличается дополнительным параметром, учитывающим пластические свойства цементного геля.
Взаимосвязь между скоростью течения ядра вязко - пластической массы и вязкой жидкостью можно определить, пользуясь выражениями (2.13) и (2.14), а именно
Подставив* вместо то его значение (2.10), после преобразований получим
»0 = "оси [ (1 - 'о/'2) - V 0 - V0 ] • (2.:16)
Из уравнения следует, что скорость течения цементного геля по трубопроводу при вязкопластическом режиме всегда меньше скорости течения обычной вязкой жидкости. Только в частном случае, если т значительно превзойдет то, структурные связи в цементном геле окажутся разрушенными и тогда он будет течь со скоростью, рав-
ЙОЙ Роси.
Иначе, чем это было описано, происходит истечение цементного геля под действием собственной массы из вертикальной цилиндрической трубы при изменяющемся напоре: ядро значительно опережает пристенный слой, отрывается от него и медленно сползает из трубы; затем появляется полый цилиндр, непосредственно соприкасающийся со стенкой трубы. Такой характер истечения цементного геля из вертикальной трубы объясняется неравномерным распределением действующих сил (силы тяжести) во всем его объеме и неуравновешенностью нормальных сил в нижнем сечении.
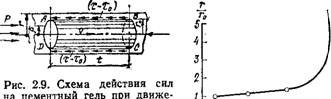
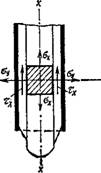
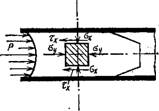
По мере увеличения деформации вместе с развитием касательных напряжений %х по коаксиальным поверхностям появляются осевые растягивающие напряжения gX и, как следствие этого, поперечные ^растягивающие напряжения Gy, которые нарушают структурные связи цементного геля и тем самым значительно снижают величину то (рис. 2.11).
|
Ю |
|
|
|
-у у |
|
Рис. 2.11. Действие сил при течении цементного геля в цилиндрической трубе |
|
У— |
<9
А — вертикальной сверху вниз; б—горизонтальной и вертикальной снизу вверх
Под влиянием всестороннего растяжения ядро отрывается от пристенного слоя и самостоятельно сползает из трубы до выхода остальной части. При движении цементного геля по горизонтальной трубе или же по вертикальной трубе снизу вверх в ядре возникает трехосное сжатие (рис. 2,41,6), поэтому сохраняется связанность ядра потока с пристенным слоем цементного геля. При значительных сопротивлениях течению всестороннее сжатие может привести к закупорке трубы, вследствие потери цементным гелем (при отслоении из него жидкости) требуемой текучести.
|
—Fdz |
|
Рис. 2.12. давления |
|
Распределение в конической |
|
Трубе (насадке) |
|
6* |
|
83 |
Исследования реологических свойств коллоидных систем впервые были начаты Н. Ф. Шведовым, который пользовался прибором с коаксиальными цилиндрами. Приборы такого типа широко применяются при изучении коллоидных систем и сейчас. Не останавливаясь подробно на всех методах измерения, отметим, что эти приборы позволяют измерять вязкость слабоконцентриро
ванных структурированных систем в достаточно широких интервалах скоростей сдвига. Однако для цементного геля, являющегося сильно концентрированной системой, целесообразнее метод, основанный на измерении объемной скорости (расхода) течения через трубу, при различных перепадах давления (скоростях сдвига). Этот метод удобен тем, что он позволяет связать взаимно режимы течения, цементного геля с параметрами его вязкости при различных перепадах давления и водоцементных отношениях, что весьма важно при решении ряда производственных задач, связанных с вибрированием бетонных смесей, транспортированием при помощи насосов и т. п. Для глинистых растворов указанный метод исследований был использован в работе [136], а для цементного геля применен в [86] [4].
Для исследования реологических свойств цементного геля пригоден вискозиметр, отличающийся от обычных, используемых для измерения вязкости нормальных жидкостей, конической формой и диаметром трубки. Это обусловлено необходимостью воспрепятствования отрыву ядра от пристенной части потока, а также проскальзыванию упругопластических систем, наблюдающемуся при движении по цилиндрической трубе.
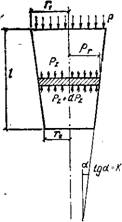
Пользуясь уравнением (2.4), выведем необходимые расчетные формулы для определения коэффициента вязкости и величины предельного напряжения сдвига цементного геля. Для этого рассмотрим задачу о продав - ливании упругопластической массы через коническую трубу (рис. 2.12). Выделим горизонтальными параллельными сечениями элементарный объем конической трубы, заполненный цементным гелем, и предположим, что давление распределено по сечению равномерно, считая, что падение давления Pz по длине трубы есть некоторая функция от 2.
Радиус ядра цементного геля определится так: если пг — площадь сечения ядра потока, то сила, сдвигающая ядро, будет равна
Nrgd/V (2.17)
Сила сопротивления, обусловленная структурной связанностью "цементного геля на элементарном участке Dz Трубы, составляет
2яг0т^г. (2.18)
Из условия равновесия этих сил получим, что
(2.19)
Следовательно, в данном случае г0 есть величина переменная, так как падение давления, приходящееся на единицу длины трубы в ее узком конце, больше, чем в широком. Аналогично для любого конического слоя радиуса р>г0 имеем
2Xdz
Р = —• (2.20)
Для получения закона распределения скоростей по коническому сечению воспользуемся выражениями (2.4) и (2.20):
1 dPzp Ц [ 2dz
После соответствующих преобразований получим
Где г — переменный радиус конуса; р — радиус коаксиального слоя в рассматриваемом сечении трубы р^г0.
|
Dv = ~ l-^rdf1" — то (2.21) |
Скорость ядра потока может быть определена из условия, что р равняется го
|
DP2 г* , dz |
|
__ |
|
4Dz dP2 |
Т0R . (2.23)
Расход цементного геля через коническую трубу может быть представлен в следующем виде:
Г0 г
Q = J 2npv0dp + J* 2npvdp. (2.24)
Внося в (2.24) значения для V и V0 из (2.22) и (2.23), после «интегрирования получим
„=DP ^ 4/3 jwi+_l_ /2 s*y i
4 8ndz [ г ' г т 3 (dPzf г ) .
|
(2.25) |
Уравнение (2.25) трудноразрешимо относительно DPz если же пренебречь последним членом как величи
ной малой высшего порядка, можно получить упрощенную формулу следующего вида:
[dPe-4/3^L]. (2.26)
8[Idz
Решив уравнение (2.26) относительно DPz и принимая r=ri+Јz, где K = Tga= (рис. 2.12),^имеем
+ (2-27)
Я (Г1 — кг) 3 rxkz
Отсюда после интегрирования в пределах от 0 до / получим окончательно
J-U^-to-a.. (2.28)
П 3k [4 r) '2
Заменив давление напором, можно написать
U _ / _L—_L —In — , (2.29)
36 ^ гз гз J 3kgyr r%
Где Н — высота напора, см; гх и г2 — соответственно, радиус большего и меньшего отверстия трубы, см; q — расход, см3/с; у г — объемная масса геля, г/см3.
При вязкопластическом течении системы общая потеря напора слагается из сумм потерь на преодоление сопротивления структурной связности и на живую силу вытекающей струи, т. е.
Я = ЯХ + Я2. (2.30)
Для вычисления первого члена можно воспользоваться уравнением (2.29), подставив в него соответствующие размеры трубки:
Г = 0,5см; — 0,4; 6 = 0,01;
#1==0,66 — <7 + 0,061 — . (2.31)
YD YP
Потеря напора на живую силу сравнительно невелика и мало отражается на точности расчетов. Для определения этой части потери напора может быть использована формула, выведенная на основании теории переменной вязкости.
Минуя промежуточные выкладки, связанные с выводом формулы для #2, приводим окончательное ее выражение:
Н% = Bq2, (2.32)
Где В — коэффициент, варьирующий в пределах от 0,00216 до 0,00248. Не допуская существенной погрешности можно принять среднее его значение 0,00232.
В таком случае для определения вязких свойств цементного геля при истечении под постоянным напором получим следующую расчетную формулу:
Н = 0,66FJt/7P Q + 0,06LT0/Vr + 0,00232<72. (2.33)
Уравнение (2.33) содержит две неизвестные величины —- i и to, в связи с чем необходимо не менее двух наблюдений при разных по величине, но постоянных в каждом случае напорах. Для описания истечения вязкопла - стических систем под влиянием переменного напора формула (2.33) не может быть применена, поскольку при ее выводе предполагалось, что Н=const.
Для этого случая уравнение (2.33) необходимо пред-
Ставить в таком виде, исходя из допущения, что Q=F—,
Dt
Где F— площадь основания цилиндра вискозиметра:
Н = 0,66— F + 0,061 ^- + BMF (Ур? . (2.34) Yr Dt Yr Dt J
Решим дифференциальное уравнение (2.34) относи - Dff '
Тельно ----- , приняв £=0,0025-и F=200 мм2, и, разде-
Dt
Лив переменные, получим Dt = DH * (2.35)
0,66 — — Л/ 0,43б(—У — 0,00061 —+ 0,01Я Yr У Yr / Yr
Интегрируя (2.35) (правую часть в пределах от T0 до T и левую часть в пределах от H0 до H), получим
|
• 132— In Yr |
|
0,66 — Yr |
— j/" 0,436 ^j2 —0,00061 у- +0,01 H —
|
H=ht H=h2 |
|
(2.36) |
- 2000,436 ^ J -0,00061 ^ + 0,01Я где T — время истечения от уровня H0 до HXt
Введем следующие обозначения:
|
Г — 0,00061 — + 0,01Л0 ; Yr — 0,00061 — + 0,01%. |
|
(2.37) (2.38) |
|
Yr |
C.= J/" 0,43б(-Ь)а Cl- 0,436 (J-J-
Окончательно имеем:
0,66-^ -С0
Т= 132 -^Ln1------------- -------------- Ь200 (С0 —Cx). (2.39)
Yr 0,66-^ - Ci Yr
Уравнение (2.39) описывает движение вязкопласти - ческой системы через коническую трубу при переменном напоре. В этом случае для определения параметров вязкости fi и to необходимо иметь два измерения: одно при переменном напоре, а другое при постоянном, и затем решить совместно уравнения (2.33) и (2.39).
Для упрощения подсчета может быть рекомендован следующий прием: сначала применяют формулу (2.33) для обоих случаев истечения (в том числе при переменном напоре). При этом исходят из того, что Н — постоянная величина, равная. Потом вычисленные величины х/уг и to/vr подставляют в формулу (2.39) и если при этом получается время Т, отличающееся от измеренного в действительности, то несколько уменьшают среднее значение Н и этот же прием повторяют вновь пока не будет получена удовлетворительная сходимость.
Прибор для измерения вязких свойств цементного геля представляет собой несколько видоизмененный вискозиметр Энглера с приспособлениями, позволяющими варьировать величину давления, под которым выдавливается цементный гель через коническую трубу [5].
Параметры вязкости цементного геля при Х>1,65 измеряют при поддержании постоянного давления в приборе в течение опыта. Менее подвижные смеси выдавливались из трубки как под постоянным давлением, так и при различных перепадах давления, создававших напряжения, близкие по величине к предельному напряжению сдвига цементного геля.
Напряжение сдвига и коэффициент вязкости цементного геля при различных значениях X от 1 до 1,65 опре
деляют по данным двух опытов при различных расходах q, обусловленных близкими по величине напорами (давлениями) .
При Х< 1 цементный гель представляет собой земли - стовлажную массу, состоящую в основном из несвязанных между собой цементных комков (микроагрегатов) различных размеров. Для их слияния в сплошное тело необходимо воздействовать на микроагрегаты вибрацией при частоте колебаний не менее 100 Гц.
В уплотненном состоянии такой цементный гель подобен квазитвердому телу с явно выраженными упругопла - стическими свойствами; для определения его реологических параметров вискозиметрический метод оказывается непригодным. В этом случае предельное напряжение сдвига то можно измерить испытанием в сдвиговом приборе [5].
Величина сдвигающего груза зависит не только от структурной прочности цементного геля, но и от нормального давления, обусловленного его собственной массой. Если по оси ординат откладывать сдвигающее напряжение т, а по оси абсцисс нормальное напряжение, равное Yr/i (где H — высота слоя цементного геля), то каждому значению X будет соответствовать кривая, отсекающая на оси абсцисс различные по величине отрезки С Для удобства использования графической зависимости криволинейное очертание заменяют близкой к ней прямой (рис. 2.13)/В таком случае общее сдвигающее напряжение можно записать в виде
■ т = С + т',
Где Y=Hyr tg а, т. е. т'=а tg а. Следовательно,
Т = C + atga. (2.40)
Выражение (2.40) соответствует зависимости Кулона для связных грунтов, при этом параметр С может быть интерпретирован как коэффициент сцепления грунта при сдвиге, а tga=/ — как коэффициент внутреннего (статического) трения. Для сыпучих грунтов С=0 и тогда
* = crtga. (2.41)
В обычных жидкостях С=0 и т не зависит от нормального напряжения; в этом случае напряжение сдвига может быть выражено в функции от вязкого сопротивления жидкости.
Надо заметить, что в ряде работ по механике грунтов, например в [125], не рекомендуется придавать параметрам, входящим в уравнение (2.40), непосредственный физический смысл в виде коэффициентов трения и величины сцепления, полагая, что непосредственный физический смысл имеет только полная величина сопротивления сдвигу т.
Такая точка зрения может быть оправдана при рассмотрении несущей способности грунтов, служащих основанием для сооружений, так как в этом случае практический интерес имеет поведение всего подстилающего слоя, свойства которого изменяются в широких пределах в зависимости от множества факторов: влажности, переуплотнения грунта и т. п.
В рассматриваемом же случае, когда с достаточной степенью точности можно регулировать консистенцию и плотность цементного геля, создавать требуемые условия для воспроизведения напряженного состояния при сдвиге и т. д., придавать непосредственный физический смысл упомянутым параметрам вполне оправдано.
Коль скоро связность цементного геля появляется только при определенных добавках воды и этим обусловливается его сопротивление сдвигу* то это дает нам право считать параметр С величиной предельного напряжения сдвига to.
Величина то, определенная из условия предельного, равновесия системы (при весьма малых скоростях деформации), характеризует сопротивление цементного геля в момент срыва, т. е. то минимальное напряжение сдвига, при котором нарушаются (разрываются) структурные связи в цементном геле.
|
Рис. 2.13. Зависимость напряжения сдвига от нормального давления |
Сопротивление структуры цементного геля сдвигу и растяжению обусловливается в основном ван-дер-вааль - совым притяжением, так как силы электростатического и магнйтного притяжения, а также валентные силы более короткодействующие, чем сила отталкивания. Кроме этого, указанные силы зависят в значительной мере от
полярности взаимодействующих частиц и при оводнении быстро нейтрализуются.
Если обозначить через ег—коэффициент пористости цементного геля; —диаметр частиц; ац — расстояние между активными центрами на их поверхности, тогда сила ван-дертваальсового притяжения между двумя минеральными частицами может быть выражена уравнением:
Дв = 0,047 —-4г Т- > (2А2)
4 **
Где коэффициент А оценивается порядком
Из уравнения (2.42) видно, что сила ван-дер-ваальсового притяжения возрастает с уменьшением/пористости и расстояния между твердыми частицами. Эта взаимосвязь между сопротивлением сдвига структуры цементного геля и плотностью упаковки цементных частиц четко прослеживается по экспериментальным данным.
Интегральная кривая изменения величины предельного напряжения сдвига цементного геля в зависимости от значений X, полученная методом ^ вискозиметрии и на сдвигаемом приборе, приведена на рис. 2.14.
В экспериментах были использованы цементы различных видов, в том числе глиноземистый. На том же рисунке показана интегральная кривая изменения вязкости р, г (рис. 2.14,6), измеренная при истечении цементного геля в диапазоне значений X от 1 до 1,65 (Х<1, цементный гель не способен течь или выдав-
Рис. 2.14. Изменение т0(а) и вязкости Jir, (б) цементного геля в зависимости от X
Ливаться из конической трубки вискозиметра, так как в этом случае происходит уплотнение — запрессовывание системы).
Кривая рис. 2.14 показывает, что процесс упрочнения структуры цементного геля происходит до значения Х = =0,876, при котором to достигает максимальной величины 1040 Па (10,6 г/см2), а затем с повышением содержания воды то уменьшается и при Х=1,65 оно практически соизмеримо с вязкостью цементного геля. Объясняется это ослаблением сил связи между частицами твердой фазы, обусловленным образованием более толстых сольватных» оболочек и возникновением расклинивающего давления воды в, плоскости сдвига под влиянием напряженного состояния (эффекта П. А. Ребиндера). -
Экспериментальные данные других исследователей, например авторов работы [50], удовлетворительно совпадают с приведенными значениями то. Здесь важно заметить, что, несмотря ga некоторое различие в минералогическом составе и дисперсности цементов, при соответствующих значениях X практически формируются идентичные по прочности внутренних связей структуры цементного геля. Это обстоятельство позволяет использовать лишь один раз построенную интегральную кривую то=ф(Х) для решения различных технологических задач, связанных с учетом реологических свойств цементного геля.
При вибрационном воздействии на цементный гель значение т0 значительно уменьшается и может равняться нулю при полном разрушении сил ван-дер-ввальсового взаимодействия. Это свидетельствует о том, что то — в
ТАБЛИЦА 2.1. ВЛИЯНИЕ ВИБРАЦИИ (©„-50 Гц, а-0,175 см) НА
|
ИЗМЕНЕНИЕ т0 И Fr
|
Общем случае величина непостоянная для цементного геля данной консистенции, а именно т0 может возрасти под влиянием уплотняющего нормального давления (напряжения) или снизиться до нуля в зависимости от скорости деформации структуры цементного геля (табл. 2.1).
Из табл. 2.1 следует, что при Х=0,876 и 1 структурные связи в цементном геле разрушаются не полностью. Под влиянием вибрации с частотой 50 Гц цементный гель при Х=0,876 обладает более прочной структурной связностью, чем при Х=1. Следовательно, при частоте колебаний 50 Гц не может быть достигнута надлежащая скорость деформации структуры цементного геля, когда полностью могли бы быть разрушены силы внутреннего взаимодействия между зернами твердой фазы. В несколько меньшей мере сказанное относится и к цементному гелю при Х=. В этом случае то уменьшается примерно в 22 раза. Вмёсте с тем при большем водосодержа - йии кратковременная вибрация (до 6 с) вполне достаточна для практически полного разрушения структурных связей цементного геля.
Если скорость деформации сдвига сравнительно невелика, что бывает в отдельных^случаях при вибрационном воздействии, а также в процессе перекачивания смесей насосами по трубам, то полного разрушения структурных связей цементного геля не произойдет, поэтому следует различать напряжение сдвига то, определяющее сопротивление цементного геля срыву (например, в момент пуска насоса), и остаточное напряжение сдвига т0СТ — После нарушения структурной связности при данной скорости деформации сдвига (стабилизированное состояние).
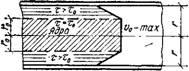
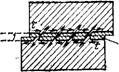
Остаточное или стабилизированное напряжение сдвига обусловливается неполной десольватациёй частиц твердой фазы, т. е. наличием в цементном геле очагов связанных структур, оказывающих сопротивление сдвигу. Такие очаги, обнаруженные после сдвига, состоят из вытянутых слоев цементного геля, ориентированных к плоскости сдвига под углом примерна 45°. Они выступают из тонкой водной пленки, образовавшейся в результате частичной десольватации зерен цемента в зоне сдвига (рис. 2.15). Отсюда следует, что разрушение структурных связей цементного геля при сдвиге происходит от разрыва их под влиянием главных растягивающих напряжений. Можно предположить, что структур
ные связи, сохранившиеся в цементном геле при вибрационном воздействии, не утрачивают своих упруго - пластических качеств и способны сопротивляться действию главных растягивающих напряжений, возникающих при деформациях сдвига.
Как и т0, коэффициент внутреннего трения можно рассматривать в качестве составной характеристики реологических свойств цементного геля, поскольку каждому значению X соответствует определенная величина fr. В случае полного (объемного) разрушения структуры коэффициент fr цементного геля независимо от его водо - содержания приобретает постоянное значение, равное примерно 0,012, и соответствует коэффициенту вязкости «воды», - поэтому при течении цементного геля с полностью разрушенными структурными связями основным реологическим критерием может служить коэффициент вязкости. Значительное снижение значений Fr под влиянием вибрационных импульсов является следствием насыщения зоьг сдвига избыточным количеством жидкости в результате кратковременного перевода слабосвязанных диффузных слоев в состояние «свободной» жидкости. Рассматривая вязкие свойства цементного геля во взаимосвязи с его структурной прочностью, можно предположить, что коэффициент вязкости |яг утрачивает свою структурную составляющую — р, СТр (в условиях проведенных опытов) уже при Х=1,65, так как с увеличением скорости истечения вычисленные значения [хт для цементного геля при X^lfiS весьма незначительно отличаются друг от друга. Судя по результатам опытов, |Lir=[Xjv, т. е. р, г(вязкость воды при T—288 К равна 0,011)'; это может быть объяснено тем, что «турбулентность» в цементном геле наступает при значительно меньших числах Рейнольдса, чем в случае истечения бесструктурных жидкостей, для которых Re=2000.
|
|
|
^ . 1 — зона сдвига; 2 — водная пленка |
|
> Рис. 2.15. Очаги сопротивления сдвигу в цементном геле нормальной густоты |
При содержании в потоке твердых частиц и обломков разрушенной структуры критическое значение числа Рейнольдса может, согласно данным [107, 136], понижаться в 10 раз и более. Такая ранняя «турбулентность»
Обусловливается возникновением местных завихрений вокруг частиц твердой фазы, в связи с чем переход ламинарного режима в «турбулентный» сопровождается некоторым увеличением вязкости.
Зависимость коэффициента вязкости цементного геля от скорости истечения наблюдается только при водоце - ментных отношениях в пределах X от 1 до 1,65. Чем прочнее структура, тем значительнее падение р, г с увеличением давления, под которым цементный гель выдавливается из вискозиметра.
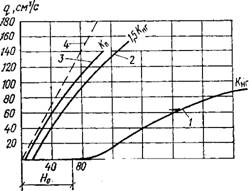
Зависимость вязких свойств цементного геля от величины напора может быть наглядно выражена функцией Q—F (Я) (где Q — расход через трубку; Я — напор). Результаты опытов (рис. 2.16) показывают, *1то для цементного геля кривые Q=F{H) не проходят через начало координат и отсекают на оси абсцисс некоторые отрезки, равные Я0. Только при этих минимальных напорах цементный гель начинает приобретать свойство текучести. При Х=1,65 кривая Q=F(H) пересекает ось абсцисс вблизи начала координат, и такая система по своим реологическим свойствам приближается к бесструктурным жидкостям (прямая OA). Эти опыты подтверждают, что при Л^1,65 система практически не обладает структурными связями.
Структурная связность цементного геля, характеризуемая Х=, нарушается при #о=0,75 м, что в перерасчете на то эквивалентно 264 Па. Затем следует криволинейный участок, в пределах которого продолжается разрушение структуры, заканчивающееся при Я=2,4— —2,6 м. Истечение цементного геля с разрушенной структурой происходит при постоянной вязкости (прямолинейный участок) так же, как и при нормальных жидкостях. Напор (давление), при котором цементный гель вовсе утрачивает свою связность, зависит от первоначальной плотности коагуляционной структуры, т. е. от X, а следовательно, от способа приготовления цементного геля и условий проведения опытов.
Реологические параметры цементного геля изменяются также при неоднократном повторном пропускании его через вискозиметр и в процессе перекачивания по трубам. Например, если перекачивать цементный гель по резиновому шлангу, организовав замкнутый цикл (раст - воронасос-бункер), то в этом случае по манометру можно заметить, что при повторных циркуляция* цементного
|
|
|
120 160 200 ZkQ 2QQHjCM |
|
Рис. 2.16. Реологические кривые: 1, * 2, 3 — цементного геля; 4—бесструктурной жидкости |
Геля давление снижается, т. е. сопротивление течению уменьшается. В процессе непрерывного нарушения структурных связей существенно отдаляется время, соответствующее началу схватывания цементного геля. Однако вместе с этим наступает момент, когда цементный гель мгновенно превращается в твердое тело с выделением значительного количества тепла, порядка 353— 263 К. Это необратимое явление, связанное с мгновенным превращением вязкопластической массы в твердое тело, минуя продолжительную промежуточную стадию завершения процесса коагуляционного структурообразо - вания цементного геля, свидетельствует об ускорении ионного обмена при продолжительной циркуляции (течении) цементного геля в замкнутом пространстве под влиянием сдвиговых напряжений, возникающих в потоке при перекачивании насосом. Аналогичный эффект можно наблюдать при продолжительной вибрации цементного геля и прочих интенсивных механических воздействиях.
Практически стабильные значения параметров вязкости цементного геля сохраняются в течение определенного времени и зависят от скорости физико-химических и фазовых превращений, возникающих при взаимодействии цементных частиц с водой. Образующийся вследствие этрго ионный раствор претерпевает количественные и качественные изменения, способствующие возникновению кристаллогидратных структур и упрочнению в них внутренних связей. Чем выше начальная концентрация твердой фазы в цементном геле—меньше X, тем быстрее утрачивается стабильность реологических параметров.
В качестве примера можно привести результаты опытов по определению изменения коэффициента вязкости шлакопорт - ландцементного геля при Х~ 1,65, или В/Ц=0,5 [63]. Исследования проводились на ротационном вискозиметре РВ-8, конструкция которого позволяла замерять вязкости через каждые 15 мин непосредственно в пуазах.
По рис. 2.17 можно заключить, что в течение 120 мин значения коэффициента вязкости цементного геля практически не изменяются, а затем они резко возрастают, достигая максимума при Г=300 мин, которое соответствует времени, определяющему конец схватывания цементного
Геля при Х~1,65 (при нормальной его густоте начало схватывания наступает через 140 мин по Вика).
При динамических (сдвиговых) воздействиях спонтанный процесс становления коагуляционной структуры нарушается, и несколько отодвигается момент, когда в цементном геле создаются условия для образования относительно более прочных связей между частицами твердой фазы.



 Опубликовано в
Опубликовано в