ОБЪЕМНЫЕ ДЕФОРМАЦИИ БЕТОННОЙ СМЕСИ ПРИ ВИБРАЦИОННОМ ВОЗДЕЙСТВИИ
 13 декабря, 2012
13 декабря, 2012  admin
admin Изменения объема бетонной смеси под действием вибрации зависят от плотности упаковки зерен заполнителя и частиц цемента. Перегруппировка твердой фазы происходит как в процессе формования изделий под влиянием амплитудных деформаций, т. е. колебательных движений зерен заполнителя, при которых они стремятся занять более устойчивое (компактное) расположение, так и в результате объемных деформаций цементного геля, способствующих сближению частиц цемента и вместе с этим — зерен заполнителя.
В цементном геле энергия колебательных движений поглощается при преодолении сопротивления сдзига то, сил тангенциальной вязкости и установлении нового энергетического состояния в структуре материала. Определенной плотности структуры цементного геля соответствует свое наиболее выгодное в энергетическом отношении взаимное расположение цементных частиц, а
|
А) |
|
|
|
Нос |
|
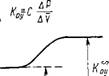
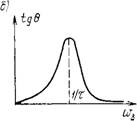
Рис. 8Л. Зависимость модуля объемной упругости (а) и тангенса угла сдвига фаз (б) от частоты колебаний |
Поэтому изменение его объема должно сопровождаться перегруппировкой частиц и определяться равновесным распределением энергии между колебательными, вращательными и поступательными движениями частиц твердой фазы. Кроме этого, деформация, при которой возникает течение материала, связана с непрерывной затратой энергии, превращающейся в тепло. Объемные деформации нарушают термодинамическое равновесие как в твердых телах, так и в жидкостях и вследствие этого всегда сопровождаются процессом восстановления равновесия, Модуль объемной упругости бетонной смеси (цементного геля) должен, в отличие от обычных жидкостей, зависеть от скорости деформации. Мож
но предположить, что модуль объемной упругости цементного геля изменяется от максимального «динамического» значения, соответствующего очень быстрым деформациям, при которых процесс становления равновесия не успевает следовать за изменением объема, до минимального «статического» значения, которое наблюдается при очень медленных деформациях, когда процесс становления равновесия полностью следует за изменением объема.
Известно, что при гармоническом режиме деформации объемная упругость некоторых жидкостей (это больше относится к структурированным гелям) характеризуется двумя величинами: отношением амплитуды давления к амплитуде деформации и углом сдвига фаз 0ф деформации и давления (напряжения). С увеличением частоты колебаний амплитуда деформации монотонно возрастает, а тангенс угла сдвига фаз tg 0ф при частоте (ов =l/tР (где /р — время релаксации) проходит через максимум (рис. 8.1). При очень малых и больших частотах колебаний tg Эф стремится к нулю, а модуль объемной упругости Ко. у стремится соответственно к своему статическому значению Кос и динамическому К™у. Следовательно, в области низких частот до озв =1/£р происходят обратимые деформации (нет потерь тепла) и течение отсутствует, т. е. цементный гель будет вести себя подобно упругому телу.
По мере увеличения частоты ((oB>l/fp) приложенного напряжения процессы нарушения и восстановления равновесия не будут успевать следовать за изменениями напряжения, и цементный гель начнет течь. Очевидно, что процессы течения в бетонной смеси могут проявляться при определенных режимах вибрирования, зависящих в каждом конкретном случае от структурной плотности цементного геля, т. е. от значений X.
Изменения объема при течении и внутренней перегруппировке частиц связаны с физико-химическими процессами и обусловливаются образованием более плотных коагуляционных структур цементного геля. На этом основании общая потеря энергии при вибрации цементного геля может быть выражена суммой
Лэ — Лтеч + Лпер» Где т|теч — поглощение энергии при разрушении структуры цементного геля в процессе течения; т|пер — поглощение энергии в процессе перегруппировки частиц.
21* 323
При формовании бетонной смеси т^ер составляет весьма незначительную часть от общей потери энергии и поэтому т]э=г1теч> т. е. энергия расходуется в основном на преодоление структурной связности цементного геля.
При высокочастотном вибрационном воздействии т)пер составляет большую часть общей потери энергии, так как после разжижения цементного геля энергия полностью расходуется на перегруппировку частиц цемента. Потери энергии при разрушении структуры цементного геля и перегруппировке частиц цемента зависят от расстояния между ними.
В процессе формования коэффициент затухания в бетонной смеси уменьшается и после определенной продолжительности воздействия он стабилизируется, достигая минимального значения. Этот момент соответствует окончанию формования, так как при большей продолжительности вибрирования изменения объема заполнителя не происходит. Изменения амплитуды колебаний в бетонной смеси обусловливаются поглощением энергии вибрации. Согласно [56], амплитуда колебаний ах звуковой волны в жидкостях на расстоянии /?р от источника возбуждения изменяется по следующеему экспоненциальному закону:
_ ®в. 0
— R Р------ sin —
А =апе св 2 .
|
Ав е |
Учитывая, что при малых углах сдвига фаз sin 0ф/2^=; ^ l/2tg 9ф, будем иметь
СОп
Скорость распространения звуковой волны Св в бетонной смеси пропорциональна скорости вибрирования, т. е. Св=0,1 а3.кЯвсов, где а3.к^>1, на этом основании можно написать:
О 5 Tg 6ф
Аз. к*ф
Коэффициент затухания колебаний р3. к, характеризующий диссипативные свойства среды, зависит от амплитуды колебаний вибратора со и угла сдвига фаз 8ф между деформацией и напряжением, возникающими в це
ментном геле в процессе разрушения в нем структурных связей. Чем меньше жидкой фазы в цементном геле, больше величина то, тем больше сдвиг фаз, поэтому с уменьшением пластической подвижности — О. К-б бетонной смеси, коэффициент затухания гармонических колебаний возрастает. Это подтверждается экспериментальными данными, приведенными в работе [96]. Например, при О. К.б=4 см р3.к=0,096 см~1; а при О. К.б=14см р3.к= = 0,0465 см-1; в среднем для О. К.б от 2 до 4 см р3.к= =0,079 см-1. По этим значениям р3. к и ав=0,1 см можно вычислить tg 9ф при различной пластической подвижности бетонной смеси. Так, при О. К.б от 2 до 4 см tg 8ф= =0,00158 и О. К. б=14 см tgOt^O,00093, в связи с чем угол сдвига фаз 0ф не превышает 5. При подстановке вычисленных значений р3. к в формулу (8.2) можно убедиться в том, что с увеличением р3. к амплитуда колебаний ах в бетонной смеси на расстоянии /?р от вибратора убывает. С другой стороны, по мере увеличения амплитуды колебаний вибратора коэффициент затухания уменьшается, т. е. при больших амплитудах колебания затухают медленнее. Такая закономерность установлена экспериментальным путем в работе [56], в которой показано, что для определенного состава бетонной смеси при сов =50 Гц, р3.к=0,0655; а)в=70,5 Гц р3.к=0,0557 и (ов=100 Гц р3.к=0,0404, т. е. с увеличением частоты <ов (уменьшением амплитуды ав) колебания среды затухают скорее.
Уплотнение коагуляционной структуры цементного геля в бетонной смеси возможно только тогда, когда к нему приложено нормальное давление, способствующее сближению сольватированных частиц цемента и увеличению интенсивности сил притяжения между ними. Под влиянием этого явления возникает компрессия (контракция) объема цементного геля. Она сопровождается от - жатием из него некоторого количества жидкой фазы и при определенных условиях ее перераспределением, т. е. переходом некоторого количества «свободной» жидкости в адсорбционно-связанное состояние. Здесь важно заметить, что нормальное давление, воспринимаемое в бетонной смеси цементным гелем, служит средством для сближения частиц, а уплотнение его структуры является результатом проявления активности внутренних сил притяжения между ними.
В поле действия вибрационных (акустических) колебаний возникает волновое давление, под действием которого в вязкопластических средах (гидрогелях и гидрозолях) частицы более плотные, чем среда, сближаются и коагулируют вследствие активизации сил взаимного притяжения. Для оценки величины волновых давлений в бетонной смеси при уплотнении глубинными вибраторами можно воспользоваться зависимостью*:
Р, В = *УМ/ (8.3)
Где Рв — волновое давление возле корпуса вибратора на расстоянии Ri от его оси.
Коэффициент усиления волновых давлений Ку, учитывающий влияние отраженных волн на величину Рхв, Определяется экспериментальным путем. Нетрудно установить, что выражение (8.3) по своей структуре аналогично формуле, описывающей характер затухания амплитуды колебаний вибратора в бетонной смеси при распространении в ней кольцевых волн [56], а именно:
Е
Это обстоятельство свидетельствует об идентичности закона распределения волновых давлений и амплитуд колебаний в бетонной смеси. В связи с этим представляется также возможным выразить изменение величин волновых давлений по аналогии с зависимостью (8.1) так:
Рхв = КуРве2ав (8.4)
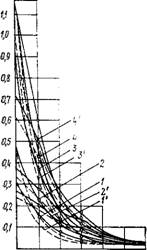
Волновые давления зависят от ширины формы, в которой уплотняют бетонную смесь, частоты колебаний (ов и радиуса распространения вибрации. При этом установлена удовлетворительная сходимость экспериментальных кривых изменения волновых давлений с теоретическими, построенными на основании выражения (8.3). Некоторое различие между этими кривыми (рис. 8.2) обусловливается тем, что в (8.3) учитывается отражение волн только от продольных плоскостей бортов формы,
Формула предложена JT. Ф. Калмыковым.
Между тем как интерференция волн происходит также от торцевых опалубочных бортов и помещенных в бетонную смесь месдоз. В итоге отраженные волны накладываются на падающие, образуя зоны пучности или, наоборот, узлы, в которых волновые давления уменьшаются. Эти явления сопровождается наложением отраженных волн на основные и возникновением вследствие этого стоячих волн, которые в процессе затухания колебательного процесса, отражаясь от продольных бортов формы, сильно искажаются. Описанный волновой механизм значительно усложняет общую картину распространения волновых давлений в бетонной смеси.
|
О 100 200' 300 W 500 600 Rp Расстояние от оси 4и6ратора}ш Рис. 8.2. Изменения волнового давления в бетонной смеси |
|
I «О |
|
1, 2, 3 и 4 — экспериментальные данные при ©£=180; 210; 290 и 300 Гц; 1', 2', 3' и 4' — теоретические данные при таких же значениях O)G. |
Дисперсионный анализ позволил установить, что коэффициент усиления волновых давлений зависит от тех же параметров, что и Рх в, однако на него не влияет состав бетонной смеси. При изменении ширины формы от 500 до 150 мм и (ов=180 Гц Куцоо) возрастает от 1,09 до 1,46; при шв=350 Гц /СУ(5оо) меняется в пределах 1,42— 1,95. Если установлена активная зона распространения вибрационных колебаний в бетонной смеси, тогда в каждом конкретном случае можно принимать РхВ за постоянную величину, равную минимальному его значению в наиболее удаленной от вибратора зоне. В этом случае волновое давление в бетонной смеси будет определяться одним параметром — частотой колебаний вибратора, с увеличением которой волновое давление и эффективность его уплотняющего действия значительно возрастают.
Под влиянием волнового давления в разжиженном цементном геле частицы твердой фазы сближаются, а активность сил их притяжения увеличивается. При частотах вибратора, не превосходящих 50 Гц, отжатия жидкой фазы из цементного геля нормальной густоты практически не происходит; в остальных же случаях, когда (В/Д)г>Кн. г, уплотнение цементного геля сопровождается отслоением жидкой фазы, количество которой с увеличением начального значения (В/Ц)т растет. Физическое состояние цементного геля с разрушенными структурными связями характеризуется условием то=0, при котором нарушается равновесие между внутренними и внешними силами, так как система испытывает избыточное давление Рхв.
Механическая модель объемных деформаций цементного геля при виброуплотнении может быть изображена в виде пружины, имитирующей структурное сопротивление сжатию цементного геля и поршня, оказывающего нормальное давление на жидкую фазу, помещенную в цилиндр с прикрепленной к нему отводящей трубкой. При преодолении сопротивления структуры (разрыве пружины), т. е. разжижении цементного геля, поршень окажет давление на жидкую фазу и она начнет отжиматься через отводящую трубку. В результате этого объем цементного геля уменьшается, т. е. происходит его уплотнение (рис. 8.3,6).
Чем меньше* первоначальная жесткость пружины, тем при меньших частотах вынужденных колебаний произойдет резонанс, слабее окажется структурное сопротивление волновому давлению и тем больше жидкой фазы будет вытеснено из цементного геля. При разжижении большая часть адсорбционно-связанной жидкости будет находиться кратковременно в «свободном» состоянии, поэтому при сравнительно небольшом волновом давлении может достигаться высокая плотность упаковки частиц цемента. В процессе вибрационного воздействия с частотой порядка 100—200 Гц волновое давление (Рхв~ «0,028 МПа) будет восприниматься «свободной» жидкостью и по мере ее отжатия цементные частицы, как бы взвешенные в ней, сблизятся на расстояние, обусловленное равновесием сил притяжения и отталкивания. В связи с этим произойдет дополнительная контракция объема цементного геля, снизится пористость и увели-
Рис. 8.3. Механическая модель объемных деформаций цементного геля
|
Wo |
|
Вя |
|
Ш |
А — до вибрационного воздействия; б — в процессе виброуплотнения
IriunnrmmnhrbtfrnrRr,
Чится плотность его структуры. При прессовании большая часть энергии от статически приложенного нормального давления расходуется на преодоление структурного сопротивления цементного геля сжатию, т. е. редеформа - цию структуры ориентированных молекул жидкости вокруг частиц цемента, и меньшая доля энергии расходуется на отжатие ее из цементного геля.
В разжиженном цементном геле волновое давление затрачивается только на сближение частиц цемента, взвешенных в жидкой фазе, поскольку редеформация структуры молекул жидкости произошла уже под действием резонансной частоты вцбрации. Отсюда следует, что при высокочастотном вибрированном воздействии может быть достигнута такая же плотность структуры цементного геля, как и при прессовании под давлением.
Учитывая указанное отличие виброуплотнения от прессования, относительные деформации и значения (В/Ц) ост цементного геля при вибрационном воздействии можно определить по уравнениям (4.30) и (4.31) при то=0 и yFh=PXB-
_ его-С А, 1,216 /п ( п ч / Р0 ума
|
1,216 |
Их •
1,216 Г / Р0 o. i8
(8.5)
1 его
Р„ �.18
"(8.6)
В зависимости (8.5) и (8.6) подставляют: при Рхв < <0,065 МПа и (В/Ц) гнач>Ка.Г, С=егн; при Рх > >0,065 МПа и (В/Ц) £ач Ж*.Г, С=0,245 и при В/Ц^ </Сн. г, С=0,133.
По формулам (7.23) —(7.28) можно вычислить объемные массы виброуплотненного бетона при различных значениях (В/Ц)нлч. В качестве примера возьмем (В/Ц)*п =0,5, примем Dc=0,75 и 73=2,6 т/м3:
|
= ■ |
1—0,89
При начальном расходе цемента 307 кг/м3, J=l,65 и ри=2,45 т/м3 относительный объем цементного геля Р—0,25. Тогда, согласно зависимости (7.23), получаем Арк = 0,25 (0,231 — 1) =— 0,192.
Относительный объем виброуплотненного цементного геля будет равен
Ру = 0,25 (1 —0,192) = 0,202.
Следовательно, в результате отжатия жидкой фазы объем цементного геля уменьшится на 18%. Для полной реализации эффекта от виброуплотнения бетонной смеси необходимо соответственное увеличение расхода цемента до 342 кг/м3. В этом случае объемная масса све - жеотформованного бетона составит:
2 45 П 4- 0 45)
' i + os9 =1,87 Т/М3 И = 0,75-2,6+ 1,87-0,25 = = 2,422 т/м3.
Из приведенных данных видно, что когда уплотнение бетонной смеси сопровождается дополнительной контракцией объема цементного геля вследствие отжатия, перераспределения жидкой фазы или одновременного их протекания, надлежащей плотности бетона можно достичь, если межзерновое пространство заполнено уплотненным цементным гелем. Это условие диктуется еще и тем, что при данной активности цемента и свойствах заполнителя прочность бетона предопределяется (В/Ц)0ст Бетонной смеси и объемом цементного геля, соответствующим объему пустот смеси заполнителя.
Поскольку при отжатии жидкой фазы под влиянием волнового давления прочность бетона возрастает меньше, чем расход цемента, вязкопластические бетонные смеси уплотнять вибрированием нецелесообразно. В результате отжатия некоторого объема жидкой фазы из цементного геля еще не достигается наиболее выгодное в энергетическом отношении взаимное расположение частиц цемента. С увеличением скорости деформации до величины, обусловливающей дезагрегацию флокул, в цементном геле возникают дополнительные физико - химические процессы, связанные с перегруппировкой частиц и перераспределением жидкой фазы. В связи с этим возрастает дисперсность твердой фазы, перераспределяется жидкость в цементном геле, изменяется его объем и увеличивается водоудерживаюшая способность цемента,
Определим изменение объема цементного геля на следующем примере: при Dc=0,75; v3=2,6 т/м3; (В/Ц) нач = = 0,28 (при Кн. г=0,28); ри=2,59 т/м3; ег0=0,514 начальный расход цемента составит 430 кг/м3. После виброобработки с частотой со =100 Гц вследствие перераспределения жидкой фазы ег= 1/1,66-2,59-0,28=0,437:
1— 0,437 Л _
Dr =---------- !---- = 0,65;
Г 1—0,133
Дрк = 0,25 (0,65 — 1) =—0,0876; ру = 0,25 (1 — 0,0876) = 0,228.
В результате перераспределения жидкой фазы объем цементного геля уменьшается на 9%, в связи с чем расход цемента по формуле (1.18) при (5=0,272 составит
0,272-1000 ^ , Q
Ц =------------- !—------------------ = 466 кг/м3.
М 1/2,59 + 0,28 (1 — 0,292)
Примерно аналогичный результат может быть получен по формуле (1.23) при р=0,25:
Jj 0,25-1000 з
Ц =------------------------------------ = 452 кг/м3.
4 1/2,59 + 0,28(1 —0,396)
В соответствии с приведенными расчетами объемная масса бетонной смеси при виброуплотнении с частотами 50 и 100 Гц выразится следующими значениями:
1. При уплотнении с частотой 50 Гц:
2,59(1 +0,28) т/м3; 0,75-2,6 + 0,25-2,18 =
I + и,514
= 2,495 т/м3;
2) При высокочастотном уплотнении, сов=100 Гц и 2,59(1 + 0,28)
Тг = До 437 = 2,3 Т/М'3; 76 = °'75'2'6 + 0,25-2,3 = = 2,53 т/м3.
Такое же значение уб получаем при р = 0,272 и (В/Ц)*ац = =0,28, а именно:
Тб = 0,75-2,6 + 0,272-2,18 = 2,53 т/м3.
При высокочастотном виброуплотнении бетонной смеси объемная масса его возрастает в 1,015 раза, а цементного геля увеличивается в 1,055 раза. Как это будет далее показано, вычисленные значения объемных масс полностью совпадают с экспериментальными данными.
Таким образом, подтверждается высказанное положение о том что при перераспределении жидкой фазы в цементном геле с минимальным ее содержанием, т. е. при (ВЩ) достигается более ощутимый эффект
От виброуплотнения, чем при отжатии жидкой фазы. Сравнивая значения 7Г и 75 после высокочастотного виброуплотнения с прессованием под давлением 2 МПа, можно убедиться в том, что в обоих случаях достигается примерно одинаковая по плотности структура цементного геля, несмотря на значительную разницу в величинах нормального давления при прессовании и высокочастотном вибрировании. Причина кроется в том, что в разжиженном вибрацией цементном геле создаются благоприятные условия для сближения и взаимодействия частиц, так как на преодоление внутреннего сопротивления сжатию (сил отталкивания) цементного геля, связанного с редеформированием адсорбционно-ориен - тированной дипольной структурой молекул жидкой фазы (воды), не затрачивается львиная доля энергии от внешней нормальной нагрузки. Кроме того, при разжижении цементного геля, полностью нарушается ориентация двойного электрического слоя, препятствующего проявлению потенциальных сил притяжения частиц.
Учитывая при всем этом увеличение дисперсности твердой фазы (от дезагрегации цементных флокул), количества адсорбционно связанной жидкости и равномерное ее распределение в цементном геле, можно считать вполне обоснованными доводы о формировании равноплотных коагуляционных структур при высокочастотном вибрировании и прессовании под определенным нормальным давлением.
Отсюда напрашивается следующий общий вывод: структура цементного геля после уплотнения его механическим воздействием зависит от сил сцепления между частицами твердой фазы, обусловленных главным образом формой связи и структурой молекул жидкой фазы при равномерном ее распределении между частицами цемента/ Остаточное водоцементное отношение может служить параметром плотности цементного геля при соответствующем учете изменения соотношения между «свободной» и адсорбционно-связанной жидкостью после механического воздействия на бетонную смесь.

 Опубликовано в
Опубликовано в