Выбор плана эксперимента и его проведение
 4 июля, 2016
4 июля, 2016  admin
admin Если необходимо изучить модель процесса, определить значимость факторов и их взаимодействий, то можно использовать методы полного и дробного факторного эксперимента (ПФЭ и ДФЭ).
Метод ПФЭ целесообразно использовать, если количество исследуемых факторов не больше трех-четырех. Оптимизацию в этом случае осуществляют по методам Гаусса — Зайделя, методу градиента или крутого восхождения.
В случае исследования влияния режимов пайки и давления наряду с конструкционными факторами модель процесса усложняется, число взаимодействий увеличивается и использовать ДФЭ затруднительно, а ПФЭ — нецелесообразно из-за слишком большого числа опытов. В этом случае можно использовать метод симплексной оптимизации, позволяющий найти оптимальный режим пайки при очень большом числе факторов и минимальном числе опытов.
При исследовании качественных факторов вместе с количественными можно применять сложные совмещенные планы. Эксперимент, обработку его результатов, оптимизацию осуществляют по типовым схемам [75, 76].
После нахождения области определений факторов, их уровней и интервалов варьирования, определения метода оптимизации строят матрицу планирования эксперимента, устанавливают число повторных (параллельных) опытов, проводят рандомизацию. После этого выполняют эксперимент и обрабатывают. его результаты. Для методов ПФЭ и ДФЭ обработку результатов ведут по схеме; проверка воспроизводимости, вычисление коэффициентов регрессии, проверка значимости коэффициентов, проверка адекватности модели н интерпретации полученных результатов.
Затем проводят оптимизацию, т. е. поиск наилучших условий процесса, например, методом крутого восхождения. Для симплексного метода оптимизации обработка данных эксперимента заключается в отбросе наихудшЬх результатов, построении нового симплекса и т. д.
Для сложных совмещенных планов обработка результатов начинается с нахождения оптимального уровни качественного фактора (факторов), дальнейшая схема аналогична ПФЭ и ДФЭ.
Если в результате оптимизации значение критерии удовлетворяет требованиям, предъявляемым к эксплуатационным характеристикам паяного соединении, то исследование закончено, задача решена. Значения факторов, соответствующих иаилучшему критерию оптимизации, также оптимальны.
Пример 1. Применение метода симплексного планирования при нахождении оптимальных режимов композиционной пайки.
Исследовали влияние восьми факторов иа прочность паяного соединения. Критерием прочности паяного соединения (критерий оптимизации) выбрано временное сопротивление разрыву (ов, МГ1а).
Введем обозначения: Jfi — температура пайки; Х2 — температура гомогенизации; Х3 — скорость нагрева паяного соединения до температуры плавления припоя; Xt — скорость нагрева паяного соединения от температуры плавления припоя до температуры пайки; Хъ — давление; Хй— содержание наполнителя в припое; Х2— время выдержки при температуре пайки; Хв — время гомогенизации. Пайка композиционная, вакуумная, печная. Образцы из сплава ОТ4 паяли втавр. Зазор между паяемыми поверхностями изменяли от 0,8 до 1,5 мм. В качестве припоя применяли эвтектический сплав (49% Си—51% Zr) с температурой плавления 877 °С. В качестве наполнителя применяли титановый порошок ПТС дисперсностью 80— 100 мкм. Расплавление легкоплавкой составляющей припоя и смачивание ею тугоплавких частиц происходят во времени, поэтому до температуры плавлення припоя образцы нагревали со скоростью »і, а до температуры пайки — со скоростью v2. Образцы фиксировали в приспособлении и паяли в вакуумной печи (вакуум ~1мПа).
 Область определения, основной уровень и интервалы варьиро-
Область определения, основной уровень и интервалы варьиро-
Выбор плана эксперимента и построение матрицы планирования. Количество факторов — восемь. Вид модели неизвестен. Априорно можно предположить, что будут иметь место многие двойные и тройные взаимодействия. Построить дробную реплику, при которой главные эффекты будут смешаны с априорно не имеющими место взаимодействиями не представляется возможным. При ПФЭ число опытов слишком велико: 2®=512. Выбираем метод симплексной оптимизации.
Преимущества метода — небольшое число опытов, однако этот метод не позволяет описать область оптимума, построить модель процесса, оценить значимость отдельных факторов их взаимодействия.
Принцип симплексного планирования состоит в том, что условия первой серии опытов соответствуют координатам точек, образующих правильный симплекс, состоящий из К+1 точек, расположенных на равном расстоянии друг от друга, в /(-мерном пространстве, где А — число факторов. При этом в одномерном - пространстве (один фактор) симплекс—это отрезок прямой, при двух факторах— равносторонний треугольник, при трех — тетраэдр и т. д. Затем этот симплекс перемещают (кантуют) по поверхности отклика в следующей последовательности.
Из опытов первой се'рии (вер* шииы симплекса) выбирают точку с наихудшим результатом. Определяют координаты новой точки, представляющей собой зеркальное отражение точки с наихудшим результатом относительно противоположной" грани симплекса. При замене точки с наихудшим результатом новой точкой образуется новый симплекс, смещенный (в общем случае) в сторону лучшего результата. В этой новой точке вновь ставят опыт. Выбирают опять иаихудшнй результат, находят его зеркальное отображение и т. д. Так, симплекс перемещают до тех пор, пока ие будет достигнута область оптимума. Если две точки имеют одинаковый иаихудшнй результат, то решение об отбросе одной из них принимают случайным образом. Если значение критерия оптимизации во вновь определенной точке (вершине) вновь окажется минимальным, то отбрасывают вершниу со следующим по порядку минимальным значением.
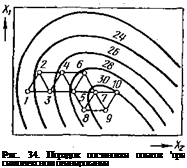 На рис. 34 изображен порядок постановки опытов при симплексном планировании. В первой серии ставят k+l опыт (точки 1, 2; 3). Последующее перемещение симплекса осуществляют с учетом полученных результатов. В точке 1 получен наихудший результат. Симплекс поворачивают вокруг грани 2—3, в точке 4 ставят опыт. Далее анализируют результаты опытов в точках 2, 3 и 4. Отбрасывают результат точки 2 (иаихудшнй) и поворачивают симплекс вокруг грани 3—4. Определяют координаты точки 5, в которой снова ставят опыт и т. д.
На рис. 34 изображен порядок постановки опытов при симплексном планировании. В первой серии ставят k+l опыт (точки 1, 2; 3). Последующее перемещение симплекса осуществляют с учетом полученных результатов. В точке 1 получен наихудший результат. Симплекс поворачивают вокруг грани 2—3, в точке 4 ставят опыт. Далее анализируют результаты опытов в точках 2, 3 и 4. Отбрасывают результат точки 2 (иаихудшнй) и поворачивают симплекс вокруг грани 3—4. Определяют координаты точки 5, в которой снова ставят опыт и т. д.
Критерием выхода в район оптимума служит прекращение поступательного движения' симплекса, он начинает вращаться вокруг одной из вершин: например, значения в последовательно отбрасываемых точках 8, 9, 10 ие превышают значения в точке 7_с наилуч- шнм результатом, вокруг которой вращается симплекс.
Выбрано число параллельных опытов: /л=3. Рассчитаны значения факторов в первой серии из девяти опытов. Опыты рандомизированы. Построена матрица исходного симплекса, получены результаты опытов (табл. 87). Результат каждого опыта есть среднее арифметическое трех повторных опытов. Значения факторов округляли, учитывая точность их фиксирования. При этом значения факторов не должны выходить за границы области их определения. Например, параметр Хъ в- первых пяти опытах имеет значение: ^б(,-й=Х0 4-ДАГБаБ=30+10-0,129=31,3, в шестом опыте X6,6=-Xg + +АХЪ(—РЪ)=30—10-0,645= 23,5, в остальных ■A’5(7_9)=A'J? +0=30.
Аналогично получены значения других факторов. Значения A-факторов в первой серии из К+1 опытов находят из выражения Xij—X9+bXiZij, где Xjj — числовое значение t-того фактора в /-том опыте; ДХі интервал варьирования /-того фактора; Дzt3—
координата симплекса для t-того фактора н /-того опыта берется из справочных данных.
|
Номер отброшенного опыта |
Номер опыта _ |
х. |
Xt |
Xt |
X, |
*7 |
х, |
(Y*) МПа |
||
|
* |
і |
1110 |
945 |
11 |
10,5 |
31,3 |
51 |
20,9 |
40,8 |
311 |
|
2 |
1090 |
945 |
11 |
10,5 |
31,3 |
51 |
20,9 |
40,8 |
236 |
|
|
3 |
1100 |
930 |
11 |
10,5 |
31,3 |
51 |
20,9 |
40,8 |
266 |
|
|
4 |
1100 |
940 |
7,5 |
10,5 |
31,3 |
51 |
20,9 |
40,8 |
320 |
|
|
* |
5 |
1100 |
940 |
10 |
7,5 |
31,3 |
51 |
20,9 |
40,8 |
250 |
|
6 |
1100 |
940 |
10 |
10 |
23,5 |
51 |
20,9 |
40,8 |
260 |
|
|
7 |
1100 |
940 |
10 |
10 |
30 |
43,5 |
20,9 |
40,8 |
228 |
|
|
8 |
1100 |
940 |
10 |
10> |
30 |
50 |
14,4 |
40,8 |
315 |
|
|
-9 |
1100 |
940 |
10 |
10 |
30 |
50 |
20 |
33,3 |
276 |
|
|
7 |
10 |
1100 |
940 |
10,0 |
10,0 |
30 |
58,0 |
48,8 |
38,9 |
227 |
|
2 |
11 |
1115 |
935 |
9,0 |
9,5 |
28,4 |
48,5 |
18,8 |
38,9 |
284 |
|
5 |
12 |
,1100 |
940 |
9,5 |
13,0 |
27,7 |
48,0 |
18,3 |
38,6 |
325 |
|
6 |
. 13 |
1110 |
940 |
9,5 |
11,0 |
36,6 |
47,0 |
17,6 |
37,9 |
344 |
|
3 |
14 |
шо |
950 |
8,0 |
10,5 |
30,0 |
46,0 |
16,8 |
37,2 |
288 |
|
9 |
15 |
1115 |
945 |
8,5 |
11,0 |
31,3 |
4,65 |
16,9 |
45,6 |
351 |
|
7 |
16 |
1120 |
945 |
8,0 |
11,5 |
31,6 |
53,5 |
15,0 |
39,3 |
391 |
|
11 |
17 |
11(05 |
950 |
9,0 |
12,5 |
34 |
50 |
16,1 |
41,3 |
391 |
|
14 |
18 |
1110 |
940 |
10 |
12,5 |
33,5 |
53 |
18 |
44 |
352 |
|
1 |
19 |
1110 |
940 |
7 |
12,5 |
32,4 |
49 |
13 |
41,3 |
354 |
|
8 |
20 |
1120 |
945 |
7 |
13 |
35 |
49,5 |
20 |
41,4 |
355 |
|
4 |
21 |
1125 |
950 |
9,5 |
14 |
35 |
49 |
13,8 |
42 |
390 |
|
12 |
22 |
1120 |
950 |
7,5 |
12 |
38 |
51 |
14,3 |
45 |
424 |
|
.13 |
23 |
1125 |
950 |
6,5 |
14 |
31 |
53 |
15 |
47 |
384 |
|
28 |
31 |
1150 |
960 |
6,5 |
14 |
40 |
50 |
15 |
60 |
501 |
|
* Среднее арифметическое трек повторнык опытов. Обработка реэультатов эксперимента. Проверка значимости различий повторных опытов показала их воспроизводимость. Из табл. 87 видно, что в седьмом опыте получена наименьшая прочность, т. е. значение параметра оптимизации минимально. Зеркальное отображение этой точки получено в опыте 10 |
Хцк+2) “• 2ІК(Хіл + Хіл + Xi,3 + ••■+■ Xfrp—i +
X[,p+1... XltK+i —Xt).
где P — номер опыта, в котором значение Y минимально.
Например, - Хмн»=2(51,6+50,2)/8—43,5= 58, т. е. новое значение фактора равно удвоенному среднему арифметическому всех его значений без учета отброшенного минус отброшенное (минимальное) значение. Для фактора Х3 получим
Хз(Ю) = 2(3,11 + 7,5 + 4,10)/8 - 10 и т. д.
Значение параметра оптимизации Ую вновь оказалось минимальным. Результаты опыта' 10 исключаем из дальнейших расчетов. Возвращаемся к исходному симплексу и отбрасываем вершину со следующим по порядку минимальным значением — опыт 2.
Находим значения факторов в:опыте 11. Например:
; . Х6(10) - 2 (51,5 + 43,5 + 50.2)/8 — 51 - 48,5 и т. д.
Получаем новый симплекс, в котором опыт 2 заменен опытом 1.1 н т. д. Аналогично рассчитываем значения факторов в последующих опытах. Опыт 7 вторично отбрасывали в опыте 16.
Результаты,- эксперимента. Наилучшее значение критерия оптимизации (с»=501 МПа) получено в опыте 31. Значения Y в последующих пяти опытах ие превышают значення, полученного в опыте 31, т. е. симплекс начал свое вращение вокруг этой точки.
Пример 2. Применение полного факторного - эксперимента при нахождении оптимальных режимов контактно-реактивной диффузионной пайки сплава ОТ4. - -
Изучали механические свойства паяных иахлесточиых соединений. Критерием оптимизации была выбрана кратковременная прочность паяного соединения на срез тСр, МПа, при 2(гС. Цель эксперимента— исследование влияния на прочность соединения следующих факторов режима пайки: Х{— температура пайки, °С; Х2— выдержки при температуре пайки, мин; Х3 — толщина покрытия припоя, мкм.
Способ пайки:—контактно-реактивная диффузионная пайка; в качестве контактного покрытия использовали никель. Пайку проводили в вакуумной печн, при температуре пайки вакуум —0,01 Па.
Припой в виде покрытия наносили на одну из паяемых пластин. В процессе Пайки к паяемым поверхностям прикладывали небольшое Давление. . Скорость нагрева образцов регулировали мощностью установки, паяное соединение охлаждали вместе с печью. Поверхности перед пайкой были очищены н протравлены. Величину нахлестки регламентировали конструкцией изделия.
' Область определения, основной уровень и интервалы ', варьирования факторов. Фактор X,. Учитывая температурные интервалы недопустимого роста зерна в сплаве ОТ4, начала контактно-реактивного плавления титана с никелем, устойчивого существования ии - терметаллидов, температуры рекристаллизации паяемого материала, была выбрана область определения для температурного интервала пайки от-950 до 1050°С.
Фактор Х2. Учитывая время до начала недопустимого роста зерна сплава ОТ4 при температуре пайки н образования прослойки жидкой фазы в контакте с припоем, выбрана область определения для времени выдержки при температуре пайки от 0 до 240 с.
На основе априорной информации и предварительных экспериментов были выбраны основные уровни и интервалы варьирования факторов:
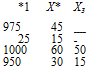 Основной уровень. . Интервал варьирования Верхний уровень. . Нижний уровень. .
Основной уровень. . Интервал варьирования Верхний уровень. . Нижний уровень. .
Выбор плана эксперимента и построение матрицы планирования. Число факторов — три. Вид модели неизвестен. Выбираем полный факторный эксперимент. Тогда вид модели — неполная ква-
|
Номер опыта |
X, |
X, |
X, |
Х, Хе |
Х, х„ |
ХяХ» |
Х, ХгХ, |
|
і |
+ |
+ |
+ |
.+ |
+ |
,ф |
+ |
|
2 |
--- --- |
+ |
+ |
— |
— |
.+ |
|
|
3 |
+ |
— |
+ |
— |
+ |
— |
1------------- |
|
4 |
— |
•— |
+ |
,+ |
—. |
—. |
+ |
|
5 |
+ |
ф |
і_ |
.+ |
— |
—, |
— |
|
6 |
. «н» |
+ |
— |
— |
+ |
— |
Ф |
|
7 |
+ |
— |
1— |
— |
—. |
ф |
Ф |
|
8 |
— |
— |
+ |
+ |
— |
|
Примеча н н е. Знак «+» — значение верхнего уровня фактора, знак «—» — значение нижнего уровня фактора. |
|
Таблица 89. Порядок проведения и результаты опытов
|
дратичная, с учетом всех взаимодействий факторов. Матрица планирования приведена в табл. 88.
Переход от натуральных значений факторов к кодированным значениям задается формулами:
О О *i — 975 с - *2-45
■ <=~ДЛГ": ‘"1 _ 25 ' 15 *
Например: *imax= (1000—975)/25= + 1; *imin=(950—975)/25=
Рассчитано число повторных опытов. Из предварительных экспериментов были определены коэффициент вариации у=0,03; допуск Да=0,05. Находим число повторных опытов: оно равно трем.
Рандомизация. Чтобы исключить влияние систематических ошибок, вызванных внешними условиями (например, изменение среды), т. е. при постановке опытов, запланированных матрицей, выбрана случайная их последовательность. Общее число опытов 24. Получаем последовательность проведения опытов по таблице случайных чисел. Из произвольного места таблицы случайных чисел выписы-
дают. числа. , Например, при 24 опытах c l по 24, с отбрасыванием уже' выписанных. В табл. 89 приведены порядок выполнения опытов и их результаты (Ун К* и У* — результаты трех повторных опыт тов,"У—среднее значение).
Таким образом, первым реализуется опыт 7, вторым опыт 5
и Т. Д. - , -
Обработка результатов экспериментов. Проверка значимости различий повторных опытов показала значимость всех опытов.
Для проверки воспроизводимости результатов подсчитывали дисперсии в каждой строке матрицы (табл. 90) по формуле: S2* =■
I я»
— ------- (Уде—-Уд)*, где <=1,2, .... N — номер опыта (стро-
* . 9—1
ки); о=1, 2, , m — номер среднего арифметического.
Гипотеза об однородности дисперсий проверяется с помощью
8
критерия Кохрена: Орасч “ S2ymax / 2 “ 0,089/0,228 = 0,43.
і
Для степеней свободы /<=т—1=2 и f*=!V=8 табличное значение критерии равно 0,516 (а=0,05). Гипотеза об однородности дисперсий принимается.
Если проверка на однородность дала отрицательный результат* то остается признать невоспроизводимость экспериментальных данных вследствие наличия неучтенных факторов, произвольно изменяющихся от опыта к опыту, несовершенства методики эксперимента и т. д. При этом следует увеличить число повторных опытов* включить в план новые факторы, усовершенствовать методику и т. д. Определяют дисперсию воспроизводимости, как среднее ариф-
метическое всех дисперсий: ^ {у} =2 S2//® = 0,228/8 = 0,026.
і
|
Таблица 90. Дисперсии среднего арифметического
|
а
Итого: 0^28= 2 s/
1-і
2 г - г г
Примечание. Sy-Дді+Дя +Ддз(Зт-1),.
Число степеней свободы этой дисперсии N(m— 1J—18. Вычие-
1 N ■ _
ленив иоэффициеитов регрессии Ы — 2 XjiYi:
” і-1
Ь0 = (31,93 +26 +28,43 +23,1+ 35 +32,37+ 31+28,77)/8 =29,59; Ьх =(31,93 —26 +28,43 -23,1+ 35 -32,47+31—28,77)/8 = 2,0;
Ь2 = (31,93 +26 —28,43 - 23,1 +35 +32,47-31—28,77)/8 = 1,76; Ьг = (31,93 +26 +28,43 +23,1-35 -32,37—31-28,77)/8 = - 2,221 *12 « (31,93 -26 —28,43 +23,1 +35 — 32,47-31 + 28,27.)/8 = 0,11; й13 = (31,93 —26 +28,43 —23,1 -35 +32,47— 31+ 28,77)/8 = 0,81
*аз = (31,93 +26 -28,43—23,1-35 -32,47+31+28,77)/8 -------------- 0,16;
*ш “ (31.93 -26 — 28,43 +23,1—35 +32,47+31—28,77)/8 = 0,04.
Проверка значимости коэффициентов. Дисперсия ошибки определения коэффициентов Ьіі
} = S| у} INm = 0,026/8 • 3 = 0,001;
S{fti} - (S2{M ) ,/a = (0,001),/.=0,033 .
Гипотезу о значимости коэффициентов регрессии проверяют е вюмощью /-критерия Стьюдеита: /i=|*i|/5j^j.
При f=N(m—1) = 16 степеням свободы (а=0,05) табличное значение /-критерия равно 2,119;
/, = 2,0/0,033 = 60,76; /1а = 0,11/0,033 = 3,34;
/2 = 1,76/0,033 = 53,47; tn = 0,81/0,033 = 24,61;
/8 = 2,22/0,033 = 67,45; /» - 0,16/0,033 = 4,86; tm = 0,04/0,033 = 1,21.
Если найденная величина параметра /і>/таел при данных f и <к, то коэффициент Ьг признается значимым. Значимыми оказались ice главные эффекты и эффекты парных взаимодействий, эффект Тройного взаимодействия (л, Х2 Х3) оказался незначимым, т. е. равным нулю, так как /ш</тавл-
Незначимость коэффициента Ьх может быть обусловлена следующими причинами: точка оптимума близка, шаг варьирования АХ і выбран малым, ошибка эксперимента вследствие неучтенных факторов велика; данный фактор не связан функционально с критерием оптимизации, т. е. действительно равен нулю.
Следовательно, математическая модель процесса имеет вид:
Г- 29,59 +2Л+1,76*2 —2,22*3 + О. И^Х* +0,8X1A,3 - О. ІбЛу^.
Проверка адекватности модели. По полученному уравнению регрессии вычисляют значения У в условиях каждого из восьми опытов, т. е, предсказанное вначение Фр
^ -29,59 + 2+ 1,76 - 2,22 + 0,11 + 0,81 — 0,16 - 31,89; £ - 29,59 — 2 + 1,76 — 2,22 — 0,11 - 0,81 - 0,16 - 26,03 { £ - 29,59 + 2 - 1,76 — 2,22 - 0,11 + 0,81 + 0,16 - 28,47; Yt - 29,59 — 2 — 1.76 — 2,22 — 0.11 - 0,81 + 0,16 - 23,07; Ya - 29,59 + 2 + 1,76 + 2,22 + 0,11 - 0,81 + 0,16 - 35,03; У* - 29,59 -2 + 1,76 + 2,22 — 0,11 + 0,81 + 0,16 - 32,43; £ - 29,59 + 2 — 1,76 + 2,22 — 0,11 - 0,81 — 0,16 =. 30,97; £ - 29,59 — 2 —1,76 + 2,22 + 0,11 + 0.81 — 0,16 - 28,81.
Определяют разницу между экспериментальными (см. табл.
и вычисленными значеннями Y или невязку Л У*. Невязка показым#- отклонеиие между експериментальними и вычисленными по у рал нению регрессии значениями У в /-той экспериментальной точкД
Др, - (31,93 — 31,891 -0,04; ДУ» - |35,0 — 35,03|- 0,03; д£ — (26,0 - 26,051 -0,05; Д £ - |32,47 — 32,43| - 0,04;
ДУ, - 128,43 — 28,471 - 0,04; &9Г - |31,0 — 30,97| -0,03;
ДУ4 - 123,1 - 23,07| - 0,03; а9, - |28,77 — 28,811 - 0,04.
Определяют дисперсию адекватности:
|
0,04» + 0,08»+•••+0,03»-0,04* |
![]()
![]() N — d
N — d
где d — число членов найденного полинома с учетом свободного * л
члена; ^ ДУ5; —сумма квадратов всех иевязок; rf—7.
і
Проверяют гипотезу об адекватности модели с помощью ^-критерии ФнШераї
FptC4 - S2M/Sf у] =» 0,0116/0,026 - 0,446.
При числе степеней свободы fі *=N—d—1 и ft—N(m—1) —IS табличное значение /•'-критерия равно 4,49.
/гра«ч</гтавл, т. е. гипотеза об адекватности модели принимается.
Необходимо отметить, что адекватность данной модели сразу была очевидна, так как табличные значения критерии Фишера всегда больше единицы, т. е. математическая модель адекватно представляет объект для любого числа степеней свободы f и /2.
Проверка адекватности возможна при /а. д— /V—-d>0, если W—
=d, проверить адекватность модели невозможно. Неадекватность ■модели может быть вызвана следующими причинами: велик шаг варьирования, основной уровень выбран далеко от центра Области ■определения, не учтены значимые эффекты, взаимодействия, модель действительно неадекватна, т. е. надо переходить к более сложной форме модели или к другому методу планирования.
Интерпретация результатов. Все линейные эффекты значимы, т. е. все исследуемые факторы (температура пайки, время выдержки и зазор) оказывают существенное влияние на предел прочности паяного соединения при срезе. Из уравнения (10) видно, что иаи - - болынее влияние оказывает Х3 — толщина покрытия (зазор) (£>а=— —2,22), далее следует X]—температура пайки ("-бі=2,0) и затем Хг — время выдержки (62= 1,76). Таким образом, можно написать следующий ранжированный ряд для линейных эффектов: Ь3>Ь> ^ Ъ%. (
'' Знак коэффициента Ь указывает, как влияет фактор на результат опыта. - С увеличением всех факторов, кроме толщины покрытая, прочность -'паиного соединения при срезе увеличивается и наоборот.
Эффекты взаимодействия составляют нелинейную часть уравнения (10). Смысл этого эффекта состоит в том, что"действие фактора зависит от того, на каком уровне находится другой фактор. В уравнении (10) значимы все взаимодействия первого порядка, но их влияние невелико по сравнению с главными эффектами; Ьіз-«0,11; ■прочность (У) будет увеличиваться с увеличением температуры пай - . жи и времени выдержки и наоборот. £>i3=0,81; оба фактора действуют также в одном направлении. £>23=—0,16; увеличивается с увеличением времени выдержки (1>2>0) и уменьшением толщины прокладки припоя (6в<0) и наоборот.
Крутое восхождение. Изменяя независимые переменные пропор - ниоиалыю величинам коэффициентов регрессии, совершают движение в направлении градиента функции отлика по самому короткому (крутому) пути к вершине — оптимуму. Рассчитывают составляющие градиента, определяют шаг движения по градиенту и проводят новую серию опытов.
Фактор, для которого произведение £><АХ< максимально, принимают за‘базовый, для него выбирают шаг движения по градиенту, ■оставляя старый или вводя более мелкий. Шаг Кі может быть как ■больше, так л меньше нуля. Нижняя граница шага должна позволять фиксировать два соседних опыта, верхняя — область определения фактора. Если при восхождении достигается граница области определения одного из факторов, то следует зафиксировать значение этого фактора и дальше двигаться по остальным. Крутое восхождение эффективно, если хотя бы одни результат лучше иаилуч - лнего в серии.
Значение фактора Хз при крутом восхождении приняли равным 15 мкм, т. е. по нижйему уровню, так как уменьшение этого фактора приводит К увеличению параметра оптимизации (£>з«* =-2,22).
При крутом восхождении фактор Хі достиг границы области определения в опыте 11, это значение было зафиксировано, далее двигались по фактору Хз.
Ниже приведены данные, характеризующие условия движения по градиенту при оптимизации режимов контактно-реактивной пайКЙ сплава ОТ4 с припоем на основе никеля:
Ai Xj
Основной уровень................................................... 975 45
Интервал варьирования........................................... 25 15
Коэффициент регрессии bt............................ 2 1,76
Составляющая градиента Аі=ЬіАХі. . 50 26,4
Шаг при изменении Хі в два раза Кі=Аіі2................ 25 13,2
Округление шага....................................................... 25 15
Крутое восхождение оказалось эффективным. Значения отклика У(тс. р, МПа — среднее трех повторных опытов) в новой серии опытов приведены ниже:
|
Номер опыта |
X, |
хг |
Y |
|
9 |
1000 |
60 |
____ |
|
10 |
1025 |
75 |
36,4 |
|
11 |
1050 |
90 |
— |
|
12 |
1050 |
105 |
39,2 |
|
13 |
1050 |
120 |
39,4 |
|
14 |
1050 |
135 |
39,3 |
|
15 |
1050 |
150 |
38,7 |
|
16 |
1050 |
165 |
38,2 |
Наибольшее значение прочности иа срез достигнуто в опытах 12—14. Область оптимума достигнута. Исследование можно прекратить.
Результаты экспериментов. Было получено максимальное значение прочности на срез (тср=392-н394 МПа) при следующих значениях факторов: Хі=1050°С (верхняя граница области определения); Х2=105-н135 мин; Х3=15 мкм.
 Опубликовано в Проектирование технологии пайки металлических изделий
Опубликовано в Проектирование технологии пайки металлических изделий Комментарии закрыты.
