В условиях плазмотрона электрическая дуга движется по окруж­ности, как показано на рис. 8.15. Диаметр электрода D, а также коэффициент конвективного теплообмена на внутренней стенке элек­трода а будем считать заданными.

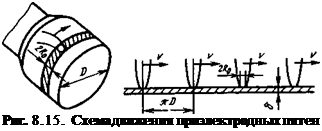Картину многократного пробегания приэлектродного пятна дуги по замкнутой траектории можно представить в виде бесконечного ряда источников, расположенных на расстояниях nD друг от друга и бе­гущих вдоль внешней поверхности плоской стенки с заданной ско­ростью V, как показано на рис. 8.15. Естественно, чем меньше длина траектории irD, тем больше температура нагрева от предыдущих про­беганий дуги.

Можно показать, что при скоростях v > 100 температура от пред­варительного нагрева всеми источниками (Т^) получается прибли­зительно такой же, как в случае действия распределения по кольцу ttD постоянного источника, суммарная интенсивность которого равна интенсивности выделения энергии в приэлектродном пятне, а ширина равна ширине, занимаемой приэлектродными пятнами, 2RQ.

Таким образом, для определения температуры предварительного нагрева будем рассматривать нагрев охлаждаемой стенки электрода от источника в виде ленты шириной 2R^, как показано на рис 8.16.

Следует заметить, что эта ширина 2R^ в значительной мере зависит

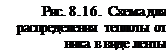от условий горения дуги в каждом конкретном плазмотроне. Пятна могут занимать полосу, ширина которой существенно больше размера пятна. В случае, если траектория дуги достаточно хорошо стаби­лизирована и пятно повторно пробегает по своему следу, то за раз-

мер 2/?0» по-видимому, наиболее правильно принять поперечный размер

дуги d. Это подтверждается сравнением поперечного размера дуги и суммарной ширины следов (см. рис. 3.3). Зависимость этого размера от силы тока, давления и интенсивности магнитного поля дается формулой (3.5).

Будем рассматривать температурное поле в пластине бесконеч­ной длины шириной I и толщиной 6. Боковые поверхности пластины теплоизолированы. На внутренней охлаждаемой поверхности задан коэффициент теплообмена а. На наружной поверхности действует ис-

_2_

и шириной 2/?q. Остальная часть наружной поверхности

X ■ 0 и различных значениях аб/Л

Полученный ряд знакопеременен и в нем достаточно оставить 2...3 члена. Ошибка легко определяется по величине следующего отбра­сываемого члена.

На рис. 8.17 приведены результаты расчетов температуры по фор­муле при различных интенсивностях охлаждения и различной ширине

стенки I = --- . Видно, что в выбранном диапазоне распреде-

ление температур в плоскости симметрии уже при I = 4 соответ­ствует распределению температур в стенке бесконечной ширины. Видно также, что одномерный расчет температуры стенки без учета

’’растекания” тепла, т. е. при / = 1, может приводить к сущест­венному завышению температуры, особенно при слабом охлаждении.

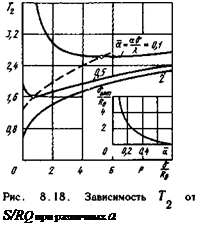
Из анализа зависимости (8.11) можно сделать важный практический вывод, заключающийся в существовании оптимальной толщины стенки при заданной интенсивности охлаждения. На рис. 8.18 приведена за­висимость температуры на наружной поверхности электрода от толщины стенки. Видно, что при слабом охлаждении минимальные зна­чения температуры получаются для стенок достаточно большой тол­щины. Это является результатом бокового ’’растекания” тепла от источника.

Приведем формулу (8.11) в размерном виде

Из полученной зависимости затруднительно без численных расчетов показать влияние силы тока / на температуру Т. Для выяснения этой

^ 8 2

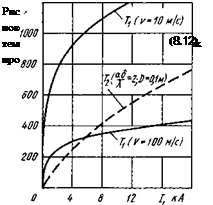
зависимости приведем численный пример при AU = 11 В, / = 10 А/м, =2, D = 0,1 м. Результаты расчета приведены на рис. 8.19. Видно, что температура Т существенно зависит от силы тока.

Для сравнения на рис. 8.19 представлены графики температуры 7^,

показывающие нагрев в пятне. Расчеты проведены по формуле (8.4) при тех же исходных данных и при двух значениях скорости v = 10 м/с и v = 100 м/с. Видно, что для больших значений силы тока температура от предварительных пробеганий дуги становится соиз­меримой с температурой в пятне, а при увеличении скорости может стать преобладающей.

Полученные результаты позволяют выбрать толщину стенки элек­трода, интенсивность его охлаждения, диаметр электрода и необ­ходимую скорость перемещения приэлектродного пятна.