КОЛЕБАНИЯ МОЩНОСТИ. В ТРЕХФАЗНЫХ ЦЕПЯХ. С ЭЛЕКТРИЧЕСКИМИ ДУГАМИ
 17 июля, 2016
17 июля, 2016  admin
admin Вопрос о колебаниях мощности в электродуговых установках в ряде случаев может иметь важное значение. Например, колебания мощности в плазмотронах могут вызвать значительную нестаиионарность выходных параметров, в частности температуры выходящей струи газа. Такие плазмотроны не годятся для целого ряда научных и технических задач. Можно привести и другие примеры, показывающие, что необходимо подробнее рассмотреть этот вопрос. Для однофазных электродуговых устройств колебания мощности всегда будут значительными: мощность равна нулю в точке г = 0, затем достигает максимума и снова снижается до нуля в точке т = я. Однако в трехфазных цепях колебания суммарной мощности могут быть значительно меньше. Известно, что в симметричной трехфазной цепи с линейной нагрузкой (кривые тока и напряжения имеют синусоидальную форму) мгновенное значение суммарной мощности всех трех фаз не зависит от времени, т. е. колебания мощности отсутствуют. Такие цепи называются уравновешенными. В трехфазных цепях с дугами суммарная мощность в общем случае не остается постоянной. Рассмотрим случай, когда дуговые разряды соединены в симметричную "звезду” (для соединения "треугольником” рассмотрение аналогичное). Для простоты считаем
кривые токов синусоидальными. Кривая напряжения на дуге имеет произвольную форму и задана рядом Фурье. Тогда суммарная мощность дуг запишется в следующая виде:
![]()
![]() со г
со г
Z A isin т sin лг + „ л I л-о *•
+ sin (т + - у- )sin |л(г + - у - )j + + sin (г - - у - )sin [л(т + - у - )J|.
Производя преобразования, получим
ОО
Р = Z A (2sin т sin яг sin2 *
л Л 3
л-о
+ ІЗ cos г cos лг sin 2™ ). (7.37)
Из (7.37) следует, что при синусоидальном напряжении А = 1, А = О при л * 1
Я = 4- “ * = 31// = const,
2 тт
т. е. мощность не зависит от времени. Бели напряжение несинусоидально, то в общем случае мощность является функцией времени. Однако не все гармоники дают свой вклад в мощность Р(т). Для гармоник с номерами, кратными трем (л = Злі), Р^ = 0, как видно из
![]()
(7.37). Таким образом, зависимость Р{т) обусловлена гармониками с номерами, не равными 1 и не кратными 3. Тогда (7.37) можно преобразовать к следующему виду:
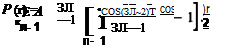 |
|
Бели обозначить через Р колебательную мощность, то получим
Формула (7.38) позволяет найти колебательную составляющую мощности для любой формы напряжения на дуге.
В качестве примера рассмотрим случай, когда кривая напряжения дуги имеет прямоугольную форму. Можно вычислить Р(т) по (7.38),
однако в данном случае удобнее найти эту зависимость графическим путем. Очевидно, что мощность каждой фазы равна |sin т|, а углы сдвига кривых мощности каждой фазы относительно двух других равны ± эт/3. Складывая мгновенные значения мощности всех трех фаз, получим Р(т). Выполнив соответствующее построение, заметим, что суммарная мощность колеблется с частотой, в три раза большей, чем частота колебаний мощности в одной фазе (для частоты сети 50 Гц частота колебаний мощности одной фазы равна 100 Гц, а частота колебаний суммарной мощности - 300 Гц). Максимальное отклонение суммарной мощности от среднего значения не гревышает 7 %. Таким образом, колебания мощности при прямоугольной форме кривой напряжения дуги относительно невелики.

 Опубликовано в
Опубликовано в