Второй метод
 16 июня, 2016
16 июня, 2016  admin
admin В этом методе, как и в предыдущем, на каждый электрод наматываются две катушки, через одну из которых пропускается ток данной фазы. Вторая катушка замкнута на конденсатор (рис. 6.15). Вследствие смещения фазы тока во второй катушке но отношению к первой, обусловленного включением конденсатора, удается получить результирующее магнитное поле с фазовым сдвигом р. Это видно из следующего приближенного расчета.
Пусть d, * d2 * dQ.
Тогда HI = /Qtt>0 + + l2W2' (6.14)
Наводимая ЭДС (x - индуктивное сопротивление)
E = - jxHbaT1,
откуда с учетом того, что о» - 1, а дг^ * 1/ссС, получаем /( = = “ jx^Hl/R^ (в электроде);
I = Е/1Л ------------- - р,—:—— (во второй катушке).
2 2 2 а» (Л -/*£>
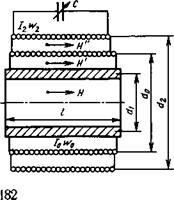 Рис. 6.15. К расчету напряженности
Рис. 6.15. К расчету напряженности
магнитного поля и фазового сдвига в
системе с двумя катушками и конден-
сатором
Подставляя полученные выражения в (6.14) и учитывая, что /Qia»0 = = HI, получим
![]() = [і ♦ /у*, ♦ /у<*2 - /у] •
= [і ♦ /у*, ♦ /у<*2 - /у] •
Рассмотрим сначала случай R. < хг. Обозначая х,/Я, = а, и х! хп -
2 С 1 1 1 2 С
= получим
Н/Н0 = (1 - а2 + /а, Г1,
откуда
/////0 = [(1 - а/ ♦ а*] 1/2; (6.15)
![]() tg = - уа - а2).
tg = - уа - а2).
Формула (6.16) указывает на принципиальную возможность регулирования фазового сдвига в пределах > - п, где <f>Q - фа
зовый сдвиг при разомкнутой второй катушке; это соответствует изменению а2 в пределах 0 < < оо. формула (6.15) указывает также
на возможность усиления поля в полости электрода по сравнению с приложенным. Действительно, если а < 1, то в некотором диапазоне
изменения а имеет место соотношение Н > /Л. Это объясняется ре-
зонансными явлениями в рассматриваемой системе. Эксперименты по схеме, аналогичной приведенной на рис. 6.8, подтвердили возможность регулирования фазового сдвига с помощью емкости и получать при этом усиление магнитного поля в полости электрода, однако
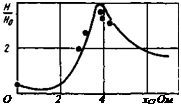 Рис. 6.16. Зависимость напряженности магнитного поля от емкости: расчет: • — эксперимент
Рис. 6.16. Зависимость напряженности магнитного поля от емкости: расчет: • — эксперимент
|
|
|
![]()
![]() V'(jrc~V
V'(jrc~V
0 #/
Vyuc“x22)+ai ucVV/7V
|
-2 2—1 где *2 = 0,25м0сли*|Ю;2/ ; |
дг2 = 0,25м0ож(^-^; |
|
■ 0.25«0^(4 - <><*¥ |
0 00 ДГ„„ = хл + ЛГ + X: 22 2 2 2 |
/?2 - активное сопротивление второй катушки.
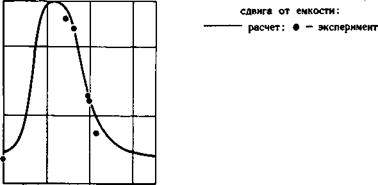
На рис. 6.16 и 6.17 сопоставлены результаты эксперимента и расчета по формуле (6.17), из которых видно их хорошее совпадение. Максимальное значение напряженности магнитного поля в полости электрода почти в 4 раза превышает напряженность поля на внешней поверхности электрода.

 Опубликовано в
Опубликовано в