6.2.1.Оценка допустимого фазового сдвига

С точки зрения стойкости электрода основную опасность пред­ставляет собой тепловой поток в электродном пятне, который может достигать очень больших значений. Для оценки допустимого сдвига фаз рассмотрим сначала задачу о нагреве электрода при неподвижном
пятне дуги переменного тока. Тепловой поток в пятно определяется следующим образом:

q = jAU

В

где AU^ - некоторое эффективное приэлектродное падение напряжения (катодное или анодное).

Ввиду большой сложности происходящих на электродах процессов примем ряд упрощающих предположений.

Будем считать пятно дуги круглым с равномерной плотностью тока в нем и примем, что плотность тока постоянна / = const (не зависит

2

от силы тока дуги). Тогда площадь пятна ттг^ (г^ - радиус пятна)

будет увеличиваться во времени по мере роста мгновенного значения тока *’(/):

яг* = пт

Примем, что і = /^sin о>/ (о> - циклическая частота). Будем рас­сматривать достаточно малый временной интервал (вблизи нуля тока), для которого справедливо приближение sin о>/ - (А (ниже будет по­казано, что даже за это короткое время температура в пятне может превысить температуру плавления). В этом случае

rjj = (6.1)

Рассмотрим задачу о нагреве электрода в следующей постановке (рис. 6.3). На поверхности полуограниченного тела расположен кру­говой тепловой источник с переменной во времени интенсивностью

q = i(t)AU.

э

Будем искать зависимость температуры 6 центре пятна от времени. Расчет проводится по методу, согласно которому действие непре­рывного источника заменяется суммой действий мгновенных точечных тепловых источников. Основная формула этого метода имеет вид

Рис. 6.3. К расчету нагрева электрода при
неподвижном пятне дуги

Формула (6.2) дает зависимость температуры в центре электрод­ного пятна от времени, свойств материала электрода (X, с, р), плотности тока, эффективного приэлектродного падения напряжения и эффективного значения силы тока. По этой формуле можно оценить допустимый с точки зрения нагрева электрода фазовый сдвиг магнит­ного поля относительно тока дуги. Так как фазовый сдвиг =

где - временной сдвиг между нулевыми значениями тока и магнит­ного поля, то, задавая допустимое повышение температуры поверх­ности электрода в центре пятна ДГ, можно определить допустимый фазовый сдвиг в предположении, что в течение времени / элект­

родное пятно неподвижно:

На рис. 6.4 показана зависимость допустимого фазового сдвига от тока дуги при разных значениях задаваемого повышения температуры и

Рис. 6.4. Зависимость фазового сдвига от силы тока при различных зна­чениях плотности тока и допустимого повышения температуры поверхности

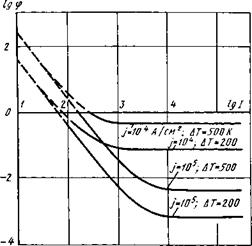плотности тока на медных электродах. При расчете принимали A=

= 10 В. Следует отметить, что выше оси абсцисс расчет дает завы­шенное значение </>, так как здесь замена sin о>/ на <Л уже вносит заметную ошибку в результаты расчетов (на самой оси отличие этих значений составляет 16 %). Кривые рис. 6.4 показывают, что при силе тока порядка 1000 А допустимый фазовый сдвиг составляет от

7г/6 при / = Ю4 А/см2 и ДГ = 500 К до * 2я* 10 3 при / = Ю5 к! си

и ДГ = 200 К. Эти оценки показывают, что с учетом большой степени

неопределенности значений / и AU следует стремиться предельно

э

уменьшать фазовый сдвиг. Формула (6.3) и кривые рис. 6.4 пока­зывают, что зависимость фазового сдвига от силы тока имеет асимп­тотический характер. Это означает, что в рамках принятых допу­щений увеличение силы тока сверх некоторой величины не приво­дит к повышению температуры электрода в центре пятна. Объяс­нение подобной асимптотической зависимости состоит в том, что при /, AU = const рост силы тока приводит к увеличению размера

э

пятна. При этом влияние удаленных от центра мгновенных точечных источнике® на температуру в центре быстро уменьшается с ростом г, что и приводит к указанной асимптотике. Однако необходимо отме­тить, что в действительности условия /, All = const могут не вы-

Э

полниться.

В плазмотронах обычно применяются тонкостенные электроды, для которых расчеты в предположении полубесконечного тела, вообще го­воря, несправедливы. Однако оценки показывают, что при реальных толщинах стенки (2...3 мм) и достаточно малых временных интервалах конечная толщина стенки практически не влияет на результаты при­веденного выше расчета.