В межэлектродном зазоре плазмотрона с магнитной стабилизацией дуга находится в непрерывном сложном пространственном движении под действием электромагнитных и газодинамических сил.

Для расчета электромагнитных сил, действующих на дугу, проведем расчет всех составляющих магнитного поля в межэлектродном зазоре. Осевую Нх и радиальную Н составляющие напряженности магнитного

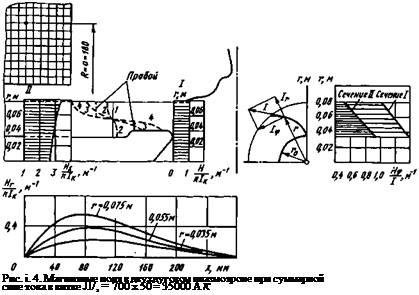
поля можно определить согласно [9], заменяя катушку системой не­скольких витков. Для наших целей можно заменить катушку одним витком с суммарным током всех витков и этот виток расположить в среднем сечении катушки. Рассчитанные магнитные поля для двух­дугового плазмотрона приведены на рис. 1.4. Радиальная состав­ляющая существенно увеличивается вдоль радиуса от поверхности внутреннего электрода до поверхности наружного электрода. На оси симметрии между катушками, а также под каждой катушкой радиальная составляющая магнитного поля отсутствует. Осевая составляющая магнитного поля почти не изменяется по радиусу.

В межэлектродном зазоре возникает также окружная составляющая магнитного поля Н от тока, походящего по электродам к опорным

пятнам дуги. Внутренний и внешний электроды представляют собой цилиндры с толщиной стенки существенно меньше радиуса. Распре­деление тока в таком проводнике аналогично распределению тока в пластине, ширина которой равна периметру электрода. Для упрощения
вычислений цилиндрические электроды были заменены плоскими и на­пряженность магнитного поля в зазоре между пластинами определялась по простой форме, полученной О. Б. Броном. Суммарные напряженности

магнитных полей Н в выходном сечении внутреннего электрода и под 9

катушкой приведены на рис. 1.4.

Рассмотрим электромагнитные силы, действующие на элемент дуги, произвольно расположенный в межэлектродном пространстве (в ци­линдрической системе координат):

Так как эти силы действуют на элемент дуги по всем направ­лениям, то исследование формы дуги становится затруднительным. Для выяснения основных закономерностей перемещения дуги в межэлект­родном пространстве рассмотрим вначале движение и форму дуги при действии на нее только основной осевой составляющей магнитного поля Н.

X

Рис. 1.5. Схема движения электрической

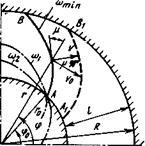дуги под действием магнитного поля лапря -

женностью Н при Н = Н * О Xу Г ф

Схема движения дуги приведена на рис. 1.5. Из положения АВ дуга за время dt перемещается в новое положение с

постоянной угловой скоростью со. Каждый элемент дуги движется по прямой линии, перпендикулярной направлению этого элемента. Можно записать связь между скоростью движения дуги и угловой скоростью:

V = СОГ COS /і.

Форму кривой АВ будем искать в предположении, что форма по­перечного сечения и поперечный размер по длине дуги не меняются. Тогда из равенства электромагнитной силы аэродинамической силе сопротивления следует, что скорость каждого элемента дуги будет зависеть от напряженности магнитного поля в рассматриваемой точке:

Полученное решение дает семейство спиралей, которые могут пе­ремещаться с угловыми скоростями от

Из всех возможных спиралей устойчивой будет спираль (дуга) ми­нимальной длины, определяемая выражениями (1.3) и (1.4). Это соображение основывается на том, что все другие формы дуги будут в процессе горения переходить в спираль, определяемую формулами

(1.3) и (1.4), так как они имеют у поверхности внутреннего элект­рода радиальную составляющую скорости. Отрыв дуги от внутреннего электрода благодаря этой составляющей должен неизбежно привести к появлению элемента дуги, перпендикулярного внутреннему электроду, что и послужит началом перехода к дуге минимальной длины.

Спираль, определяемая выражениями (1.3) и (1.4), быстро меняет свой угол к радиус-вектору: например, при R = 2rQ угол ц = яг/З.

Длина дуги при этом в 1,5 раза больше межэлектродного расстояния.

Рассмотрим, какие движения будут совершать элементы дуги и ка­кую форму будет приобретать дуга под действием всей системы электромагнитных и аэродинамических сил, если начальной формой дуги была спираль, определяемая выражениями (1.3) и (1.4). В на­чальный момент дуга располагается в одной плоскости х = const, поэтому / * 0 и систему электромагнитных сил можно запи­

сать в виде

Движение дуги в плоскости под действием сил Fr и F было рас­смотрено ранее, дуга полученной формы описывается выражением

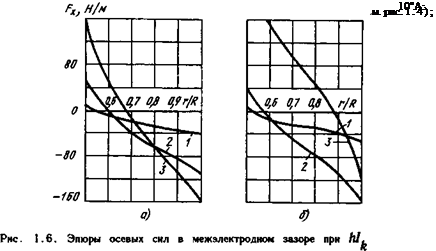
1.4. Эпюры силы F, действующей на дугу такой формы, приведены на рис. 1.6.

Кроме электромагнитных сил на электрическую дугу в направлении оси х действует аэродинамическая сила, которую можно оценить по выражению

(1.6)

Для проведенных авторами опытов средняя скорость движения воз­духа в межэлектродном зазоре составляла величину порядка 1 м/с, а

з

плотность - около 10 кг/м. Характерный размер проводящего канала дуги можно оценить по формуле (3.5). Этот размер при силе тока 5 кА равен приблизительно 1,5 см. Если считать поле скоростей равномерным и принять С = 1, то сила, действующая на элемент дуги единичной длины, Fq = 0,1 Н/м. Сравнение значений аэродинамической
и электромагнитных сил (см. рис. 1.6) показывает, что аэродина­мической силой можно пренебречь. Однако результаты экспериментов, которые приводятся ниже, указывают, что поле осевых скоростей существенно неравномерно и аэродинамическая сила оказывает большое влияние на движение дуги и на место ее горения.

Осевые электромагнитные и аэродинамические силы вытягивают дугу вдоль электрода. Графики суммарной осевой силы, приведенные на рис. 1.6, показывают, что вблизи поверхности внутреннего электрода электромагнитная и аэродинамическая силы всегда действуют в по­ложительном направлении, т. е. к торцу внутреннего электрода. Это вызвано тем, что на поверхности внутреннего электрода / = 0 и

радиальная составляющая магнитного поля не оказывает влияния на движение дуги. У поверхности наружного электрода, наоборот, сум­марная сила Fх всегда направлена в обратную сторону, т. е. в сто­рону катушки. Действующие таким образом силы вытягивают дугу вдоль оси х, и она приобретает ({'фмы» схематически показанные на рис. 1.4. Приэлектродные пятна должны двигаться по спиралям. На поверхности внутреннего электрода эта спираль направлена к торцу электрода, а на поверхности наружного электрода - в обратную сто­рону, под катушку. Если бы электрическая дуга зажглась по другую сторону катушки, то электромагнитная сила изменила бы знак из-за изменения направления радиальной составляющей магнитного поля

Таким образом, катушка оказывает стабилизирующее действие на место горения части дуги, расположенной у наружного электрода, стремясь удержать ее в плоскости симметрии.

Вблизи внутреннего электрода ни одна из рассмотренных сил не удерживает дугу, и она может беспрепятственно вытягиваться потоком и выходить на торец внутреннего электрода. Горение дуги в этой зоне нежелательно, так как здесь направление магнитных силовых линий совпадает с направлением тока, электромагнитная сила на дугу не действует, дуга останавливается и вызывает быстрое разрушение электрода.

Процесс вытягивания дуги вдоль поверхностей электродов огра­ничен вследствие пробоев от дуги к стенкам электродов (механизм шунтирования, см. разд. 1.2). Эти пробои происходят между дугой и поверхностями обоих электродов (см. рис. 1.4). После каждого про­боя образуется новый канал, участок которого вблизи поверхности внутреннего электрода сносится к торцу, а участок вблизи поверх­ности наружного электрода - под катушку до момента нового пробоя. Таким образом, на поверхностях внутреннего и внешнего электродов существуют области значительной протяженности, на которых элект­рическая дуга оставляет следы в виде спиралей.

Для плазмотрона данной схемы пробой от дуги к внутреннему элек­троду происходит по относительно холодному газу, а к внешнему - по газу, нагретому дугой в предыдущих циклах. Поэтому положение об­ласти горения дуги в основном определяется условиями пробоя к по­верхности внутреннего электрода. Напряжение пробоя пропорционально плотности газа. Плотность увеличивается с ростом скорости холод­ного газа v^y так как газ не успевает прогреться, а также с ростом

давления. Поэтому при увеличении давления и скорости газа область горения электрической дуги должна смещаться к торцу внутреннего электрода, что и наблюдается на практике. Кроме того, с ростом плотности газа и его скорости увеличивается аэродинамическая сила, действующая в ту же сторону.

Поведение электрической дуги исследовалось экспериментально в плазмотроне, схема которого показана на рис. 1.3, а магнитные по­ля - на рис. 1.4. Обе электромагнитные катушки включены таким об­разом, что создаваемое ими поле направлено вдоль оси х в одну сторону. Каждая катушка имеет 700 витков. Сила тока в катушках изменялась в пределах 50...300 А. Ток подводился к торцам элек­тродов. При работе на одной дуге токопроводы подключались только со стороны работающей дуги. Обнаружено, что следы дуги в виде спиралей покрывают значительную часть поверхности внутреннего электрода длиной L от торца. Если учесть направление вращения дуги под действием осевого магнитного поля, то можно видеть, что спи­ральные следы на внутреннем электроде начинаются на некотором расстоянии от его торца и заканчиваются вблизи торца или на самом торце. На поверхности внешнего электрода следы дуги начинаются вблизи торца внутреннего электрода и заканчиваются под катушкой.

Такая картина следов дуги полностью соответствует рассмот­ренной выше картине движения дуги в межэлектродном пространстве.

Чтобы проверить влияние скорости обдува дуги на область ее

горения, изменяли расход воздуха G, подаваемого в плазмотрон со

стороны горящей дуги. Часть холодного воздуха подавалась с другой стороны плазмотрона и не проходила через зону горения. Общий рас­ход при этом оставался постоянным и равным 90 г/с, слабо изме-

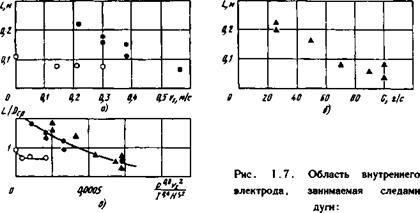
а) при изменении скорости; б) при изменении расхода; в) при изме­нении параметра П; А, • — включены основные соленоиды; о — вклю­ чены дополнительные соленоиды

нялось и давление. Область горения дуги характеризуется протяжен­ностью поверхности внутреннего электрода от плоскости торца до сечения на расстоянии L от него, занятой следами дуги. На рис. 1.7, а приве - дена зависимость длины L от скорости обдува

X О ъ) X

иX

плотность холодного воздуха). Полученная зависимость показывает существенное влияние скорости на положение области горения дуги. При большой скорости дуга горит только на головке электрода. При уменьшении скорости область на внутреннем электроде, занимаемая следами дуги, расширяется, и при = 0,22 м/с дуга практически

горит под катушкой. На внешнем электроде следы дуги всегда зани­мают область ближе к плоскости симметрии катушки, поэтому на внешнем электроде дуга горела под катушкой уже при скорости =

- 0,3 м/с.

Для проверки влияния давления на положение области горения дуги изменялся расход воздуха через плазмотрон. Весь воздух про­ходил через межэлектродное пространство, где горела дуга. Ско­рость при этом практически не изменялась. Результаты экспе­
риментов приведены на рис. 1.7, б. Уменьшение давления (расхода) приводит к заметному перемещению области горения дуги в сторону

катушки.

Связь расстояния L со скоростью и давлением (расходом) можно представить в виде единой зависимости от безразмерного параметра

Здесь d - поперечный размер электрической дуги. Как будет

Подставляя это выражение вместо d, получим параметр

давления. Параметры и зависят от температуры в дуговом ка­нале, которая для дуги, движущейся под действием магнитного поля,

меняется незначительно. Поэтому будем использовать удобный раз-

мерный параметр П = ————- , в котором размерности всех ве­личин выражены в системе СИ. Зависимость L от этого параметра приведена на рис. 1.7, в. Следует подчеркнуть, что параметр П характеризует не только аэродинамическую силу, но и определяет условия пробоя от дуги к внутреннему электроду. Полученные зна­чения этого параметра можно использовать для ориентировочного расчета.

Вид параметра П показывает, что положение дуги в значительной мере определяется величиной магнитного поля и слабо зависит от силы тока дуги. Действительно, изменение силы тока в диапазоне 2000...6000 А привело к изменению параметра П всего в 1,5 раза и практически не повлияло на расположение области горения дуги.

Из приведенных выше результатов видно, что положение области горения дуги в значительной степени зависит от режима работы плазмотрона, что приводит к ограничению диапазона допустимых ре­жимов. При малых расходах и скоростях горячий газ попадает на неохлаждаемые детали за катушкой, что вызывает, в частности,

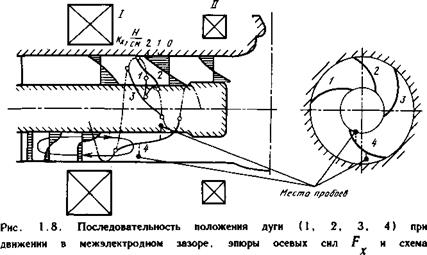
движения нагреваемого газа: I — основной соленоид; П — дополнительный соленоид

большой унос изолятора. Так как режимы с малыми расходами являются режимами максимальных температур, то необходимы эффективные меры по управлению положением области горения дуги. При больших рас­ходах электрическая дуга выносится на торец внутреннего электрода и его ресурс резко падает. Киносъемка показала, что при выходе на торец внутреннего электрода ярко светящееся приэлектродное пятно дуги стоит на одном месте в течение относительно большого времени Ш * 0,005 с), что приводит к значительной эрозии электрода.

Как следует из приведенного выше анализа, управлять положением области горения дуги в коаксиальном плазмотроне можно путем из­менения конфигурации и напряженности магнитного поля. Для этого можно менять форму и место расположения магнитной катушки. Чтобы получить возможность работать на плазмотроне при малых расходах воздуха, основную магнитную катушку выключали, а магнитное поле создавали четырьмя витками, расположенными, как показано на рис. 1.8, вблизи торца внутреннего электрода. Витки включали по­следовательно с электрической дугой. Электродинамическая сила

F^ смещающая дугу под катушку, удерживала ее вблизи торца

электрода. Полученные границы области на поверхности внутреннего электрода, занятой следами дуги, показаны на рис. 1.7. Видно, что дуга сместилась в район минимума радиальной составляющей магнит-

ного поля дополнительного соленоида. Даже при уменьшении расхода через дугу до нуля = 0) она горела вблизи торца внутреннего

электрода. Таким образом, изменение магнитного поля позволило управлять положением области горения дуги, расширить диапазон получаемых параметров и реализовать режим с высокими температурами (до Т0 = 6000 К).

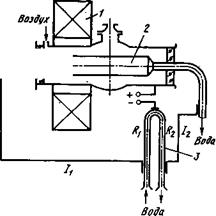
Вынос дуги на торец электрода и его эрозия являются ограни­чением, не позволяющим работать при больших расходах. Имеется ряд работ, посвященных поискам путей защиты торца внутреннего элект­рода от разрушения. Однако в настоящее время эту проблему нельзя считать полностью решенной. Авторы испытали плазмотрон с коак­сиальными электродами, у которого внутренний электрод сделан сквозным, т. е. лишен торца (рис. 1.9). Испытания проводились при силе тока 3 кА, напряженность магнитного поля катушки составляла 1000 А/см. Электроды фактически не разрушались.

На плазмотроне, показанном на рис. 1.9, было изучено влияние магнитного поля токопроводов Н на положение области горения дуги.

При подводе тока со стороны подачи воздуха следы на внутреннем электроде занимали область, смещенную от оси симметрии катушки на расстояние 80... 120 мм. При симметричном подводе тока заметного смещения этой области не произошло. При подводе тока навстречу холодному воздуху область следов заметно, примерно на 20...30 мм, сдвинулась к оси симметрии катушки, однако дуга горела еще далеко внизу по потоку от оси симметрии катушки.

Такой результат экспериментов противоречит оценкам аэроди­намической силы, сделанным по средним параметрам, и свидетель­ствует о том, что следует учитывать неравномерность поля скоростей и существенное увеличение скорости у поверхности внутреннего электрода. Значительная неравномерность скоростей возникает из-за появления циркуляции горячего воздуха (см. рис. 1.8), вызванной тем, что дута при своем основном, вращательном движении создает неуравновешенный градиент давления в плоскости вращения, направ­ленный от внутреннего электрода к внешнему. Наличие такой цирку­ляции горячего газа подтверждается температурными измерениями А. С. Шаболтаса. Весь холодный воздух проходит у поверхности внут­реннего электрода и занимает малое сечение, поэтому скорость его значительно превышает среднемассовую.