Продольно-колеблющийся стержень представляет собой простейшую систему с распределенными постоянными. Предпо­лагается, что поперечные размеры стерж­ня много меньше длины волны, поэтому расхождение отсутствует и волны можно считать плоскими. В этом случае ослабле-

6)

ние волны с расстоянием определяется только коэффициентом затухания 8.

Собственные частоты однородного, свободного на концах стержня длиной I определяются выражением /п=нс/(2/), где с - скорость распространения про­дольной волны в тонком стержне; п - це­лое число (и = 1, 2, 3,..., п).

Собственные частоты рассматривае­мого стержня - кратные числа. Низшая частота f] называется основной, остальные - гармониками. Собственные частоты сво­бодного стержня имеют место, если его длина соответствует целому числу полу­волн: / = rikl 2.

При колебаниях на собственных час­тотах в системе устанавливается стоячая волна, обусловленная интерференцией падающей и отраженной от торца стержня волн (см. разд. 1.1.1). Фаза стоячей волны для каждого сечения постоянна, меняется только ее амплитуда. Сечения стержня, соответствующие максимумам смещения и, колебательной скорости v и силы F, на­зывают пучностями, соответствующие минимумам - узлами колебаний. Так как амплитуды смещения U и колебательной скорости V связаны соотношением V = со U, узлы и пучности смещения и ко­лебательной скорости совпадают.

Для основной частоты узлы силы и пучности смещения находятся на концах стержня, узел скорости и пучность силы - на его середине (рис. 1.69, а). Для второй гармоники характерны три пучности ко­лебательной скорости и два узла силы (рис. 1.69, б). Для п-й гармоники рассмат­риваемого стержня число пучностей сме­

щения п + 1, пучностей силы - п.

Параметрами, необходимыми для анализа колебаний стержней, служат так­же волновое сопротивление и постоянная распространения.

Волновым сопротивлением W стерж­ня называют отношение силы F к колеба­тельной скорости v в бегущей волне:

а значит, и волновое сопротивление среды рс - также комплексная величина. При­ближенное ее значение [312]

рс = р0с0(1 - j'8/к),

где РоСо - волновое сопротивление среды без потерь.

Для материалов с относительно не­большими потерями мнимые составляю­щие волнового сопротивления пренебре­жимо малы и параметры рс и W допусти­мо считать действительными величинами.

В табл. 1.11 приведены формулы для входного механического импеданса ZBX продольно-колеблющегося стержня с раз­личными нагрузками на конце.

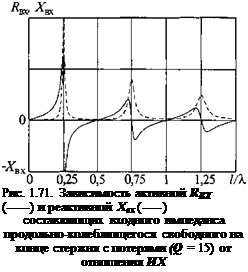
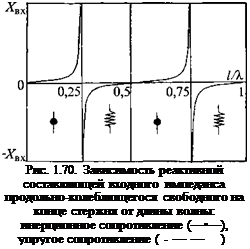
Для свободного на конце (Z = 0) стержня без потерь входной импеданс чисто реактивный: ZBX = jXBK. Зависимость Хвх от отношения ИХ имеет вид тангенсои­ды (рис. 1.70). При ИХ = п/2 (п = 1,2, 3, ...,«) Хвх = 0. При ИХ = (2п - 1)/4 импеданс Хвх меняет знак, переходя через со. Для стерж­ня с потерями и свободным концом (Z = 0)

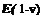
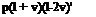
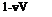
зависимости Хвх и RBX от отношения ИХ показаны на рис. 1.71, для того же стерж­ня с жестко закрепленным концом (Z = со) - на рис. 1.72.

Частоты, соответствующие миниму­мам |ZBX|, называют резонансными, часто­ты, соответствующие максимумам |ZBX|, - антирезонансными. При резонансах и ан­тирезонансах входные импедансы наносят чисто активный характер (ZBX = RBX). При нагрузке на комплексное сопротивление резонансные и антирезонансные частоты смещаются.

Собственные частоты однородного стержня без потерь, один конец которого свободен, другой нагружен механическим импедансом Z = R + jX, при общей доб­ротности системы Q > (5 ... 10) определя­ются выражением

'-ЗгЧ-#)- ,Ы6)

где I - длина стержня; W = pcoS - его вол­новое сопротивление, с0 - ско­рость звука для тонкого стержня.

Формула (1.46) определяет резонанс­ные частоты системы, на которых вход­ной импеданс стержня чисто активный, а его значение минимально. Влияние на­грузки определяется параметром (-X/W). Инерционная нагрузка снижает собствен­ные частоты, упругая увеличивает. При реактивной нагрузке собственные частоты перестают быть кратными основной час­тоте и называются уже не гармониками, а обертонами.

Скорость распространения про­дольных волн в стержне зависит от от­ношения его поперечного размера d к длине волны X. Для стержней с d/X « 1

Со = у[Щр, как в табл. 1.2. Для неограничен­ной среды (d/X » 1) скорость с/ = При промежуточных
значениях отношения d/X зависимость скорости с от этого параметра имеет сложный характер. Это явление называет­ся геометрической дисперсией скорости.

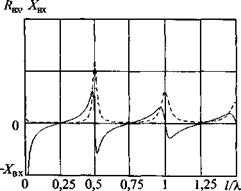
На рис. 1.73 показана зависимость отношения с/с/ от параметра d/2X для круглого стержня из материала с v = 0,33. Эти данные можно использовать и при v = (0,25 ... 0,35) [312]. В области 0,8 < d/2X <1,1 распространения упругих волн практически не наблюдается, так как энергия не может переноситься волнами этого типа при такой скорости. Из графика следует, что при условии d/2X > (2,5 ... 2,8) стержень уже можно рассматривать как неограниченную среду.

Скорость продольной волны в ци­линдрическом стержне диаметром d мож­но вычислить по приближенной формуле Похгаммера [312] f d__ V

2Х,

При d/2X <0,15 формула (1.47) дает результаты, мало отличающиеся от полу­ченных по значительно более сложной точной формуле: при 0,15 < d/2X < 0,2 и 0,5 < d/2X < 0,7 ошибка не превышает 3 ... 4 %. В области 0,2 < d/2X < 0,5 фор­мула дает завышенные результаты, пог­решность не превосходит 15 %. При d/2X > 0,7 формулой пользоваться нельзя.

Для стержня квадратного сечения со стороной h можно использовать выраже­ния для круглого стержня, приняв

d/h= 1,28.