Ближняя и дальняя зоны. Здесь рассматривается не только преобразова­тель, излучающий непосредственно в ОК, но и любой преобразователь, излучающий в однородную среду, например в жид­кость. Поле в среде описывается сущест­венно разными закономерностями на близком и далеком расстояниях от преоб­разователя. Это различие особенно четко выражено для круглого преобразователя. В непосредственной близости от него УЗ распространяется в виде параллельного пучка лучей (прожекторная зона), но чуть дальше картина резко изменяется. Энергия по-прежнему остается в пределах нерасходящегося пучка, но появляются

Рнс. 1.45. Поле излучения на оси круглой пьезопластины (а) и схематическое изображение поля (б): (----- ) - непрерывное излучение; (---- ) - излучается колоколообразный импульс

с показателем длительности у = 0,25;

максимумы и минимумы амплитуды. Вся эта область называется ближней зоной, ближним полем или зоной Френеля.

В дальней зоне {дальнем поле, зоне Фраунгофера) формируется расходящийся пучок лучей. Излучается как бы сфериче­ская волна, но распространяющаяся не равномерно во все стороны от источника, а в пределах конуса - основного лепестка. Максимум амплитуды соответствует оси преобразователя {акустическая ось или центральный луч). С увеличением угла между направлением какого-либо луча и осью амплитуда уменьшается, появляются боковые лепестки. Зависимость амплиту­ды излучения от направления луча назы­вается диаграммой направленности.

При некотором угле {угле раскры­тия) амплитуда излучения равна нулю для непрерывного излучения, а для импульс­ного наблюдается минимум). Угол рас­крытия определяет основной лепесток. За его пределами обычно появляются боко­вые лепестки, которые являются источни­ками помех.

В дальней зоне амплитуда плавно уменьшается с увеличением расстояния от преобразователя. В ближней зоне ампли­туда изменяется от положения в простран­стве сложным образом.

Граница между ближней и дальней зонами приближенно определяется фор­мулой:

N = S/{nX) = a2/x, (1.26)

где N - расстояние вдоль оси х; совпа­дающей с акустической осью преобразо­вателя', S - площадь пьезоэлемента; X - длина волны. Последняя часть формулы соответствует круглому пьезоэлементу радиусом а. Первая часть приближенно пригодна также для квадратного пьезо­элемента.

При конструировании преобразова­теля обычно стремятся уменьшить осцил­ляции амплитуды в ближней зоне и повы­сить направленность в дальней зоне, т. е. уменьшить угол раскрытия и боковые ле­пестки. Исследования показывают, что решить одновременно все задачи не уда­ется. Некоторые практические условия контроля требуют, наоборот применения преобразователя с широкой диаграммой направленности.

Дискообразный преобразователь.

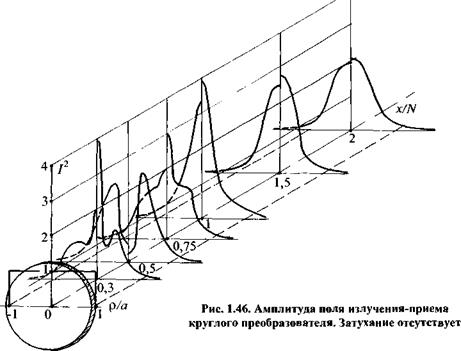
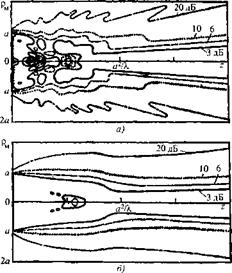
Ближняя и дальняя зоны хорошо выраже­ны в поле преобразователя с дискообраз­ной (круглой) пьезопластиной, как отме­чалось ранее. На рис. 1.45, б схематически изображено поле излучения в ближней и дальней зонах, а на рис. 1.45, а - измене­ние амплитуды излучения на оси х, совпа­дающей с геометрической осью диска. На рис. 1.46 показан общий вид поля излуче­ния-приема круглого преобразователя в безразмерных координатах xIN и р/а2 (р - расстояние точки В от оси х).

Как отмечалось, в ближней зоне ам­плитуда очень резко изменяется в зависи­мости от положения точки в пространстве, а в дальней зоне она плавно уменьшается с увеличением расстояния от преобразова­теля. Так же будет изменяться амплитуда сигнала, отраженного от небольшого де­фекта. Чем крупнее дефект, тем больше сглаживаются изменения амплитуды эхо - сигнала в ближней зоне. Например, ам-

плитуда отражения от перпендикулярной к оси плоскости в ближней зоне сохраня­ется постоянной с точностью в 20 %. Это соответствует очень слабому расхожде­нию энергии излучения в ближней зоне.

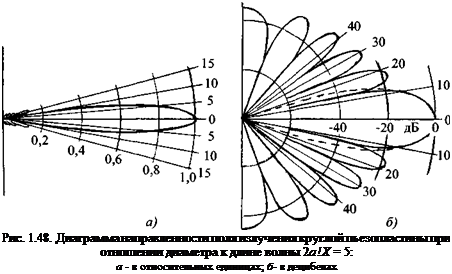
При излучении коротких импульсов сглаживаются максимумы и минимумы. Это хорошо видно для поля излучения - приема на рис. 1.46. Кривые справа соот­ветствуют длинному импульсу с показате­лем длительности v = 0,05, а слева - ко­роткому с v = 0,17. На рис. 1.47, а и 6 по­казаны линии равного ослабления ампли­туды излучения соответственно для v = 0,014 и v = 0,17.

Поле излучения вдоль оси х круглого преобразователя (см. рис. 1.45, а) без уче­та импульсного характера излучения опи­сывается формулой

Р = Р01е-&с ;

где Р - акустическое давление в точке В поля; Р0 - давление на поверхности излу-

Рис. 1.47. Поле излучения круглой пьезопластины в виде линий равного ослабления амплитуды давления для колоколообразных высокочастотных импульсов

чателя; 8 - коэффициент затухания (в даль - дальнейших формулах затухание не учи­тывается); А: - волновое число.

Приближенная часть формулы пред­полагает выполнение условия а « х. Наи­более удаленный от излучателя максимум определяет границу ближней зоны. Он соответствует равенству п/2 аргумента синуса. Из этого следует

N2 +а2 - N = Х/2;

N = а2Д-А./4. (1.28)

Если радиус а круглого преобразова­теля (точнее, его пьезопластины) значи­тельно больше длины волны (что обычно выполняется), то N вычисляется с доста­точной точностью по формуле (1.26).

Возникновение максимумов и мини­мумов акустического поля в ближней зоне преобразователя объясняется интерферен­цией сигналов, приходящих от различных точек преобразователя и проходящих путь разной длины до точки В. Пьезопластину можно представить состоящей из большо­го количества маленьких излучателей. Расстояния от разных излучателей до не­которой точки В в ближней зоне могут сильно различаться. Соответственно, бу­
дут разными фазы приходящих сигналов. При их совпадении амплитуда увеличива­ется, если фазы противоположны (т. е. от одних излучателей поступают волны, тре­бующие растяжения объема около точки В, а от других - требующие его сжатия), амплитуда уменьшается [319].

Экранируя зоны пьезопластины, от которых сигнал приходит в противофазе, или сдвигая фазу на п/2 (путем переклю­чения электродов), добиваются сущест­венного увеличения амплитуды в точке В. На этом основана фазовая фокусировка.

Оценивать дефекты, находящиеся в ближней зоне, по амплитудам отраженных сигналов трудно: можно ошибиться в оп­ределении местоположения и числа де­фектов. Например, на расстоянии х = N12 от преобразователя (в середине ближней зоны, см. рис. 1.46) поле имеет минимум на оси ПЭП, а в стороне - максимум. При поиске и оценке дефектов по максимумам эхосигналов дефектоскопист, найдя в дей­ствительности один дефект, решит, что найдено два дефекта, расположенных по сторонам от истинного положения дефекта.

Исходя из сказанного, в России вы­пускают преобразователи с небольшой длиной ближней зоны. Например, прямой преобразователь на частоту /= 2,5 МГц с
диаметром 2а = 12 мм имеет длину ближ­ней зоны в стали N= a2 flс = 62 • 2,5/5,9 « «15 мм. В других странах считают вполне возможным вести контроль в ближней зоне. Считают, что дефектоскопист дол­жен знать особенности ближней зоны, учитывать их. Например, широко приме­няют преобразователь с/= 4 МГц и 2а = = 24 мм, для которого /V» 100 мм.

В дальней зоне появление максиму­мов и минимумов акустического поля под влиянием разности фаз приходящих волн происходит только, когда точка В нахо­дится в стороне от оси преобразователя. Основная часть поля имеет вид расходя­щихся конусом лучей из центра преобра­зователя. Амплитуда поля излучения вдоль оси х уменьшается по закону S/{hc).

Для некоторого расстояния х = г примем амплитуду излучения на оси рав­ной 1. Для луча под углом 0 к оси ампли­туда будет меньше, она в этом случае описывается некоторой функцией Ф(0) - диаграммой направленности. Таким обра­зом, поле излучения выражается форму­лами

Р = Ртф(0); Pm=P0S/(Xr). (1.29)

На рис. 1.48 дан пример диаграммы направленности в относительных едини­цах и децибелах. Сравнение графиков де­монстрирует различие масштабов в пред­ставлении результатов: в относительных единицах лепестки едва заметны, а в де­цибелах хорошо видна их структура, но они кажутся преувеличенно большими.

Показанный на рисунке вид лепестки имеют в сечении пространственного аку­стического поля плоскостью рисунка. В действительности каждый лепесток ог­раничивается двумя коническими поверх­ностями с большим и меньшим углами при вершине.

Угол 0 = 0о ограничивает основной лепесток диаграммы направленности. При нем Ф обращается в нуль. В основном ле­пестке сосредоточено ~80 % энергии поля. Существующие за его пределами боковые лепестки являются источниками помех. Наибольший их уровень дает первый бо­ковой лепесток.

Угол 0о называют углом раскрытия диаграммы направленности. Его рассчи­тывают по формуле

sin0o=«A,/a; (1.30)

здесь п - численный коэффициент, равный для круглого преобразователя 0,61. Обыч­но считают, что, когда амплитуда поля излучения-приема уменьшается в 10 раз

(Ф2 = 0,1; Ф = д/ОД), акустическое поле практически отсутствует. Для этого уров­ня угол раскрытия будем обозначать 0Од, для него коэффициент п = 0,45 « 0,5. Для характеристики раскрытия акустического поля на других уровнях вычисляют соот­ветствующие значения коэффициента п.

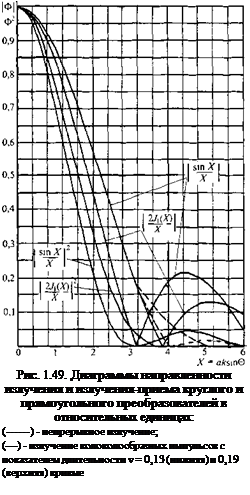
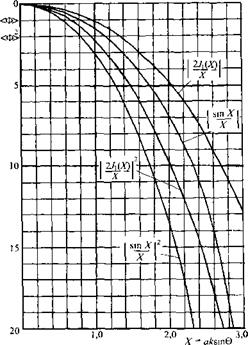
На рис. 1.49 сплошными линиями по­казаны диаграммы направленности полей излучения и излучения-приема круглого преобразователя, которые определяются формулами

ф{х) = их{х)1х;

Ф2(х) = и1{х)/Х2; X = aksi пО,

где J - функция Бесселя первого порядка; к - волновое число в среде. Хорошо видны минимумы и боковые лепестки.

Диаграммы направленности, пока­занные сплошными линиями, соответст­вуют непрерывному излучению или им­пульсам очень большой длительности. Диаграммы направленности для реально применяемых коротких импульсов пред­ставлены штриховыми линиями. Расчет сделан для импульсов колоколообразной формы, показатели их длительности равны v = 0,13 для нижней кривой и 0,19 для верхней. При импульсном излучении нули отсутствуют, форма кривых в нижней час­ти меняется. По этой причине ширину

диаграммы направленности лучше оцени­вать на уровне л/0Л, где этих изменений практически нет.

В табл. 1.10 приведены более полные данные о дальней зоне преобразователей с пьезопластинами различной формы. Пер­вая строка соответствует дискообразному преобразователю. Ввиду того что диа­граммы направленности при излучении и излучении-приеме для круглого и прямо­угольного преобразователей часто исполь­зуют в расчетах, они приведены на рис. 1.49 и 1.50 в относительных единицах и децибелах в функции от безразмерного параметра X.

Поле излучения круглого преобразо­вателя в пределах основного лепестка можно описать аналитически приближен­ными формулами [350]

ф==е-о,142Х2 . ф = 1,32-0’5*2 ; (1.31) здесь как и ранее, X = ак sin 0. Формулы особенно хорошо совпадают с кривыми для излучения коротких импульсов.

При больших значениях углов 0 вво­дят множитель х(9)> учитывающий транс­формацию продольных волн в поперечные при излучении [120]:

_________ (2/С2 sm2 е - fc,2 j2___________

(2А2 sin2 0 — Агг2 j2 + 4kf sin2 0cos - k] sm2 0 где к/ и к, - волновые числа для продоль­ных и поперечных волн.

Рис. 1.50. Диаграммы направленности излучения и излучения-приема круглого и прямоугольного преобразователей в децибелах

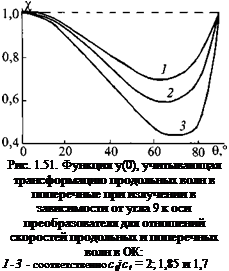График функции у(9) для различных отношений скоростей продольных и попе­речных волн с, /с, показан на рис. 1.51. В результате вместо (1.29) записывают

Р«РтФ(0)х(0), (1-32)

где Ф - определенная выше диаграмма направленности. При углах 0 < 20° функ­ция х(0) ~ 1 и справедливы формулы (1.29).

Ранее были даны значения длины ближней зоны для двух типичных преоб­разователей. Приведем для них же значе­ния углов раскрытия. Для преобразовате­ля, часто применяемого в России,

Фо j = arcsin(o,45c/ fa) =

= arcsin(0,45-5,9/2,5-6) = 11,3°,

а для часто используемого в других стра­нах, <р0,1 = 3,5°. Расхождение лучей гораз­до меньше, что, как правило, удобно для контроля.

Кольцеобразный преобразователь.

В таком преобразователе пьезоэлемент имеет форму кольца с наружным и внут­ренним диаметрами 2а„ и 2ав. Иногда пье­зоэлемент делают дискообразным, а фор­му кольца придают электродам. Амплиту­да поля излучения на оси кольцеобразного преобразователя приближенно определя­ется формулой

Р = Р07;

Формула для протяженности ближ­ней зоны

пХ X

Поле излучения в дальней зоне

I и _ я -2 2У, (fta„ sin 9) 2 27, (кав sin б)

Хг н (кан sin 0) в (fajB sin 0)

В табл. 1.10 представлена формула для предельного случая бесконечно тонко­го кольца. Угол раскрытия 0, при котором
использованная в ней функция Бесселя нулевого порядка Jo обращается в нуль, рассчитывают по формуле

sin0o = 0,39Х/а.

Уменьшение коэффициента п по сравнению с дискообразным преобразова­телем показывает, что кольцеобразный пьезоэлемент имеет более узкую диаграм­му направленности, чем дискообразный. Одновременно с этим увеличились боко­вые лепестки.

Преобразователи с кольцеобразным пьезоэлементом редко применяют в де­фектоскопии, так как уменьшение полез­ной площади излучателя-приемника сни­жает чувствительность.

Прямоугольный преобразователь. Пьезопластину прямоугольной формы применяют в наклонных и РС-преобразо - вателях. Здесь рассмотрено поле такой пластины без акустической задержки.

Согласно EN 12668-2, граница ближней зоны (как положение последнего макси­мума) преобразователя с прямоугольной пластиной определяется следующим спо­собом. Рассчитывают отношение сторон

1.10. Диаграммы направленности пьезопластин различной формы Форма пьезопластины Диаграмма направлен­ ности Ф(Х) Аргумент X Коэффициент п для раскрытия основного лепестка на уровне |Ф|, равном Максимум бокового лепестка 0 0,1 Vw 0,5 Vos Диск, диаметр 2 а ак sin 0 Эллипс, полу­оси ау и az 2JX{X)IX (a2 cos2 ср + +я2 sir? ср)^2 х хк sin 0 0,61 0,55 0,45 0,35 0,26 0,14 Тонкое коль­цо, диаметр 2 а 1 •/<>(*) 1 ак sin 0 0,39 0,35 0,28 0,24 0,18 0,40 Прямоуголь­ник, стороны 2 ауу 2 az sinХу sinA. a^fcsinO^; a^sinOj ху хг 0,50 0,45 0,38 0,30 0,22 0,21

Примечание. Угол ср в формуле таблицы для эллиптического преобразователя определяет плоскость, в которой требуется рассчитать диаграмму направленности. Для плоскостей, проходящих через оси эллипса ср = 0 и 90°, имеем X = аук sin 0,, и

X = azksmbz.

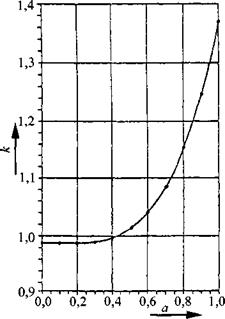
a = axja2, где a2 >at. По нему находят фактор к по рис. 1.52. Тогда протяжен­ность ближней зоны прямоугольного пре­образователя равна N = (ках )/(4л).

Сравнение результата, полученного по этой формуле, с прямым вычислением поля на оси показало, что они совпадают с точностью до 10 %. Например, для квад­ратной пластины положение последнего максимума приближенно определяется формулой

N = S/nX,

что на 7 % меньше, чем по EN 12668-2.

Сравнение с полем круглого преобра­зователя показывает, что в ближней зоне максимумы и минимумы сглажены. До­полнительное их сглаживание наблюдает­ся для импульсного излучения.

Расхождение лучей (диаграмму на­правленности поля излучения прямо­угольного преобразователя) описывает формула табл. 1.10. Из нее следует, что направленность разная в двух взаимно перпендикулярных плоскостях и зависит от волнового размера пластины в каждой плоскости. Диаграмма направленности поля излучения-приема получается возве­дением в квадрат формул табл. 1.10, как показано на рис. 1.49 и 1.50.

Пример 1.11. Сравнить преобразователи с пластинами разной формы с позиций наилучшей направленности полей излучения-приема в стали. Частота / = 2,5 МГц, максимальный размер пла­стины 2а = 20 мм.

Направленность поля излучения-приема оп­ределяет функция Ф2. Найдем углы раскрытия основного лепестка на уровне Ф2 = 0,1 или |ф| = л^0Д по формуле (1.30) и данным табл. 1.10

для круглой, кольцеобразной и прямоугольной пластин:

0'= arcsin[o,45c/(/a)] = arcsin[o,45 -5,92 /(2,5 -10)] = 6,1° ;

9'= arcsin[0,28 5,92/(2,5 10)]= 3,8°;

0'=arcsm[o,38 5,92/(2,5 ю)] = 5,2°.

Строго говоря, максимальным размером прямоугольной пластины является не сторона, а диагональ. Для квадратной пластины с диагона­лью 20 мм [полусторона а = 20/(2>/2)= 7,07 мм] получим

0'=arcsm[o,38 5,92/(2,5-7,07)]= 7,3° .

Таким образом, квадратная пластина обес­печивает наихудшую, а кольцеобразная - наи­лучшую направленность. Но кольцеобразная пла­стина имеет меньшую полезную площадь (а сле­довательно, и меньшую чувствительность), чем круглая такого же диаметра; для нее уровень бо­ковых лепестков в 0,4/0,14 = 2,9 раза выше, по­этому обычно применяют круглые пластины.

Преобразователи с сильно вытянутой пьезопластиной представляют интерес в отношении увеличения полосы изделия (например, листа), контролируемого за один проход. Такие преобразователи на­зывают широкозахватными. Недостаток таких преобразователей заключается в неравномерности чувствительности вдоль большей стороны пластины из-за интер­ференции в ближней зоне. Для выравни­вания чувствительности предложен ряд способов, например ширина пластины в центральной части сужается.

Эффективный размер пьезопластины часто неизвестен. Например, иногда на ее края не наносят электродов и остается неизвестным, какую площадь пьезопла­стины S следует использовать: общую или только площадь, покрытую электродом, поэтому затруднительно использовать простые формулы для расчета протяжен­ности ближней зоны N. Как отмечалось ранее, максимум в ближней зоне часто выражен нечетко, например для прямо - угольугольного преобразователя при им-

Рис. 1.52. Корректирующий фактор к для расчета протяженности ближней зоны прямоугольного преобразователя: а - отношение сторон

пульсном характере излучения.

С учетом этого EN 12668-2 предлагает определять границу ближней зоны преобра­зователя по расхождению лучей в дальней зоне. Например, для преобразователя с пря­моугольной пластиной измеряют угол раскрытия у2. параллельный большей сто­роне. Для акустического поля излучения этот угол соответствует ослаблению ам­плитуды на 3 дБ, а для поля излучения - приема он соответствует ослаблению ам­плитуды на 6 дБ. Предполагается извест­ной центральная частота f0. Тогда эффек­тивное значение стороны a2eff прямо­угольного преобразователя рассчитывает­ся по формуле

a2eff = (0,442с)/(/0 sin[y 2 ]).

Аналогичным образом определяется эффективное значение для другой стороны и, далее, выполняется процедура расчета протяженности ближней зоны, рассмот­ренная выше.