1.1. УПРУГИЕ КОЛЕБАНИЯ И ВОЛНЫ

1.1.1. Основные понятия

Колебание - движение вокруг неко­торого среднего положения, обладающее повторяемостью, например колебание ма­ятника. В акустике обычно рассматривают колебания точки среды относительно по­ложения, в котором точка находилась в покое. Волны - колебательные движения, распространяющиеся в пространстве: ко­лебания одной точки передаются соседней и т. д. В большинстве видов неразрушаю­щего контроля (радиационном, оптиче­ском, тепловом, радиоволновом) исполь­зуются электромагнитные колебания и волны. В отличие от них в акустических видах используются упругие колебания и волны.

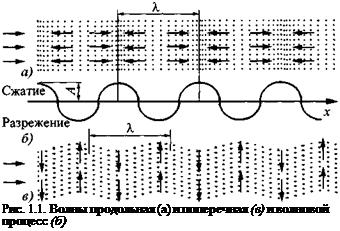
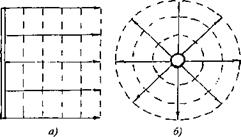
Упругость - свойство точек среды возвращаться к первоначальному состоя­нию после прекращения воздействия си­лы. Жидкие, газообразные и твердые сре­ды восстанавливают свой объем после сжатия или разрежения, но под действием сил инерции точки продолжают двигаться после достижения первоначального со­стояния. В результате сжатие переходит в растяжение, а потом опять в сжатие - воз­никают упругие колебания. Такой процесс распространяется в пространстве и обра­зует упругую волну (рис. 1.1, а, б).

Обычно акустические колебания происходят в области, где механическое напряжение пропорционально деформа­ции для твердого тела или давление про­порционально смещению для жидкости, газа. Это область упругого взаимодейст­вия, ей соответствует линейная акустика. Однако при больших отклонениях от по­ложения равновесия пропорциональность нарушается. Это область нелинейной аку­стики. Неразрушающему акустическому контролю, как правило, соответствует только область линейной акустики. Неко­торые вопросы, связанные с применением нелинейной акустики, будут рассмотрены в разд. 1.5.

Колебательный процесс характеризу­ется двумя основными величинами: часто­той и амплитудой колебаний.

Частота - количество колебаний в секунду (с). Ее обозначают буквой f Одно колебание в секунду - 1 герц (Гц). При УЗ-контроле обычно частоту колебаний измеряют в мегагерцах (МГц) - миллио­нах колебаний в секунду или килогерцах (кГц) - тысячах Гц. В зависимости от час­тоты / упругие колебания и волны назы­вают по-разному (табл. 1.1). При высоко­частотном акустическом контроле обычно применяют колебания частотой 0,5 ... 100 МГц, а при низкочастотном - частотой 0,015 ... 0,1 МГц.

Время одного колебания называют периодом Т. Его измеряют в секундах или микросекундах (мкс):

f = l/T.

Колебания от точки к точке среды передаются с определенной скоростью - скоростью распространения звука с. Рас­стояние, пробегаемое волной за один пе­риод колебаний, называют длиной волны X,

Х = сТ - с//.

Скорость звука во многих металлах ~6000 м/с = 6 мм/мкс. При частоте 6 МГц длина волны равна 1 мм. Волны длиной ~1 мм (точнее, 0,2 ... 10 мм) обычно упот­ребляются при высокочастотном УЗ-кон­троле металлов. Небольшая длина волны по сравнению с размером преобразователя позволяет создать направленно-распро - страняющуюся волну, которую рассмат­ривают как пучок лучей.

Часто применяют понятия "круговая {циклическая, угловая) частота" со = 2 д/

и "волновое число"

к = со/с = 2п/Х.

Амплитуда. Амплитуда колебаний - это наибольшее отклонение от положения равновесия (см. рис. 1.1, б). Упругие коле­бания характеризуют разными физиче­скими величинами. Для жидкостей и газов чаще всего используют следующие вели­чины: смещение и частиц из положения
равновесия, скорость движения частиц {колебательную скорость) и акустическое давление р.

Для твердых тел обычно используют вектор смещения й и тензор акустиче­ских напряжений (см. далее). В дальней­шем для упрощения формул колебания в твердом теле будем, как правило, характе­ризовать их акустическим давлением, что не вполне правомерно, но существенно упрощает математический аппарат. Там, где возникает необходимость, учитывают­ся особенности твердого тела.

1.1. Диапазон частот упругих колебаний Название колебаний и волн Качественное определение Диапазон частот, Гц физический условный Инфразвук Ниже границы слыши­мости человека < 16 ... 25 <20 Звук Диапазон слышимости человека От 16 ... 25 до (15 ... 20)103 20 ... 20 000 Ультразвук Выше границы слы­шимости человека От(15 ... 20)103 до 109 (20 103)... 109 Г иперзвук Длина волны меньше длины свободного про­бега молекул воздуха > 109

Шкала децибелов

/> // 0,01 ІІГ 0,001

500 1000

Отношение амплитуд

Рис. 1.2. Шкалы перевода относительных величии в децибелы. Попарно используют шкалы 1-Г, ІІ-ІГ, III-IW

Будем обозначать амплитудные зна­чения соответствующими большими бук­вами, а в общем случае - буквой А. В УЗ - дефектоскопии обычно применяют коле­бания с амплитудой смещения 10‘" ... 10‘4 мм. Акустическое напряжение, возни­кающее при этом в стали на частоте 2 МГц, достигает 10 ... 108 Па (паскаль).

Энергия акустической (звуковой) - волны это добавочная энергия, обуслов­ленная наличием этой волны. Энергия акустической волны в единице объема среды называется плотностью звуковой энергии. Она состоит из кинетической и потенциальной частей. Для плоской бегу­щей звуковой волны кинетическая и по­тенциальная части энергии равны и плот­ность полной энергии, выраженная через амплитуду давления Р, равна

Е = Р2/(рс2),

где р - плотность среды.

Интенсивность (сила) звука J - сред­няя по времени энергия, переносимая зву­ковой волной через единичную площадку, перпендикулярную к направлению рас­пространения волны, за единицу времени. Для периодической звуковой волны ус­реднение проводится либо за промежуток времени, намного больший по сравнению с периодом, либо за целое число периодов. Для плоской синусоидальной бегущей волны интенсивность, выраженная через амплитуды давления Р и смещения U, равна

J = Р2/(2рс) = 0,5рсш2£/2 .

Интенсивность используемых при контроле волн обычно весьма мала: <10-5 Вт/м2 в месте излучения УЗ. При УЗ - контроле, как правило, регистрируют не интенсивность, а амплитуду волн.

В УЗ-контроле обычно измеряют ос­лабление амплитуды А' относительно ам­плитуды возбужденных в ОК колебаний Aq. Для этого применяют логарифмиче­ские единицы - децибелы (дБ). Выражения в дБ, когда это необходимо подчеркнуть, будем выделять угловыми скобками ( 'j:

{А'/Ао) = 20]^А'/Ао) = 10ф'/А0).

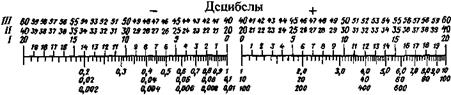
Поскольку А’<А0, децибелы будут отрицательными, однако в УЗ-дефекто - скопии знак принято опускать. На рис. 1.2 приведена шкала перевода отно­сительных единиц в положительные и от­рицательные дБ.

Пример 1.1. Как отношение амплитуд Л’/Л0 = 0,045 выражается в дБ?

Находим деление 0,045 на шкале ІГ (см. рис. 1.2). Против него на шкале II находим: (А/ А0) = 26,9 дБ со знаком но его не указы­ваем.

Если потери невелики, то возбужден­ный колебательный процесс продолжается очень долго. При отсутствии потерь воз­никают непрерывные гармонические коле­бания, т. е. изменяющиеся по синусои­дальному закону. В УЗ-контроле обычно
колебания возбуждают и тут же стараются погасить. В результате наблюдается крат­ковременный волновой процесс - импульс.

Одним из параметров колебаний и волн является их фаза. Она характеризует состояние колебательного процесса в оп­ределенный момент времени. Если коле­бания непрерывные, то фаза колебаний повторяется через каждый период. Для импульсов строгая повторяемость пара­метров колебаний через период отсутству­ет. Говорят, что две непрерывные гармо­нические волны находятся в противофазе, если их фазы отличаются на полпериода. Если на какую-либо точку действуют две такие волны с одинаковыми амплитудами, точка не колеблется, а если фазы этих волн совпадают, амплитуда колебаний увеличивается в 2 раза. Явление сложения волн с учетом их фазы называют интер­ференцией волн.

Волновое уравнение. Здесь приво­дится упрощенное изложение теории вол­нового процесса. Рассматривается распро­странение волны только вдоль одной ко­ординаты х [219].

Как частично отмечалось ранее, уп­ругие колебания в жидкостях и газах ха­рактеризуются одной из следующих вели­чин: изменением давления р или плотно­сти, смещением частиц из положения равновесия и, скоростью колебательного движения (колебательной скоростью) v, потенциалом смещения или колебатель­ной скорости. Все перечисленные величи­ны взаимосвязаны. Следует отличать из­менение давления или плотности, связан­ное с распространением акустических волн, от их статистического (среднего) значения.

В твердых телах акустическое поле имеет гораздо более сложный вид, чем в жидкостях и газах, потому что твердым телам присуща не только упругость объе­ма, как жидкостям и газам, но и упругость формы (сдвиговая упругость). Вместо давления для твердых тел вводят понятие "напряжение", т. е. "сила, отнесенная к единице поверхности".

Различают нормальные (растягиваю­щие или сжимающие) напряжения а хх,

Gyy, а22, касательные или тангенциаль­ные (сдвиговые) напряжения а^, ст^ и

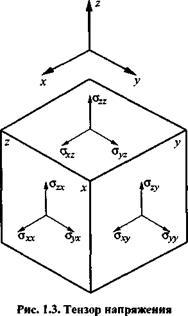
др. Напряженное состояние твердого тела, таким образом, характеризуют тензором третьего ранга о,7 - таблицей из девяти чисел-компонентов. Индексы і и / прини­мают значения осей координат х, у, z. Пер­вый индекс указывает координату, в на­правлении которой действует сила, а вто­рой - площадку (грань элементарного ку­ба), перпендикулярную к направлению указанной в нем координаты, к которой эта сила приложена (рис. 1.3). Тензор этот симметричный: в нем ст,; = ст;,, а значит, шесть независимых величин.

В жидкостях и газах, где не сущест­вует упругости формы, тангенциальные компоненты тензора напряжения отсутст­вуют, а нормальные компоненты равны друг другу и давлению с обратным зна­ком. Давление имеет знак потому что напряжение считают положительным, ко­гда оно растягивающее, а давление отно-

Рис. 1.4. Компоненты тензора деформации

сят к положительным, если оно сжимаю­щее.

Колебания в твердом теле характери­зуются, как отмечалось, изменением на­пряжения, вектора смещения частиц и, и потенциала смещения. Понятием "колеба­тельная скорость" для твердого тела поль­зуются редко. Часто колебания характери­зуют деформацией - изменением взаимно­го расположения ди точек тела. Это изме­нение относят к первоначальному рас­стоянию между точками, в результате чего деформация становится безразмерной ве­личиной. Если точки сдвинулись вдоль отрезка, их соединяющего, то это дефор­мация растяжения-сжатия (рис. 1.4, а), Если точки сдвинулись перпендикулярно к этому отрезку, то это деформация сдвига (рис. 1.4, б). В результате деформацию записывают в виде тензора єг/, аналогич­ного тензору напряжений. В нем гхх = дих/дх -деформация растяжения-сжа­тия вдоль оси х и аналогично для других осей. Чтобы сделать тензор деформаций симметричным, компонент запи­

сывают в форме сх>. = [дих /ду + диу/дх)/2

(рис. 1.4, в) и также для других сдвиговых компонентов деформации. Величина z = zxx+Zyy+ szz означает изменение объ­ема dxdydz элементарного куба. Для жид­костей и газов деформации сдвига отсут­ствуют, а деформации растяжения-сжатия по всем направлениям одинаковы.

В этой главе рассматриваются изо­тропные среды. Изотропия - независи­мость физических свойств среды от на­правления в ней. Среды, в которых свой­ства зависят от направления, называют анизотропными. Более подробно такие среды будут рассмотрены в разд. 7.2.

Пропорциональную зависимость ме­жду напряжениями и деформациями на­зывают законом Гука. В обобщенном виде его записывают в виде [219, 220]

ст,/ = 8,/Ає// + 2рєг/,

где ди= 1, когда г = /, и 5,; = 0, когда і Ф I.

Аир - константы Ламэ. В технике вме­сто последних используют модули нор­мальной упругости Е и сдвига G:

Е = р(ЗА + 2р)/(А + р); G = р.

Важная упругая константа - коэффи­циент Пуассона v, равный отношению сжатия к удлинению растягиваемого стержня:

Л _ Е V 2(л + р) _ 2G

Во всех случаях упругие свойства изотропного твердого тела характеризуют парой независимых упругих констант.

Волновое уравнение для твердого те­ла выводят [219, 220] путем применения второго закона Ньютона к элементарному объему dxdtydz. Разность сил, приложен­ных к противоположным его граням, при­равнивают к произведению массы на ус-

корение. В результате получают для оси х:

д2и

Аналогично можно записать уравне­ния для осей у и z. Здесь t - время.

Подставляя вместо напряжений де­формации по закону Гука, получают урав­нение распространения волн в упругой среде:

Р

(л + ц)—цУ2их =0, дх

„2 0 0 0 п

где V = —- + —- + —-— оператор Лап-

дх2 ду2 dz2

ласа. Это волновое уравнение. Его харак­терная особенность заключается в том, что в него входят с разными знаками вторые производные по времени и координатам от некоторой переменной величины.

Если положить р = 0 и считать сме­щения их - иу —uz =и одинаковыми по

всем направлениям (скаляр), то волновое уравнение для твердого тела переходит в волновое уравнение для жидкости или газа:

d2ujdt2 = c2V2h,

где с = д/Х/р - скорость распространения

акустических волн.

Такие же уравнения справедливы и для других упругих величин: давления, плотности и т. д. Будем обозначать эти переменные величины литерой а.

Из теории дифференциальных урав­нений в частных производных известно, что решение волнового уравнения имеет вид

а = а, (х-ct)+a2(х + сі),

где а, и а2 - произвольные дважды диф­ференцируемые функции от аргументов, приведенных в скобках. Первое слагаемое - это волна, распространяющаяся вдоль оси х в положительном направлении, а второе - волна, распространяющаяся в
обратном направлении. Здесь, как прави­ло, будем иметь дело с прямой волной и опускать слагаемое а2, поэтому в аргумен­те перед х должен стоять знак если перед t стоит "+". Если распространяю­щаяся в направлении оси х волна гармо­ническая (т. е. непрерывные колебания происходят на одной частоте), то она за­писывается формулой

а = A cos[- к(х - cl)] = A cos(col - кх) =

= (11) где А - исходная амплитуда волны; j = л/-Т ; far-col - фаза колебаний; Re - действительная (реальная) часть ком­плексного числа, которую при записи обычно опускают. Непрерывные гармо­нические колебания записывают форму­лой, где фигурирует только время 1:

а = A cos(2tt/1) = A cos(col) = A Re[eyco< ] .

(1.2)

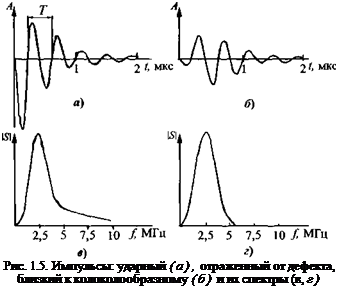
Спектральный анализ. Любой им­пульс можно представить как сумму (или интеграл) непрерывных (гармонических) колебаний разной частоты, имеющих раз­ные амплитуды и начальные фазы (анализ Фурье). Набор таких гармонических коле­баний называют спектром импульса. Он зависит от формы и длительности импуль­са. Чем короче импульс, тем в его спектре больше разных частот (спектр шире) за счет увеличения амплитуд высокочастот­ных (по сравнению с основной частотой) составляющих. Это хорошо видно из срав­нения импульсов, показанных на рис. 1.5, а, б, и их спектров (см. в и г). Спектр им­пульса, приведенный на рис. 1.5, г, значи­тельно уже.

Для непрерывных колебаний спектр - одна частота. Наиболее короткий импульс с наиболее узким спектром - колоколооб­разный, подобный импульсу на рис. 1.5, б, но симметричный, т. е. с одинаковыми фронтом и хвостовой частью. При недос­таточно широкой полосе пропускания системы (например, усилителя УЗ-преоб-

разователя) короткий широкополосный импульс растягивается и приближается по форме к колоколообразному.

При высокочастотном УЗ-контроле электрические импульсы (см. рис. 1.5, а) обычно возбуждают ударным генерато­ром. В процессе преобразования электри­ческих колебаний в акустические и обрат­но форма импульса искажается и стано­вится близкой к колоколообразной (см. рис. 1.5, б).

Колоколообразный импульс описы­вается формулой

а = А ехр{- [vV (/-/0)2]+ М‘ ~ t0)}, (1.3)

где to - время, соответствующее максиму­му амплитуды; v - показатель длительно­сти импульса. Иногда вместо него приме­няют число п колебаний с амплитудами, превышающими 0,1 (20 дБ) от максималь­ного значения:

п = 0,483/v.

Величину т = пТ называют длитель­ностью импульса, а сх - его пространст­венной длительностью. В дальнейшем используются понятия "тонкий слой" и
"протяженная среда". Среду называют протяженной, если путь импульса в ней больше ст. Среду, толщина которой h < схі2 , называют тонким слоем. В нем происходит интерференция в результате многократного отражения импульса от границ.

Ослабление волн. При распростра­нении волны ее амплитуда уменьшается - происходит ослабление волны. Главные причины ослабления: расхождение лучей (точнее, дифракционное расхождение) и затухание волн в среде.

Распространяющуюся в пространстве волну в виде, более полном, чем в (1.1), можно записать так: где г - расстояние, проходимое волной; у = 8 + jk - комплексная постоянная рас­пространения (к - введенное ранее волно­вое число; 8 - коэффициент затухания', который рассматривается позднее); Ь - показатель, зависящий от формы фронта волны (поверхности, на которой фаза вол­ны одинакова).

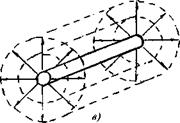
В сферической волне, излучаемой во все стороны сферическим источником (рис. 1.6, б), расхождение лучей происхо­дит в двух плоскостях, поэтому ослабле­ние с увеличением расстояния г идет наи­более быстро: обратно пропорционально расстоянию по закону 1 /г (b = 1). На рис. 1.6 направления лучей показаны сплошными линиями, а фронты волн - штриховыми. Для сферической волны фронты - сферы.

В тоской волне, например, излучае­мой большой пластиной (рис. 1.6,а), фрон­ты - плоскости, лучи не расходятся {Ь = 0). Такая волна ослабевает только под действием затухания. Получить на значи­тельном расстоянии от пластины ограни­ченную плоскую волну в виде пучка па­раллельных лучей не удается. Например, применяя большую пластину или вырезая часть фронта излучаемой пластиной вол­ны с помощью диафрагмы, в действитель­ности получают сложное волновое поле, подобное рассмотренному в разд. 1.3.1. В практике, однако, используют слаборас- ходящиеся пучки лучей, называя их пло­ской волной.

В цилиндрической волне, т. е. волне с цилиндрическим фронтом (например, из­лучаемой боковой поверхностью длинного стержня, рис. 1.6, в), расхождение проис­ходит в одной плоскости (перпендикуляр­ной к оси стержня), поэтому ее амплитуда медленнее ослабевает с расстоянием, чем амплитуда сферической, а именно: обрат­но пропорционально квадратному корню

из расстояния: 1/4г (Ь = 0,5). При рас­смотрении далее волн, локализованных в слое (волн Рэлея и Лэмба), ослабление амплитуды вследствие расхождения в од­ной плоскости происходит как для цилин­дрических волн, т. е. b = 0,5.

Волну с произвольным фронтом можно представить в виде совокупности плоских волн путем разложения в инте­грал Фурье по волновому числу (точнее, волновому вектору) к. Для достаточно длительного акустического импульса, распространяющегося в виде слаборасхо-

Рис. 1.6. Волны с различной формой фронта: а - плоская; б - сферическая; в - цилиндрическая

дящегося пучка лучей, используют фор­мулу (1.1), но уже как приближенную.

Предыдущую формулу можно также записать следующим образом:

a=4e-8v(“^).

/

Такая запись аналогична (1.1), но появился множитель, учитывающий зату­хание волны, вызываемое потерями энер­гии. Уменьшение амплитуды волны под действием затухания пропорционально е_8г, где е = 2,7183... - число Непера (ос­нование натуральных логарифмов).

Коэффициент затухания 8 измеряют в неперах на метр (Нп/м) или неперах на миллиметр пути (Нп/мм). Иногда Нп опускают и пишут 1/мм. Чем больше ве­личина 8, тем больше затухание и тем

меньше множитель е_8г. Когда отноше­ние амплитуд измеряют в дБ, затухание (Sij удобно также выражать в дБ:

(8) = 8,68 8.

Тогда к ослаблению (по различным причинам) амплитуды в децибелах добав­ляют ослабление от затухания, т. е. вели­чину (А'/А0) = (8)г.

Волну, фронт которой перемещается с постоянной скоростью (в случае одно­родной среды), называют бегущей. Она вызывает перенос энергии. Две одинако­вые бегущие волны, распространяющиеся в противоположных направлениях, обра­зуют стоячую волну - периодическое во времени колебание с чередованием в про­странстве узлов (нулей) и пучностей (мак­симумов) амплитуды. В ней перенос энер­гии не происходит. Стоячая волна соот­ветствует условиям установления собст­венных колебаний в объекте. Если ампли­туды встречных волн неодинаковы, воз­никает частично бегущая волна.