Напряжения, деформация и перемещения в балках,. обусловленные объемными изменениями металла
 18 февраля, 2016
18 февраля, 2016  admin
admin Выше было отмечено, что появление временных и остаточных деформаций и напряжений при сварке связано с объемными изменениями металла. Определил количественные зависимости между величиной и распределением объемных изменений в металле, с одной стороны, и величиной и характером распределения деформаций, напряжений и перемещений в балочной конструкции - с другой. Рассмотрим балку таврового сечения с прямолинейной осью и в центре тяжести ее левого торца поместил начало системы XYZ, направив ось X вдоль ее длины, {і оси Y и 2 - вдоль главных осей поперечного сечения**' (рис.2,7,а). Выделим двумя бесконечно близкими сечениями,
х) Здесь под изменением объема понимается его увеличение или уменьшение в направлении оси балки X, т. е. обусловленное стремление продольных волокон балки изменить свою длину, и рассматриваются напряжения и деформации вдоль ЭТОЙ оси.
хх) Будем различать местные системы координат хуг. , связанные со швами, в которых ось х направлена вдоль оси шва, и общую систему координат XYZ, связанную как указано, с балочной конструкцией.
перпендикулярными к оси X, участок балки Ах, отнесем его к единице ДЛИНЫ и изобразим в увеличенном виде (рис.2.7,б).
|
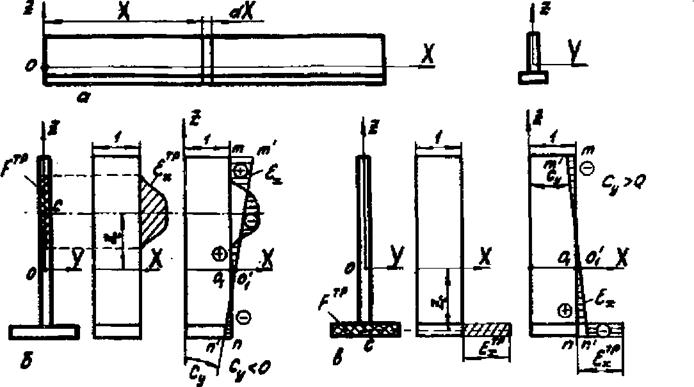
Рис.2.7. Деформации тавровой балки в сечении К вследствие температурных и пластических деформаций |
Предположим теперь, что на части площади сечения балки FTp в результате нагрева или пластической деформации происходит изменение объема металла, вследствие которого продольные волокна в пределах этой площади стремятся удлиниться (или укоротиться) на величину ( tT и tj. - соответ
ственно температурные и пластические деформации). Иначе говоря, при условии обеспечения свободного изменения объема волокна в пределах площади FTp изменили бы свою длину на
величину . При этом погонный объем выделенного участка балки изменился бы на величину AF, если по сечению
балки неодинаковы (рис.2.7,б), и на величину vx-PTpE^ ,
если в пределах площади FTp относительная деформация етх всех волокон одинакова (рис.2.7,в).
Однако свободное изменение объема не обеспечивается, так как, во-первых, волокна, стремящиеся изменить свою длину, связаны с волокнами, которые стремятся ее сохранить, а, во - вторых, смежные участки полосы, испытывающие такие же (иля почти такие же) температурные и пластические деформации, стремятся приобрести аналогичное изменение формы. Иначе
говоря, свободное изменение объема привело бы к тому, что
 плоские сечения, ограничиващие смежные участки искривились бы по закону изменения £Т* , что
плоские сечения, ограничиващие смежные участки искривились бы по закону изменения £Т* , что
в силу сплошности тела. Более того, для стержней и балок справедлива гипотеза плоских сечений, согласно которой сечения, плоские и перпендикулярные к осевой ЛИНИЙ до деформации, остаются плоскими и перпендикулярными к осевой линии и после деформации. Поэтому изменение объема выделенного участка балки вследствие температурных и пластических деформаций (суммарная эпюра которых заштрихована на рис.2.7,6 косыми линиями) вызовет смещение и поворот сечения inn в положение m'n* . Таким образом, прямая m'n' характеризует полные (действительные) относительные деформации £х. Принимая во внимание, что поворот между сечениями, ограничивающими участок балки единичной длины (т. е. отнесенный к единице длины), определяет кривизну CY балки в данном сечении, можно полную деформацию произвольного волокна определить по уравнению прямой
![]() (2.25)
(2.25)
где £х - полная деформация волокна, проходящего на расстоянии Z от оси балки, вызванная смещением и поворотом сечения; &х0 - полная деформация в направлении оси х. - волокна, проходящего через центр тяжести сечения балки (отрезок 0Ч0);
Су - кривизна оси балки относительно оси Y, принимается положительной, если центр кривизны расположен в направлении оси Z (на рис.2.7,б - кривизна отрицательная; на рис.2.7,в - положительная).
Указанное смещение и поворот сечения приведут к возникновению упругих деформаций укорочения и удлинения (их эпюры на рис.2.7 показаны прямой штриховкой) и соответствующих им напряжений. Эти напряжения в пределах площади FTp будут сжимающими, если в этой области происходит увеличение объема металла (е^£> 0), и, наоборот, растягивающими, если металл здесь стремится сократиться ( ££ < 0).
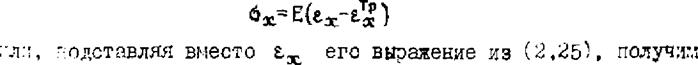 |
В соответствии с (2.8) для определения напряжений в се - чешп; балки имеем соотношение
(2.26)
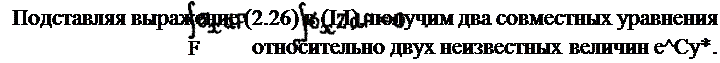 |
Так как выделенный участок балки должен находиться в равновесии, то суша внутренних сил и суша моментов внутренних сил должны быть равны нулю* , т. е. должны быть соблюдены условия равновесия (1,1):
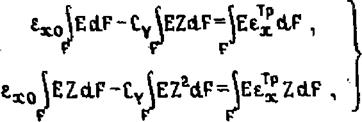 (2.27)
(2.27)
где интегрирование распространяется на всю площадь поперечного сечения F.
В общем случае модуль упругости зависит от температуры и изменяется по сечению балки. Однако, как было отмечено в §2.1, изменением модуля упругости можно пренебречь и принимать его постоянным. Тогда входящие в уравнения (2.27) интегралы становятся равными
W-F 1 Z4F*0 , zadF=IY п WVcLF=irJp F Г Г г
и искомые величины определяются непосре ЯТВЄННО по формулам
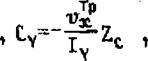
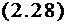 с -■ ж
с -■ ж
tx0 р
где Zt - координата центра тяжести объема v£p ;
JeJzAF
![]() 1*4
1*4
Формулы (2.28) устанавливают количественные зависимости между изменением объема, приходящимся на единицу длины балки (погонным объемом удлинения или укорочения), и параметрами
х) Полагаем, что рассматриваемая балка свободна от внешних нагрузок и является статически определимой.
деформации сечения £х0,Су. Зная последние, можно определить
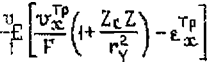 |
||||
полную деформацию и напряжение в произвольной точке сечения. Так, подставляя (2.281! в (2.25") и (2.26), получил соответственно
где ry=|/iv/p - радиус инерции сечения балки.
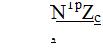 |
|||
Зависл-шости (2,28) можно представить е форме, аналогичной той, которая дается в курсе "Сопротивление материалов" для балок, подвергаемых вне центренному сжатию юш растяжению. действительно, умножая числители и знаменатели правых частей формул (2.28) на модуль упругости, получим
Величина Мтр характеризует величину усилия, которое, будучи приложено в центре тяжести объема ттхр, вызывает те же параметры деформации сечения, что и изменение объема металла. приходящееся на единицу длины балки. Такое написание формул для определения характерных деформаций сечения балки позволяет свести определение деформаций балочных конструкций, обусловленных объемными изменениями металла, к решению задач об изгибе бруса.
Для определения перемещений точек оси балки имеем известные из сопротивления материалов дифференциальные зависимости
![]() d-Ц-х _
d-Ц-х _
cLx 1 Axa "LV
где U-3C, , и, й - продольные и поперечные перемещения точек оси балки. Первая из них (1.2) была получена ранее, вторая непосредственно вытекает из выражения для кривизны. Действительно, кривизна tY и радаус кривизны р изогнутой линии а-*,(х) определяются через ее производные по формуле
а в реальных балках.
Интегрируя первое уравнение (2.33) от 0 до L, находим изменение длины балки по ее центральной оси
L
![]() (2.34)
(2.34)
О
Подставляя значение к0 из (2.28) к учитывая (2.15),
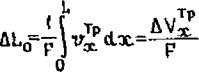 |
имеем
где AVxP = ^irxdLx - изменение объема балки, обусловлен - о
ное удлинением (укорочением) ее продольных волокон вследствие температурных и пластических деформаций.
Проинтегрировав второе уравнение (2.33) в пределах от О до X, находим угол поворота сечения
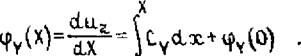 |
о
Интегрируя уравнение (2.36) еще раз от 0 до X, получим уравнение изогнутой продольной оси
х X
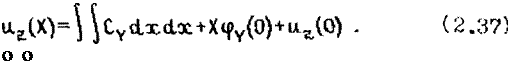 |
Постоянные интегрирования ц>у(0) нДО) характеризуют угол поворота и поперечное перемещение оси балки в нулевом сечении (X = 0).
В общем случае объемные изменения металла распределяются по длине балки неравномерно; могут быть переменными и характеристики поперечного сечения F(X) , Iv(x) , Zt(X) . Поэтому закон изменения параметров деформации сх0 я CY по длине балки иногда сложен, и тогда уравнения (2.34), (2.36), (2.37) интегрируют численно. При этом кривизну Су(Х) представляют в виде фиктивной распределенной нагрузки ^(Х) на фиктивной
 |
балке (рис.2.8,а)х. Тогда полученная фиктивная перерезывающая сила Q.00 и фиктивный момент М(Х) соответственно равны углу поворота сечения іру(Х) и прогибу иг(Х) . Этот прием основан на том, что сила Q. и момент М от распределенной нагрузки тоже определяются аналогичным интегрированием :
Изгибающий момент в сечении X, опре делящий прогиб в этом сечении (рис.2.8,г), равен
Отсюда максимальный прогиб в среднем сечении балки (стрелка прогиба'
• (2-40)
Здесь знаки угла поворота и поперечные перемещения приняты согласно известным правилам сопротивления материалов для перерезывающей силы к изгибащего момента.
Аналогично можно получить формулы для определения прогибов балки для случаев, когда объемные изменения охватывают лишь ее часть или переменны по длине.
|
|
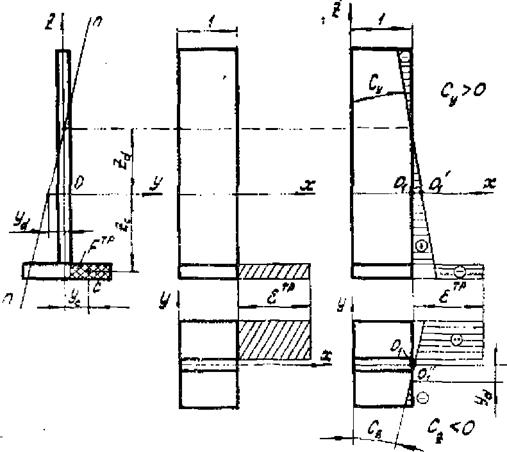
Pi;с.2.9. Несимметричные относительно осей Y и Z температурные к пластические деформации, вызывающие изгиб тавровой балки относительно нулевой
линии п-п
Выше мы рассмотрели симметричную относительно оси Z балку и предполагали, что объемные изменения так:*., симметричны относительно этой же оси. Если эти условия не соблюдены, то изгиб балки происходит относительно так называемой нулевой линии (прямая п-п ), отсекащей на осях отрезки
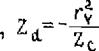 |
|
(рис,2,9):
3 s-том более общем случае к двум параметрам деформация сечения (2,28) добавляется третий Cz - проекция кривизны на ■■■лоскость XOY „ определяемый аналогично Cv с очевидной заменой Zt/lv на Yt/Iz, где Yt - вторая координата ЦТ объема uj. При этом полные деформации в произвольной точ
не сечения могут быть определены со уравнению, аналогичному '.2 .ВО);
В частности, в центре тяжести объема удлинения или укорочения ( Y=Yt, Z = ZC ) полные деформации равны
![]()
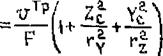 (2.43)
(2.43)
Введем цонятие приведенной площади сечения балки: эта величина характеризует жесткость балки на изгиб, обусловленный объемными изменениями металла:
Если сг-.нтр тяжести объема удлинения (укорочения) совпадает с центром тяжести сечения балки, то Fnp=F ; в противном случае Frp будет тем меньше F, чем больше по абсолютному значению координата Yt и Zt, т. е. чем дальше от центральны^ осей происходят объемные изменения металла.
С учетом (2,44) выражение (2.43) можно переписать в компактном виде, аналогичном формуле для определения полной деформации в центре тяжести сечения балки (с заменой F на
![]()
![]() тр Vx_
тр Vx_
ПР
Расчетные формулы (2.28М2.451 остаются в силе и при учете изменения модуля упругости. Однако величины, входящие в щ;д, должны быть вычислены с весовым множителем Е/Е0 , а
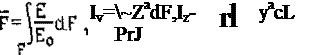 |
||
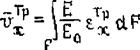 |
||
'тленно:
где vjp - обобщенный погонный объем удлинения (укорочения), см2; F, Iy, Tz - обобщенная площадь и моменты инерция сечения
Л—^ *1
относительно главных обойденных осей сечения балки V 1 см Е0 - значение модуля упругости при нормальной температуре.
Обобщенные главные оси сечения балки Y и I находятся из условий
j-^YcLF'0, j|^ZAF=0 ,^|-Y2dF=0 f (2.4?)
а координаты центра тяжести обойденного объема по формулам
v4Sr„?dF. ч4)1;г4Р ■ 'лж
При вычислении интегралов, фигурирующих в формулах (2.46), следует разбить площадь сечения балки на элементы, определить температуру центра тяжести этого элемента (и. в
зависимости от нее - модуль упругости) и заменить интегралы соответствующими суммами.
Учет изменения модуля может привести к существенным поправкам при рассмотрении деформаций балки малой жесткости і: высоких уровнях нагрева и при применении металлов с модулем упругости, резко падающим с повышением температуры. Поскольку весовые множители входят в подынтегральные выражения как числителя, так и знаменателя основных расчетных формул (2.23), то его учет обычно приводит к незначительным поправкам, а влияние может быть отнесено ко вторичным эффектам.
Расчетные формулы, полученные в настоящем параграфе, являются общими в том смысле, что связывают объемные изменения металла с напряжениями, деформациями и перемещениями балочной конструкции независимо от причины, вызывающей эти изменения. Их можно применить не только для определения деформаций, напряжений и перемещений, возникающих при сварке, но и при других технологических процессах, связанных с объемными изменениями металла. Действительно, при выводе указанных формул не делалось никаких ограничений в отношении характера распределения объемных изменений металла в балке. Поэтому они справедливы для определения как временных, так и остаточных сварочных деформаций и перемещений балочных конетрук-
х)
дан от продольных и поперечных швов,, Температурные и пластические деформации, возникапцие в процессе сварочного нагрева и посіле дующего остывания, непрерывно изменяются. Очевидно, что после полного остывания температурные деформации становятся равными нулю, а пластические завершают свои изменения, превращаясь в остаточные. Следовательно, для расчета остаточных напряжений следует найти лишь распределение по сечению полосы остаточных пластических деформаций. Решению стой задачи, т. е. определению остаточных пластических деформаций, мы уделим основное внимание. Оно затрудняется двумя обстоятельствами;
Р определение остаточных пластических деформаций тре - ііуст изучения истории их развития (см. § 2.2);
21) пластические деформации зависят от полных деформаций (см. уравнение (2.6)) , в то время как для определения последних необходаио знать распределение пластических деформаций.
Первое затруднение преодолевается обычно путем постепенного (пошагового) рассмотрения процесса, т. е. путем изучения упругопластических деформаций в сечении в отдельные последовательные моменты времени. Для преодоления затруднения, обусловленного взаимосвязью между полными и пластическими деформациями, используют на каждом шаге по времени методы последовательных приближений. Однако такой путь решения задачи является весьма трудоемким, и потому он годится только при использовании ЭВМ (см. гл.7). Учет ряда особенностей процесса развития упругопластических деформаций при сварке позволил разработать более простые методы решения указанной задачи, которые излагаются в 4-й главе.
Следует, однако, отметить, что в районе резкого изменения обтемннх изменений по длине балки (начало и конец зто - дольного^шва, район поперечного шва, зона вблизи свароч - н°й дуг:г ее сечения искривляются и полученное решение, основанное ні-' гипотезе плоских сечений, дает погоешно - стп.

 Опубликовано в
Опубликовано в