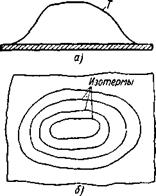
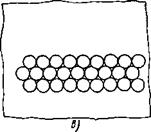
Предположим, что некоторая область бесконечной упругой пластины нагрета по какому-либо закону, заданному численно йли аналитически (рис. 18, а и б), и необходимо определить распре­деление напряжений. Разбиваем всю нагретую область условно

на кружки с наиболее плотной упаковкой (рис. 18, в). Можно представить, что область каж­дого из кружков окружена неко­торыми фиктивными силами R — <хТЕ

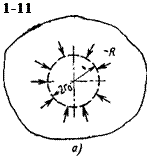
(рис. 19, а), которые не

а — распределение температур; о — изотермы в пластине; в — разбивка области нагрева нз отдельные небольшие области

позволяют данному кружку расширяться при нагреве, Т — тем- ература центра кружка. Очевидно, что если каждый из кружков Удерживать такими силами, то никаких перемещений не возникнет.

^ В. А. Винокуров 33

В пластине будут действовать только гидростатические напря­жения

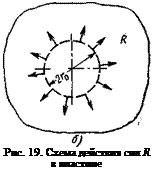
Ввиду того что никаких фиктивных сил в теле не существует, их необходимо снять, приложив силы противоположного направ­ления (рис. 19, б). От сил одного кружка согласно уравнениям (13) и (14) возникнут напряжения: а) в самом кружке

где гр — расчетный радиус приложения сил R, который должен быть несколько больше действительного радиуса кружка, чтобы учесть «плотность упаковки» кружков, связанную с наличием «пустот» между отдельными кружками. Расчетный радиус связан с радиусом кружка л, при плотности расположения кружков, показанной на рис. 18, в, следующей зависимостью:

2/3

Применяя метод суперпозиции (наложения) полей напряжений (39) и (40) от всех кружков при снятии фиктивных СИЛ, МОЖНО получить распределение напряжений при заданном неравномер­ном нагреве пластины. Операцию суммирования напряжений ввиду ее трудоемкости и продолжительности целесообразно производить при помощи ЦВМ. Для этого в ЦВМ хранится для каждого кружка следующая информация: координаты центра кружка х и у, ве­личина R, компоненты напряжения ох, ау и хху. По мере снйтия сил R к напряжениям ах, оу и тхУ каждого кружка добавляются напряжения Да*0; ДаУо и Дт*^, возникшие от снятия сил R у дру­гих кружков.

Перевод напряжений аГо и <т(о, выраженных в полярных коор­динатах, в декартовы координаты производится по формулам

1-ц А_ п А*2 , 1 ~Ц Г1 » Ду2 .

2 ' Ara * А г* "г 2 Аг» А Д г* *

r*n _ Дх Д і/

Аг2 = Ал:2 + Ay2; Ах = хп — л:0; Ау = уп — Уо;

х, уп — координаты центра кружка, в который направляются AOj:0; А о Уо; Аххул;

х0, у0 — координаты центра кружка, у которого снимаются фиктивные силы R.

Если пластина не является бесконечно большой или в ней имеются какие-либо отверстия, то после получения температур­ных напряжений в беско­нечной пластине необхо­димо учесть наличие отвер­стий или ограниченность размеров пластины. Для этого область отверстия разбивается на кружки и предполагается, что ме­талл отверстия не. воспри­нимает никаких упругих деформаций, т. е. от = 0. Иными словами, необходимо решить пластическую задачу, когда имеется область идеально пластич­ного металла, у которого ат = 0.

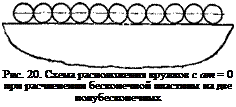
На рис. 20 приведен пример разбивки на отверстия границы полубесконечной пластины при выполнении указанного гранич­ного условия.

Если поле температур обладает резко отличающимися градиен­тами температур, то разбивка пластины на кружки одинакового Размера оказывается нерациональной. Например, если необхо­димо получить распределение напряжений при нагреве пластины

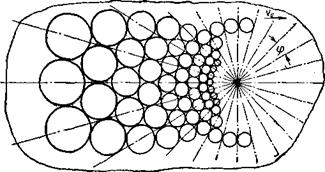
движущимся источником тепла с учетом теплоотдачи, что трудно выполнить аналитически, то разбивку целесообразно выполнить так, как показано на рис. 21. В этом случае в зоне больших гра­диентов температуры имеются кружки малого диаметра, а в об­ласти малых градиентов — большого диаметра. Зависимость рас­четного радиуса кружка от фактического при данной упаковке кружков выражается формулой (43)

(43)

где

Ф — угол между смежными лучами, проходящими через центры кружков (см. рис. 21).