Предположим, что нужно рассчитать процесс распро­странения тепла при ручной электродуговой наплавке валика на массивную плиту значительных размеров. Прежде чем приступить к рассмотрению этого случая, следует выбрать расчетные схемы тела и источника тепла.

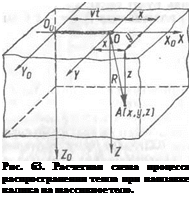
Плиту будем считать пол у бесконечным телом, поскольку размеры ее таковы, что все имеющиеся граничные поверхности, кроме плос­кости, на которую производится наплавка, не искажают теплового поля. Электрическую сварочную дугу примем за точечный подвиж­ный постоянно действующий источник тепла. Тепловую мощность сварочной дуги в процессе наплавки валика примем постоянной. Тогда поставленную задачу в идеализированном и схематизиро­ванном виде можно сформулировать следующим образом: «Рассчи­тать процессы распространения тепла при нагреве поверхности полубесконечного тела точечным постоянно действующим подвиж­ным источником тепла постоянной мощности».

В первый момент после зажигания дуги количество вносимого тепла превышает теплоотвод и область разогрева увеличивается. Такой процесс называется теплснасыщгнием. В этот период разо­грев детали и проплавление основного металла могут быть недоста­

точными. В результате начало шва обычно бывает менее прочным, чем последующие участки.

Если дуга горит непрерывно и перемещается с постоянной ско­ростью, то наступает момент теплового равновесия: количество тепла, вводимого в тело дугой, становится равным количеству отведен­ного тепла. После достижения равновесия подвижное тепловое поле сохраняет свой характер. Такое тепловое состояние называется предельным, или квазистационарным.

Уравнение предельного состояния для процесса распределения тепла от точечного источника постоянной мощности, движущегося с постоянной скоростью по поверхности полубесконечного тела, отнесенное к подвижной системе координат, может быть выведено

из ранее приведенных соотношений и после всех преобразований и упрощений приобретет следующий вид:

_ vx__ vH

Т(*>х) = Ше 20 20 • 0V.27)

где R — расстояние точки А, в которой определяется темпера­тура, от начала О координат подвижной системы (рис.63); х — абсннсса точки А в подвижной системе координат; v — скорость сварки, см/сек.

Проанализируем полученное выражение. Предположим, что источник тепла неподвижен, т. е. v = 0. Тогда е в нулевой степени равно единице и выражение (IV.27) преобразуется в

Чи

2 nlR-

Температура точек тела в этом случае обратно пропорциональна их расстоянию от источника тепла R, так как qu и К приняты постоянными. Точки, равноудаленные от источника тепла, имеют одинаковую температуру, т. е. изотермические поверхности пред­ставляют собой концентрические полусферы.

, ------- и у vianuBHJ ъ, 4 ГО

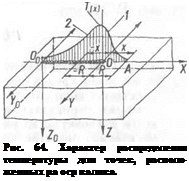
при увеличении скорости перемещения изменение температур по оси X происходит таким образом, что передняя ветвь / кривой (рис. 64) становится круче, тогда как ветвь 2 за источником тепла остается неизменной. В самом деле, для точек, лежащих на оси X, расстояние R от точки О равно (4-х), если точка расположена перед дугой, и (—х), если она — за дугой. Положив для передней ветви температур R — х, получим

Очевидно, увеличение v уменьшает значение Т (х), т. е. с увеличе­нием скорости наплавки передняя ветвь будет более крутой.

Для задней ветви температур Т (х) подстановка R — —х в вы­ражение (IV.27) дает

Т (х) =

т. е. здесь Т (х) не зависит от скорости движения источника. Харак­тер задней ветви кривой температур при изменении скорости на­плавки остается постоянным, как это и предполагалось ранее.

В сечениях, перпендикулярных к шву, тепло от валика распро­страняется равномерно во все стороны, благодаря чему изотермы в таких сечениях представляют собой концентрические полуокруж­ности.

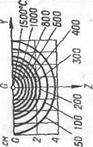
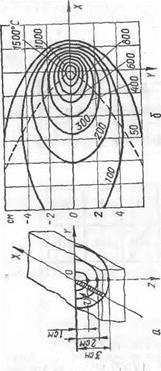
Общая картина температурного поля предельного состояния при наплавке валика на массивное изделие показана на рис. 65, заимствованном из монографии Н. Н. Рыкалина [22]. Изотермы вы­числены для q = 1000 кал! сек, и = 0,1 см/сек, а — 0,1 см2/сек, К — — 0,1 кал/(см • сек • °С). На рис. 65, о показана схема наплавки; на рис. 65, б — изотермы на поверхности тела и кривая точек с максимальными температурами (штриховая линия); на рис. 65, в — изотермы в поперечном к валику сечении; на рис. 65, г —■ распре­деление температур по прямым, параллельным оси Y в сечении YOZ и удаленным от нее соответственно на R —V Xі + у2 — 0,1, 2, 3 см; на рис. 65, д — распределение температур по прямым, па- раллельным оси X в сечении X0Y и удаленным от нее соответственно на R = Vг2 + у2 — 0, 1, 2, 3 см. Максимум температур в точках, удаленных от оси перемещения дуги, достигается не в тот момент, когда дуга находится в плоскости, проведенной через данную точку перпендикулярно к оси X, а несколько позже (рис. 65, о). На рис. 65, б на плоскости через соответственно нанесенные точки максимумов штриховой линией проведена кривая — след поверх­ности максимальных температур, перемещающейся вместе с полем в направлении движения источника. Область, находящаяся впере­ди поверхности максимальных температур, нагревается, область позади нее охлаждается. Приведем примеры расчета.

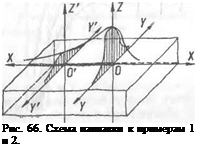
Пример 1. Рассчитать, как распределяются температуры по оси X валика и по оси К, перпендикулярной к направлению сварки, при наплавке на массив­ную стальную деталь (рис. 66), Режим наплавки: / = 300 a; U — 25 в; с — = 10 м/ч = 0,278 см/сек.

В качестве расчетной схемы изделия примем полубесконечное тело. Расчет­ная схема источника тепла — точечный непрерывно действующий подвижный источник.

Для расчета иагрева тела данным источником используем формулу (IV.27):

у (X+R)

гше 20 •

Примем следующие средние значения теплофизических величии для сталиі

с = 0,128 кал/(г •°С); а — ~ =
*6ЛШГтГв-0'1 смг/сек-

Примем для ручной электродуго - вой сварки % = 0,75; qu = 0,24 ■ 25 х X 300 ■ 0,75 = 1350 кал/сек.

При расчете температур точек, ле­жащих на оси позади движущейся дуги, R = —х. Тогда

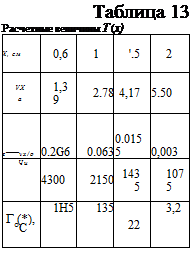
Выбрав значения х — 1,5; х = 2 и т. д. в соответствии с табл. 12, опре­делим;

Т (1.5) - -0- —т-с = 1435 ‘С и т. д.

R — х, см	1,5	2	3	4	6	8	10
Т (х), °С	1435	1075	717	537	358	269	215

2 - 3 14 • 0,1 ■ 1,5 Расчетные величины Т(х)

Таблица 12

При определении температур точек, лежащих на оси впереди движущейся дуги, будем иметь в виду, что для иих R — x. Тогда

Задаваясь значениями х нз табл. 13, найдем температуру (табл. 13).

Распределение температур тела по оси Y найдем на основании следующих соображений. Воспользуемся для расчета формулой (IV.27), учитывая, что для точек оси Y в подвижной системе координат, начало которой совмещено с источ­ником тепля, всегда х = О. Значит -

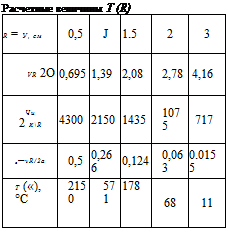Задаваясь различными значениями R, которые для точек, лежащих на оси V, равны у, определим температуры (табл. 14).

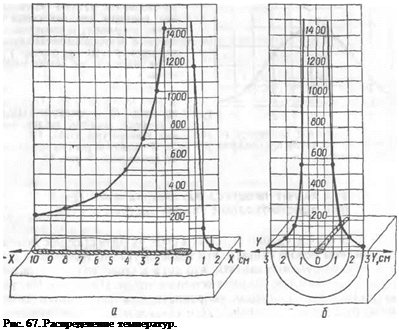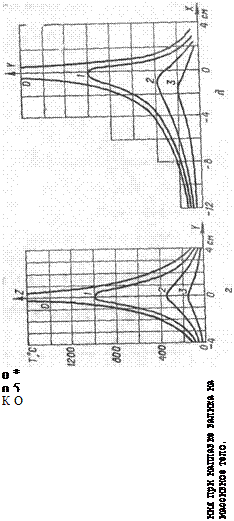
Результаты произведенных расчетов Т (х) представлены графически (рис. 67, а, б).

Пример 2. Исходя из условий, заданных в предыдущем примере, рассчитать характер распределения температур в сечении Y'Y' (рис. 66), перпендикулярном к шву, через 20 сек после прохождения этого сечения дугой.

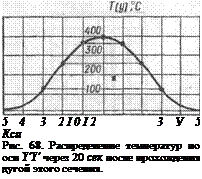Для расчета воспользуемся той же формулой (IV.27). Поскольку она выведена для подвижной си­стемы координат, перемещающейся вместе с источником тепла (дугой), то через / = 20 сек сечение Y'Y' будет отстоять от начала коорди­нат на х = Ы = 0,278 • 20 =5,66 см.

Задаваясь значениями у, опре­делим R = + Уг- Подставив

значения R в формулу (IV.27) и проведя расчеты, найдем иско­мые температуры (табл. 15).

Результаты расчета представле­ны графически на рис. 68.