Основные параметры СУВ
 30 августа, 2016
30 августа, 2016  Mihail Maikl
Mihail Maikl В самом общем случае баланс воды в батарее ТЭ характеризуется рядом параметров, например температурой батареи, концентрацией электролита, количеством удаляемой и образующейся воды, зависящих от большого числа внешних воздействий (давление, ток нагрузки, расход водорода и т. п.). В общем виде установившееся состояние СУВ будет описываться довольно громоздкой системой уравнений [5.9]
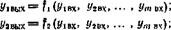 (5.17)
(5.17)
![]() Уі вых— ft (Уівх> Угвх> ••• > Упг вх)>
Уі вых— ft (Уівх> Угвх> ••• > Упг вх)>
где у 1Вых, г/гвых........ г/гвых — выходные параметры системы; г/1Вх,
1/2ВХ........... Утъи — внешние воздействия на систему.
Анализ данной системы уравнений с учетом влияния всех параметров иа условия массообмена в батарее и конденсаторе на данном этапе представляет значительные трудности. Задача существенно облегчается, если принять следующие допущения:
1. Вольт-амперная характеристика батареи ТЭ в рассматриваемом диапазоне изменения параметров линейна и не зависит от температуры и концентрации электролита.
2. Процесс массообмена в контуре протекает при изотермических условиях, т. с. при фиксированных температурах батареи и конденсатора, причем батарея и конденсатор при этом рассматриваются как «черный» ящик. Параметры пароводородной смеси на выходе из батареи определяются решением системы уравнений (5.10),
(5.15) , а параметры смеси на выходе из конденсатора — температурой конденсации.
3. Расход водорода в контуре циркуляции постоянный.
4. Водород и электролит в ТЭ находятся в тепловом и массообменном равновесии, т. е. влагосодержание зависит только от температуры и концентрации электролита.
Принятые допущения позволяют, не нарушая существа физических процессов, протекающих в СУВ, проанализировать взаимное влияние параметров на баланс воды в ТЭ батареи.
С учетом принятых допущений система уравнений (5.17) примет вид:
напряжение ТЭ
![]() U=Eo~af,
U=Eo~af,
где £о — напряжение элемента при нулевом токе нагрузки; I — ток нагрузки; а—коэффициент пропорциональности;
количество образующейся воды согласно закону Фарадея
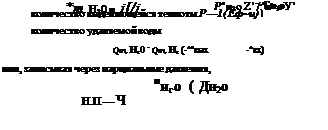 |
|
Q*m, н, о = - у 'ЗбСО = 0,336/; (5.19)
![]() Н2—расход циркулирующего водорода; ръцо — парциальное давление паров воды в потоке водорода на выходе из батареи; ркд о — парциальное давление паров воды на выходе из конденсатора. Давление паров еоды 0 является функцией температуры и
Н2—расход циркулирующего водорода; ръцо — парциальное давление паров воды в потоке водорода на выходе из батареи; ркд о — парциальное давление паров воды на выходе из конденсатора. Давление паров еоды 0 является функцией температуры и
концентрации электролита, которую, предполагая справедливость закона Рауля для рассматриваемого диапазона концентраций электролита, можно записать
PS НаО— РнгО^ —N),
где о — давление паров над водой при температуре электролита; N — содержание гидроокиси калия в электролите, моль/л.
Давление паров ркн о на выходе из конденсатора является функцией только температуры и определяется выражением
1п РкНгО ~ ~~ (5.24)
где г — теплота парообразования; R—универсальная газовая постоянная; С — константа.
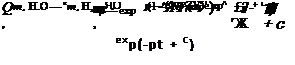 |
|
С учетом (5.23) и (5.24) уравнение (5.22) можно переписать в виде
где Тэ и Тк—соответственно температуры ТЭ и конденсатора.
Поскольку рассматривается статический режим работы, т. е. количество образующейся воды равно количеству удаляемой, можно
записатъ ~ Qm, H,o
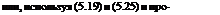
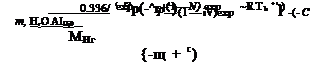 |
|
водя преобразования,
 |
 |
Уравнение материального баланса (5.26) определяет взаимосвязь основных параметров системы удаления воды: тока нагрузки, расхода водорода, температур батареи и конденсатора, равновесного значения концентрации электролита, давления в контуре. Влияние основных параметров системы удаления воды (температуры
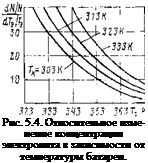
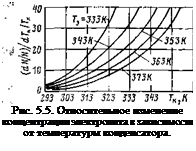
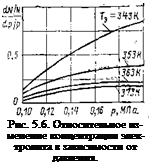
батареи Гэ, температуры конденсатора Тк и давления в контуре р) на диапазон изменения относительных концентраций электролита характеризуется выражениями (5.27) — (5.29), полученными дифференцированием уравнения (5.26),
![]()
dN/N — N г 1ПпГэ = N R7
Наибольшее влияние на относительное изменение концентрации электролита оказывают температуры батареи и конденсатора. Давление в контуре циркуляции влияет значительно слабее (рис. 5.4— 5-6). . Ї,. -
Для упрощения расчетов с целью
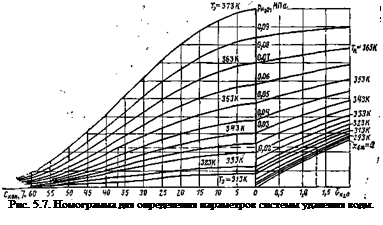 |
Определения необходимых параметров. удобно использовать номограмму (рис. 5.7), которая представляет собой графическое решение уравнения (5.26). В левой части номограммы приведены кривые зависимости давления паров воды над электролитом для различных температур и концентраций электролита, построенные по справочным данным и экстраполированные по правилу Бабо [5.10], в правой части — кривые зависимости количества воды GH 0," удаляемой 1 кг сухого водорода, для ряда значений температур за конденсатором.

 Опубликовано в
Опубликовано в