Любая динамическая система характеризуется притоком вещества или энергии и их стоком. Если приток равен стоку, то система нахо­дится в равновесии. Уровень в баке Я и в паровом котле будет неиз­менным, если в первом случае приток воды в баке Gnp (рис. 9, а) равен

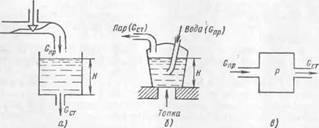
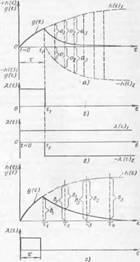
Рис. 9. Объекты автоматизации гидравлической (а), тепловой (б) и пневматической (в) установок

стоку GCT, а приток воды в паровой котел будет равен количеству поды, выносимой в парообразном состоянии (рис. 9,6). Только при таких условиях уровень будет неизменным. Постоянное давление в пневматической емкости установится только при условии G„p = Сст (рис. 9, в).

При нарушении условия равновесия регулируемые параметры (уровень, температура и давление) будут изменяться в каждую еди­ницу времени. Характер этого изменения мы рассмотрим на примере гидравлической уста новки (рис. 9,а).

Увеличим расход воды на притоке с помощью клапана и характер изменения расхода изобразим графически (рис. 10, а). Пс оси абсцисс отложим вре­мя (например, в секундах), по оси ординат — расход воды (м3/ч).

До момента внесения возму­щения расход жидкости на при­токе равен расходу на стоке.

В момент времени t — 20 с из­меним скачком расход жидкости на притоке с 4 до 6 м*/ч. С уве­личением GIip уровень И воды начинает расти с постоянной скоростью (как показано пунк­тирной линией аб), но увели­чение количества жидкости в емкости и ее общей массы уве­личивает напор, с которым жидкость проходит через трубу стока, т. е. увеличение уров­ня приводит к увеличению на­пора, а тот в свою очередь увеличивает GCT и тем самым уменьшает гкорость роста уровня. Поэтому рост уровня Н изобразится кривой ас. В момент, когда расход на стоке, увеличиваясь, станет равным расходу на притоке, уровень перестанет расти и установится на ио­ном значении. Система придет в новое устойчивое состояние (устано - шгвшееся значение). Переход системы из одного устойчивого состоя­ния в другое характеризует динамические свойства объекта, которые должны учитывать наладчики при настройке замкнутой системы авто­матического регулирования.

Кривая перехода технологического параметра, в данном случае уровня, из одного устойчивого состояния в другое при ступенчатом розмущении называется разгонной (переходной) характеристикой ре­гулируемого параметра. А свойство системы достигать устойчивого состояния после приложения длительного возмущения без вмешатель­ ства управляющего устройства называется самовыравниванием (са­морегулированием) .

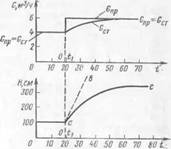
Рис. 10. Получение разгонной ха­рактеристики регулируемого пара­метра:

а — графики изменения параметров и раз­гонная характеристика. б—диаграммы прохождения сигналов

Если параметры процесса изобразить кружками, а влияние пара­метров друг на друга — стрелками, то получим диаграмму прохож­дения сигнала (рис. 10, б), которая вскрывает природу саморегули­рования.

Знаком «4-» над стрелкой обозначим положительную связь, а зна­ком «—» — отрицательную. Диаграмма читается так: увеличение Gnp

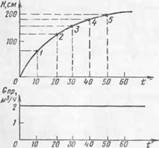
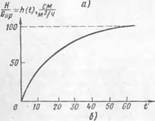
Рис. 11. Построение разгонной (а) и временной (б) характеристик

увеличивает Я, увеличение Н уве­личивает напор, увеличение напо­ра увеличивает GCT, увеличение GCT уменьшает уровень. Диаграм­мы прохождения сигнала позволя­ют вскрыть внутреннюю структуру динамической системы.

На диаграмме прохождения си­гнала видна отрицательная обрат­ная связь, осуществляющая само - выравнивание (отрицательный кэн - тур: Н — напор — GCT — Н). Со - і вокупность прямой цепи и обрат­ной связи называется контуром. При отрицательной обратной свя­зи контур отрицательный, при по­ложительной—положительный. На­личие отрицательного контура всегда характеризует стабилизиру­ющие свойства системы. В системе как бы существует внутренний ре­гулятор, который и обеспечивает стабилизацию параметра на новом уровне.

Для исключения из опыта про­изводственных помех (неконтроли­руемых возмущений) на действую­щем оборудовании всегда снимают несколько разгонных характерис­тик, причем точно выдержать одинаковые величины возмущений при каждом опыте не всегда удается, а при разных возмущениях уста­новившиеся значения будут различными. Чтобы привести несколько разгонных характеристик к одному возмущению, их необходимо пе­рестроить следующим образом.

За начало отсчета времени принимается момент внесения возму­щения, а за начало отсчета уровня — уровень до внесения возмущен ния, т. е. разгонная характеристика переносится в начало коорди­нат (рис. 11, а). Затем несколько текущих значений уровня, соответ­ствующих точкам 1—5, делят на величину возмущения (2 м3/ч). По­лученная таким образом характеристика (рис. 11,6) обозначается h (t) и называется временной. Она представляет собой кривую изме і. опия выходной величины объекта (например, уровня) во времени, полученную в результате единичного входного ступенчатого возму­щения при условии, что до момента приложения этого возмущения система находилась в покое (т. е. других возмущений не было).

Временная характеристика при входном сигнале прямоугольной формы. Принцип наложения

Для многих технологических процессов недопустимы значитель­ные отклонения регулируемых величин от заданных значений. В этом случае при снятии временных неличину входного возмущения. Пр тлт эксперимента будут оказывать существенное влияние нерегистри - руемые внутренние и внешние воз­мущения (помехи), всегда имеющие место на реальных объектах. Для большинства объектов химических и нефтехимических производств максимально допустимые возмуще­ния по величине соизмеримы с уровнем помех и результирующке характеристики будут отражать действительные со значительными погрешностями.

Временные характеристики сис­тем на таких объектах (рис. 12, а) снимают следующим образом. Сту­пенчато увеличивают (уменьшают) входную величину (рис. 12, б) и раньше момента достижения сис­темой нового равновесного состоя­ния снимают возмущение. Таким образом рассматривают реакцию системы на входное возмущение прямоугольной формы.

Построим график реакции сис­темы на такое возмущение, для этого импульс представим в виде двух равных по величине, но про­тивоположных по знаку ступенча­тых возмущений, приложенных в характеристик приходится уменьшать.

Рис. 12. Временная характеристика при входном сигнале прямоугольной формы:

и—построение импульсной характеристи­ці!. 6 — импульсное возмущение, в — раз­ложение импульсного возмущения на две г1 упенчатые составляющие, г — построе­ние временнбй характеристики по импульс­ной

моменты t = 0 и t = /х так, как это представлено на рис. 12, в, где ступенчатые возмущения обозначены X (/), и Л, (/)г (на рис. 12 и в даль­нейшем мы ие будем наносить на оси координат шкал}' размерности)

Реакцию системы представляют двумя соответствующими времен ными характеристиками h (t)г и h (t)2, полученными при ступенчатых возмущениях соответственно К (t)j и Я (/)2.

Для построения характеристики g (t) достаточно алгебраически сложить ординаты временных характеристик h (t)1 и h (t)2, т. е. h (t)t— — h (t)2 = g(t).

Ось абсцисс делят на произвольное число отрезков и из ординат A (/)j, соответствующих концу каждого отрезка, вычитают соответ­ствующие ординаты временной характеристики h (t)z (а,, а2, £з и т. д.). Полученная таким образом характеристика полностью отражает ди­намические свойства системы, но имеет значительно меньшее отклоне­ние от исходного режима, чем временная.

Построение характеристики по двум независимым возмущениям хорошо иллюстрирует принцип наложения. Сущность принципа на­ложения может быть сформулирована следующим образом: реакция системы на сумму входных воздействий равна сумме реакций на каж­дое из этих воздействий, взятых в отдельности.

Системы автоматического регулирования, для которых применим принцип наложения, называются линейными системами. В настоящем курсе рассматриваются в основном линейные системы, и этот прин­цип применим во всех рассматриваемых ниже системах Случаи не­линейных систем будут оговорены особо.

В практике наладочных работ возникает обратная задача — по импульсной характеристике, полученной экспериментально, постро­ить разгонную характеристику, т. е. необходимо, зная g (t), найти h (/),.

Из приведенного выше выражения следует, что h (t)l = g (t) -H + h (О*.

Из условия построения мы знаем, что h (t)2 точно соответствует j (совпадает) h (/),. но сдвинута по оси времени на величину % (рис. 12, а), т. е. на величину длительности импульса. Сокращенно это можно записать h (t)2 = h (t—т)г. Следовательно, h {t)x = g(t) -H 4- h (t—x)i - Для построения временной характеристики необходимо ось времени разбить на отрезки, равныет, и затем суммировать орди­наты перпендикуляров, восстановленные из точек xj, т2, т3, ... , как показано на рис. 12, г, и к каждому последующему значению g (/?) прибавлять предыдущее значение ординат (Ьх, Ь2, 63, ...).

В реальных условиях действующего, а тем более только что пу­щенного технологического процесса не всегда возможис обеспечить испытания по снятию временных характеристик. В этих случаях для изучения динамических свойств автоматических систем применяют частотные характеристики.