Electrically conductive high-reflectivity omnidirectional reflectors are highly desirable. With air as the outside medium, omnidirectional reflection characteristics can be demonstrated by using high-contrast DBRs. The high-contrast materials Si (n «3.5 at X = 1 |jm) and SiO2 (n «1.46) are natural candidates for such ODRs. The optical properties of Si / SiO2 distributed Bragg omnidirectional reflectors (DB-ODRs) and other material systems have been investigated (Chen et al., 1999; Bruyant et al., 2003).

Whereas omnidirectional TE reflectivity is readily obtained in DB-ODRs, the Brewster angle, at which the TM reflectivity decreases to zero, is an impediment in achieving omnidirectional characteristics for TM waves. An outside angle range of 0° < 0 < 90° (in a low - index outside material such as air) results in an angle range 0° < 9 << 90° inside the material (i. e. inside the DBR). The inside range may not include the Brewster angle under which circumstances a DBR becomes omnidirectionally reflective.

Highly omnidirectional reflection characteristics were also obtained with DB-ODRs using polystyrene and Te layers (Fink et al., 1998). Owing to the very large difference of the refractive indices, npolystyrene = 1.8 and nTe = 5, the interfacial Brewster angle 9B is not accessible from

light incident from air, resulting in a complete photonic bandgap in the wavelength range from 10 to 15 цш.

Another intriguing approach uses birefringent polymers with two different refractive indices parallel and vertical to the layer planes (Weber et al., 2000). By adjusting the differences between the vertical and in-plane indices, the value of the Brewster angle can be controlled. Brewster angles up to 90° (grazing incidence) and even imaginary values are possible, resulting in a high reflectivity for TM-polarized light at virtually all angles of incidence.

Unfortunately the applicability of the above-mentioned DB-ODRs to LEDs is limited due to the insulating electrical characteristics of the constituent materials.

Metallic layers are capable of reflecting light over a wide range of wavelengths and incident angles with the high-reflectivity band being limited to frequencies below the plasma frequency of the free-electron gas (for historical references, see Drude, 1904; Lorentz 1909). However, electron oscillations induced by the incident light waves not only result in reflection but also in absorption caused by electron-phonon scattering. Thus, pure metal reflectors have significant

reflection losses, particularly when used on high-index materials.

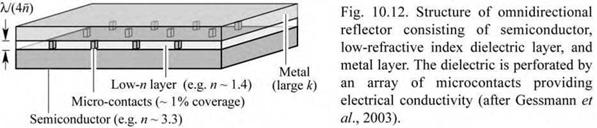
An electrically conductive reflector that has high-reflectivity and omnidirectional characteristics is shown in Fig. 10.12 (Schubert, 2001, 2004). It consists of three layers, a semiconductor, a dielectric layer, and a metal layer (triple-layer ODR). The dielectric layer is perforated by an array of microcontacts that provide electrical conductivity. The dielectric layer should have a refractive index as low as possible to provide a high index contrast to the semiconductor and the metal. The metal has a complex refractive index with a large extinction coefficient.

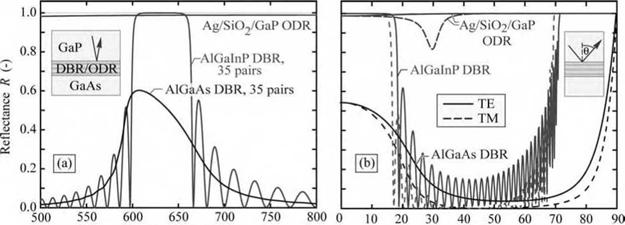
Wavelength X (nm) Angle 0 (°) Fig. 10.13. (a) Calculated reflectance at normal-incidence versus wavelength and (b) reflectance versus angle of incidence for an omnidirectional reflector (ODR), a transparent AlGalnP/AllnP DBR, and an absorbing AlGaAs/GaAs DBR (after Gessmann et al., 2003)

The reflectivity of the triple-layer ODR calculated by the matrix method is shown in Fig. 10.13 versus wavelength and versus angle along with the reflectivity of two DBRs (Gessmann et al., 2003). The triple-layer ODR provides a broad reflectivity and omnidirectional characteristics. A small dip in the reflectivity is found for the TM wave at an incidence angle of

about 30° due to the reduced reflectivity of the semiconductor/dielectric interface at the Brewster angle. The angle-integrated reflectivity of the triple-layer ODR is very high and can exceed 99%.

At normal incidence (9 = 0), the reflectivity of the triple-layer ODR can be calculated analytically and is given by

Rodr = [ns - nli)(nli + nm) + (ns + nli)km] + ]ns - nli)km + (ns + nli)(nli - nm)]2 (10 30)

[(ns + nli )(nli + nm) + (ns - nli )km ]2 + [ns + [)km + (ns - nli)(nli - nm)]2

where nli and ns are the refractive indices of the dielectric and semiconductor, respectively, and Nm = nm + i km is the complex refractive index of the metal. The equation applies to a thickness of X0 / (4 nli) for the low-index dielectric layer, i. e. a quarter-wave layer. For an AlGaInP/SiO2/Ag structure emitting at 630 nm, the equation yields a normal-incidence reflectivity Rodr(9 = 0) of 98.8% compared to a value of 96.1% for a structure without a dielectric layer.

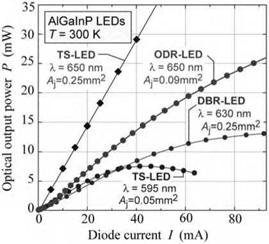
650 nm AlGaInP LEDs using a triple-layer ODR have been demonstrated. The surface coverage of the microcontact array was 1%. The light-output power versus current characteristics of the ODR-LED and several reference devices are shown in Fig. 10.14 (Gessmann et al., 2003). Comparison of the ODR-LED output characteristics with those of DBR-LEDs yields that the ODR-LED provides higher output powers.

Fig. 10.14. Light-output power versus injection current of different types of LEDs. The ODR device has a higher output power than the DBR device (after Gessmann et al., 2003).

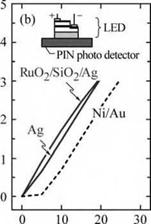
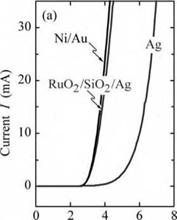
ODR-LEDs have also been demonstrated in the GaInN material system (Kim et al., 2004). The ODR consisted of a RuO2 ohmic contact to p-type GaN, a quarter-wave-thick SiO2 low - index layer perforated by an array of microcontacts, and an Ag layer. Calculations predict a 98% angle-averaged reflectivity at X = 450 nm for an GaN/SiO2/Ag ODR, much higher than that for
an Al0.25Ga0.75N/GaN distributed Bragg reflector (49%) and Ag (94%). It was shown that the RuO2/SiO2/Ag ODR has a higher reflectivity than Ni/Au and even Ag reflectors, leading to a higher light extraction efficiency of the GaInN ODR-LED. The electrical properties of the ODR - LED were found to be comparable to those LEDs using conventional Ni/Au contacts. A comparison of the electrical and optical characteristics of the GaInN ODR device is shown in Fig. 10.15.

Forward current I (mA)

Fig. 10.15. Current-voltage and 1 ight-output-versus-current char­acteristics of a GaInN LED with a GalnN/RuCb/SiCb/Ag omni­directional reflector (after Kim et al., 2004).

Voltage V (V)

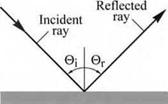
10.4 Specular and diffuse reflectors In specular reflectors, the angle of the reflected light ray is equal to the angle of the incident light ray. Specular reflectors are thus deterministic, i. e. the angle of reflection is pre-determined by the angle of the incident light ray. Diffuse reflectors behave very differently, as shown in Fig. 10.16. The reflected intensity is distributed over a wide range of angles, independent of the incidence angle of the incoming ray. We will next discuss the properties of lambertian sources and lambertian reflectors and subsequently discuss implications for LEDs.

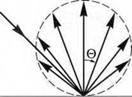
Lambertian surface sources are motivated by the frequently observed experimental fact that the source radiance (i. e. the optical power emitted per steradian per unit surface area of the source) is a constant, independent of the viewing angle. That is, the radiance and luminance of a lambertian source are independent of the viewing angle. The sun is the prime example of a lambertian source. As shown in Fig. 10.17 (a), the sun’s surface has the same brightness (luminance), irrespective of the viewing angle. That is, the brightness (luminance) is the same for, e. g., the normal-incidence viewing angle and an oblique-incidence viewing angle with respect to the sun’s surface. For the same reason, the moon, shown in Fig. 10.17 (b), can be

considered a good example of a lambertian reflector. Light-diffusing reflectors randomize the propagation direction of incoming photons and are referred to as diffuse or lambertian reflectors.

(a) Specular reflector

(b) Diffuse (lambertian) reflector

Fig. 10.16. Schematic of a specular and a diffuse (lambertian) reflector. The re­flected power distribution of a lambertian reflector follows a cos 0 dependence.

We now assume that a lambertian source has an intensity (i. e. optical power emitted per steradian) along the direction given by the angle 0 is given by

(10.31)

I = In cos 0

where In is the intensity emitted normal to the reflector surface. The angular cos 0 dependence of the equation is known as Lambert’s cosine law.

Fig. 10.17. (a) The sun’s surface brightness is independent of viewing angle with respect to the sun’s surface. It is a good example of a lambertian source, (b) The moon is a good example of a lambertian reflector.

Next, we will show that Lambert’s cosine law results in a source luminance (or radiance, in radiometric units) that is independent of the viewing angle with respect to the source surface. Assume a lambertian surface source with area A. The projected area visible to an observer positioned at angle 0 is given by A cos 0. Thus the luminance found by the observer is given by

In A cos 0

Luminance = ------------------------- =---- I n (10.32)

A cos 0

where A cos 0 is the surface area seen by the observer. Thus the luminance is constant, independent of the viewing angle. This fact is corroborated by the photographs shown in Fig. 10.17.

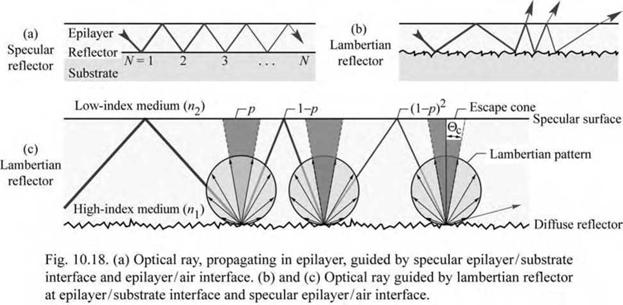
Light propagating in a layer clad by specular reflectors will be waveguided within the layer. However, light propagating in a layer clad by a lambertian reflector can be out-coupled into free space as shown in Fig. 10.18. As a lambertian reflector follows the cos 0 dependence, the probability of reflected light falling into the escape cone defined by the angle 0c is given by

f"c In cos 0 2n sin 0 d0 f c sin 20 d0 ,

J0 n J 0 1 - cos 20c nn-з-зч

p = ;----- . (10 33)

- 90° ^ ^ r 90°

In cos 0 2n sin 0 d0 0 n 0

Using Snell’s law (n1 sin 0c = n2, where n1 is the refractive index of the waveguide and n1 > n2), one obtains

2

(10.34)

= 1 - cos [2arcsin(n2 /nj)]

V n1 J

p = 2

Assuming a lambertian reflector with unit reflectivity (R = 1.0), the light intensity inside the semiconductor decreases according to a geometric series. After N reflection events, the intensity of the light ray will have fallen to (1 - p)N. Defining N as the number of reflection events after

which the light intensity has decreased to 1/e, we can write the equation

(10.35)

(1 - p)N = 1/e.

Solving the equation for N allows one to calculate the average number of reflection events before the light ray will escape into the free space surrounding the semiconductor. One obtains

N

(10.36)

As an example, we consider n1 = 2.5 (GaN) and n2 = 1 (air) and obtain N = 5.7. That is, light escapes from the waveguide after about six diffuse reflection events. Thus the introduction of diffuse reflectors into LED structures is a fruitful strategy in attaining laterally scalable emitters

that do not suffer from an efficiency penalty usually associated with the up-scaling of the LED

chip dimension (Kim et al., 2006).

Mechanical roughening of reflective surfaces generally results in a change from specular to diffuse reflection characteristics. Such reflective surfaces can be, e. g., metallic surfaces or dielectric surfaces. In addition, porous silica (optionally coated with a metal) is known to have diffuse reflection characteristics as multiple refraction, reflection, and scattering events at pore/silica interfaces randomize the photon propagation direction.

1.0 0.8 0.6 0.4 0.2 0.0 0.2 0.4 0.6 0.8 1.0

10° 0° 10°

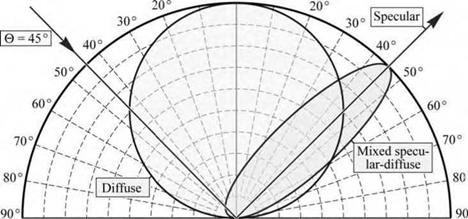
Fig. 10.19. Schematic reflection contour plots of a specular reflector, diffuse reflector, and a mixed specular-diffuse reflector for an angle of incidence of 45°.

i°

о

The fabrication of ideal lambertian reflectors requires substantial roughness (greater than the wavelength of light, X). Such ideal diffuse reflectors would have a reflection characteristic that is

independent of the angle of incidence. Many real surface-textured reflectors have a mixed

specular-diffuse reflection characteristic with a preferential direction along the specular - reflection direction. Figure 10.19 shows the schematic reflection contour plots of a diffuse reflector, a mixed specular-diffuse reflector, and a specular reflector for an angle of incidence of 45°.

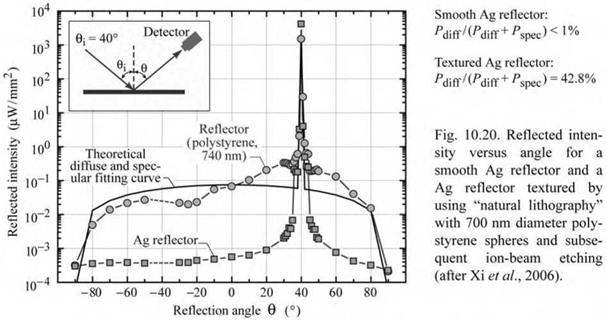
Figure 10.20 shows the measured reflected intensity versus reflection angle for a planar smooth Ag reflector and a surface-textured Ag reflector. The surface roughening was achieved by natural lithography using 700 nm diameter polystyrene spheres on the substrate, followed by ion-beam etching and Ag deposition. Inspection of the figure reveals a strong diffuse background for the textured reflector that is about two orders of magnitude higher than that of the planar Ag reflector. However, the textured reflector still exhibits a specular component. The relative strength of the diffuse and specular components of mixed specular-diffuse reflectors can be assessed quantitatively using the model developed by Xi et al. (2006). Using this model, it is found that the mixed specular-diffuse reflector, shown in Fig. 10.20, has a diffuse power ratio of Pdiff / (Pspec + Pdff) = 42.8%. The root-mean-square (rms) roughness of the partially diffuse reflector shown in Fig. 10.20 is 21.2 nm. By further increasing the rms roughness, diffusive power ratios of 100% can be attained.

Exercise: Lambertian reflectors in LEDs. Assume a lambertian reflector with reflectivity 1.0 that is incorporated in a lossless GaAs LED structure with refractive index of 3.5. Assume that the outside medium is air. Calculate the critical angle of the escape cone, the probability that a reflected light ray falls within the escape cone and the average number of reflection events before a photon escapes from the

Solution: 0C = 16.6°; p = 8.2%; N = 11.7.

Would a hypothetical planar reflector that reflected light coming from any incoming direction towards the surface normal be useful? Is there a physical principle that prevents a reflector from reflecting light in such a way?

Answer: Although such a reflector would be very useful, such a reflector would unfortunately violate the conservation of radiance theorem (previously called the conservation of brightness theorem), which states that it is impossible to increase the radiance of light by a passive optical system beyond a value of L/n2 where L is the radiance in vacuum and n is the refractive index of the medium in which the light propagates.