Carrier temperature and high-energy slope of spectrum
 14 марта, 2014
14 марта, 2014  admin
admin The Boltzmann distribution of carriers, applicable to the high-energy part of the emission spectrum, results in an exponential dependence of the emission intensity on energy, i. e.
I к exp [-hvl(kTc) (6.1)
where Tc is the carrier temperature. The high-energy slope of the spectrum is given by
d(lnI)
-1
|
к |
(6.2)
d(hv)
Thus, the carrier temperature can be directly inferred from the slope. Because the carrier temperature is generally higher than the junction temperature, e. g. due to high-energy injection of carriers into the active region, this method gives an upper limit for the actual junction temperature.
|
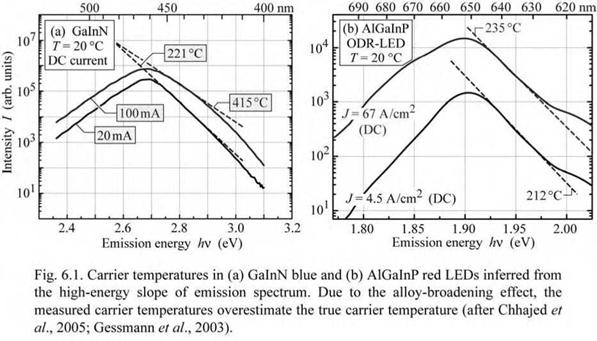
Figure 6.1 shows the evaluation of the carrier temperature from the emission spectrum of a GaInN and an AlGaInP LED (Chhajed et al., 2005; Gessmann et al., 2003). Inspection of the figure reveals that the carrier temperature increases along with the current level. At low current levels, the GaInN device has a carrier temperature of 221 °C and the AlGaInP device has a carrier temperature of 212 °C. At high current levels, the carrier temperature increases to 415 °C and 235 °C for the GaInN and AlGaInP LED, respectively. Due to the alloy-broadening effect occurring in ternary and quaternary semiconductor alloys, these temperatures overestimate the true carrier temperature. |
Semiconductor alloys exhibit substantial broadening of the emission spectrum (and its high- energy slope) due to alloy broadening, i. e. the statistical fluctuation of the chemical composition occurring in ternary and quaternary semiconductors (Schubert et al., 1984). De-convolution of the alloy-broadening effect and the kT-broadening effect allows for a more accurate estimate of the carrier temperature.
The determination of the carrier temperature using the high-energy slope works best for binary compounds such as GaAs or InP. Such semiconductors do not exhibit alloy broadening and thus the high-energy slope is more representative of the true carrier temperature.

 Опубликовано в
Опубликовано в