Из приведенных данных видно, что наиболее существенной операцией при определении деформаций и напряжений как в про­цессе нагрева, так и в про­цессе остывания является на­хождение положения прямой действительных деформаций отдельных волокон полосы при заданных тепловых деформа­циях X, определяемых в пред­положении возможности неза­висимого изменения своей длины каждым волокном по­лосы.

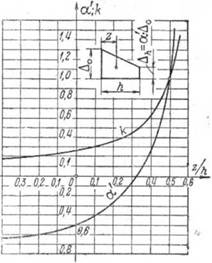
Для упрощения определе­ния положения прямых А при заданных кривых X или X' можно использовать график, представленный на рис. 27.

Основанием для построения графика послужили следую­щие соображения.

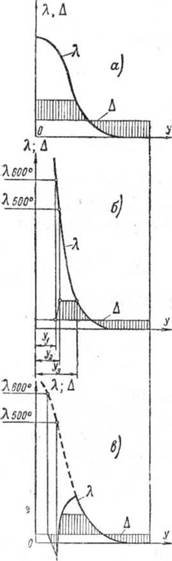
В случае, когда разность Рис. 27. График лля определения

Ад, — Ху| или |Ау—нигде не положения прямой

превышает |е, | (рис. 25, б),

ур-ния (2") для определения положения прямой А

А А

(Ау — х 😉 dy = О и f (Ду — Ху) ydy = О

могут быть переписаны в следующем виде:

Л Л

| у dy = J Д, dy

О О

Л Л

ydy =* f Д^гіу.

о "о

Из последних равенств следует, что площадь Fy ограничен-

h

ная прямой & (F = Дydy), и момент М этой площади огноси-

о

Л

тельно точки О (М — Дyydy) соответственно равны площади Ф,

*о

h

ограниченной кривой X (Ф== ydy) и моменту ЗЯ этой площади

о

Л

(ЭД — ^ Xyydy). Так как площадь кривой X и момент этой пло-

0

щади легко могут быть вычислены (кривая X задана), то положе­ние прямой Д можно определить по площади. Р=Ф и по мо­менту М — ЭД.

Действительно, если ординаты прямой Д в крайних точках равны Д0 и Дл (см. схему на рис. 27), причем

Дл = а'А>

то площадь, ограниченная прямой Д, может быть выражена сле­дующим образом:

f=? bydy = •h‘ — К-h-А„,

о

г* 1 +«'

где К = —.

Положение центра тяжести этой площади относительно точки О определится расстоянием z, которое равно

А

U yydy

М о _ h 1 + 2а'

Z~~ F ~ * ~~ 3 1 +о'

j Д v

о

и, следонательно,

£_ _ JL 1 + 2а'

h З 1 - j - а' "

Таким образом и величина /С и величина -^ зависят от а'. На графике рис. 27 для удобства пользования представлена зави­симость а' и К от - г* и

Величины Д0 и ДА, определяющие положение прямой Д, могут быть найдены следующим образом.

По заданной кривой X вычисляются Ф и ЗЇЇ и определяется

величина 2= ф - и отношение Л-, справедливое и для прямой Д-

(так как Ф = /^ и 2ft ==М). По графику на рис. 27 определяются величины а' и К.

F = K. h.^t F Ф

Учитывая, что

находим

о K-h ~~ K-h

Д

после чего

ДЛ = а Д0.

Подобным же образом может быть определено положение прямой и в случае, представленном на рис. 24, б.

Если задаться значением у3, то из уравнений (2) можно опре - делить площадь Fhy^ ограниченную прямой Д на участке yz-±-hr и момент этой площади Mh,

F 'Уг—Уш—УЖ

= + 1§■ 8Л3^з—у— УЇ—УіУі)-

После определения Fhy и Мну находится величина

Уз

' Мн

Z = -

Так как на графике рис. 27 z означает расстояние центра тяжести площади, ограниченной прямой Дот начальной точки пря­мой, для которой A^ = A0, a h равно полной ширине участка,, ограниченного прямой Д, то в рассматриваемом случае при сдви­нутом относительно начала координат участке, ограниченном*

прямой Д, вместо-Ц-, следует принять

г~Уг h—yz ’

что позволит, пользуясь графиком, определить ДЛ. ^

Ф»+-у«»(*л-л-Л>

А",=" К-(Ь-Уа)

Если оказывается равной Луз = —zs, как того требует

уравнение (2'), то

ДА = а'.Д^

Если К не удовлетворяет уравнению (2'), то необходимо задаться другим значением _у3 и повторить весыюдсчет. Обычно

Рис. 28. Определение деформа­ций неравномерно нагретой за­крепленной полосы.

после двух-трех попыток находится правильное значение у3, а следова­тельно, и положение прямой Д.